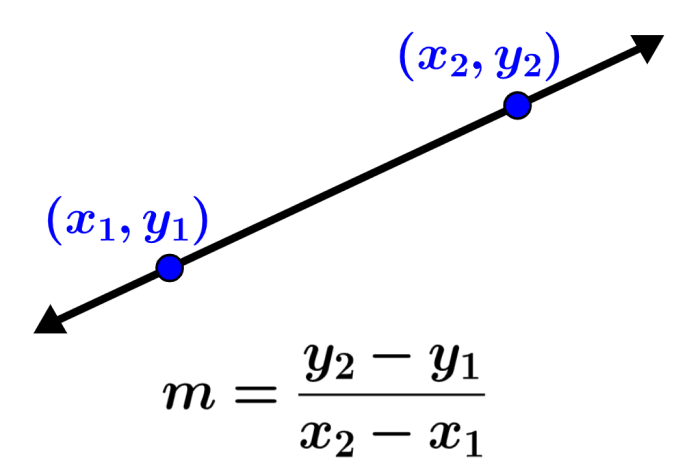
We can calculate the slope of a line using two points that are part of the line. Therefore, we form a fraction, where the numerator corresponds to the change in the y-coordinates of the points and the denominator corresponds to the change in the x-coordinates.
Here, we will learn about the formula that we can apply to calculate the slope using two points. Then, we will apply this formula to solve some problems.
Formula for the slope using two points
We can find the formula for the slope by using the coordinates of two points that are part of the line. The slope equals the change in y divided by the change in x. Therefore, if we have the points $latex A=(x_{1}, y_{1})$ and $latex B = (x_{2}, y_{2})$, the slope formula is:
| Formula for the slope $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ |
Slope of a common lines
Using the slope formula, we can determine the slope of some common lines for reference
Slope of a horizontal line
A horizontal line has no inclination with respect to the x-axis, so its slope is equal to 0. The y coordinates of all points on a horizontal line are the same, so when using the slope formula, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex =\frac{0}{x_{2}-x_{1}}$
$latex m=0$
Slope of a vertical line
A vertical line has an undefined slope. All points on a vertical line have coordinates in x that are the same, so when applying the slope formula, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex =\frac{y_{2}-y_{1}}{0}$
We know that division by 0 is undefined.
Slope of parallel lines
For two or more lines to be parallel, their slopes must be equal. For example, suppose we have the lines $latex l_{1}$ and $latex l_{2}$ with slopes $latex m_{1}$ and $latex m_{2}$ respectively. If these lines are parallel, we must have:
$latex m_{1}=m_{2}$
Slope of perpendicular lines
The slopes of two parallel lines are equal to the negative reciprocal of each other. For example, suppose we have the lines $latex l_{1}$ and $latex l_{2}$ with slopes $latex m_{1}$ and $latex m_{2}$ respectively. If these lines are perpendicular, we must have:
$latex m_{1}=-\frac{1}{m_{2}}$
Examples with answers of slope of a line using two points
The formula for the slope of a line is applied using the two points given to obtain the answer. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
We have a line that contains the points (1, 3) and (3, 7). What is its slope?
Solution
We have the two points:
- $latex (x_{1}, y_{1})=(1, 3)$
- $latex (x_{2}, y_{2})=(3, 7)$
We apply the slope formula with the two given points:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{7-3}{3-1}$
$latex m=\frac{4}{2}$
$latex m=2$
The slope of the line is 2.
EXAMPLE 2
What is the slope of a line that has the points (3, 2) and (8, 3)?
Solution
We have the following coordinates of the points:
- $latex (x_{1}, y_{1})=(3, 2)$
- $latex (x_{2}, y_{2})=(8, 3)$
We use these coordinates in the slope formula and we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{3-2}{8-3}$
$latex m=\frac{1}{5}$
The slope of the line is $latex \frac{1}{5}$.
EXAMPLE 3
The points (-1, 3) and (6, -4) are part of a line. What is its slope?
Solution
We have the following points:
- $latex (x_{1}, y_{1})=(-1, 3)$
- $latex (x_{2}, y_{2})=(6, -4)$
When we apply the slope formula with these coordinates, we have:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-4-3}{6-(-1)}$
$latex m=\frac{-7}{7}$
$latex m=-1$
The slope of the line is $latex -1$.
EXAMPLE 4
What is the slope of a line that contains the points (-3, -2) and (3, -5)?
Solution
We can write as follows:
- $latex (x_{1}, y_{1})=(-3, -2)$
- $latex (x_{2}, y_{2})=(3, -5)$
We use the slope formula with the given coordinates:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{-5-(-2)}{3-(-3)}$
$latex m=\frac{-3}{6}$
$latex m=-\frac{1}{2}$
The slope of the line is $latex -\frac{1}{2}$.
Slope of a line using two points – Practice problems
Solve the following practice problems using the slope formula with the given points. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about the midpoint, slope, and distance on the plane? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
