Adjacent angles are angles that have a common vertex and a common side but do not overlap. Recall that a vertex is a point where two segments or two sides of an angle meet and the sides are simply the line segments that contain the angle. A common example of adjacent angles is the interior angles of a polygon. Any pair of interior angles that share one side in a polygon are called adjacent interior angles.
Here, we will look at a more detailed definition of these types of angles along with diagrams to illustrate these concepts. Also, we will learn about the most important properties of adjacent angles and we will look at some examples.
What are adjacent angles?
Adjacent angles are angles that share a common vertex and a common side. The point where two sides meet and the angle is located is called the vertex. Adjacent angles can be complementary or supplementary if these angles share a vertex and a side.
Let us consider the following angles. The green angle is formed by the segments OA and OC and is represented as ∠AOC. The pink angle is formed by the segments OC and OB and is represented as ∠COB. This pair of angles are located close to each other and are considered adjacent.
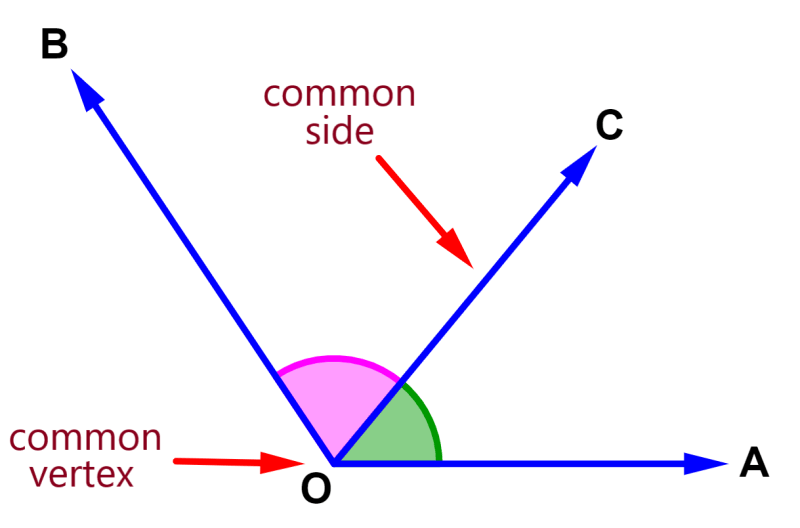
These angles are adjacent since they have a common vertex, the vertex O. In addition, the angles also have a common side, the OC side.
Properties of adjacent angles
The following are some of the important properties of adjacent angles:
- Adjacent angles share a common vertex.
- These angles share a common side.
- The angles do not overlap.
- These angles do not have a common interior point.
- Adjacent angles can be complementary or supplementary.
- These angles have a non-common side on both sides of the common side.
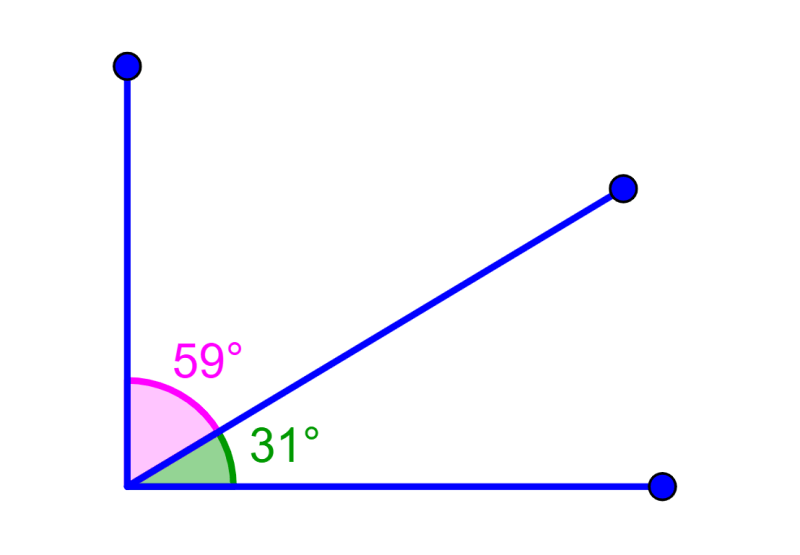
Adjacent complementary angles
We know that adjacent angles share a vertex and one side. Recall that if two angles add up to 90°, these angles are called complementary angles. Therefore, the adjacent complementary angles are angles that share a vertex and a side and add up to 90°.
The following diagram shows an example of adjacent complementary angles.
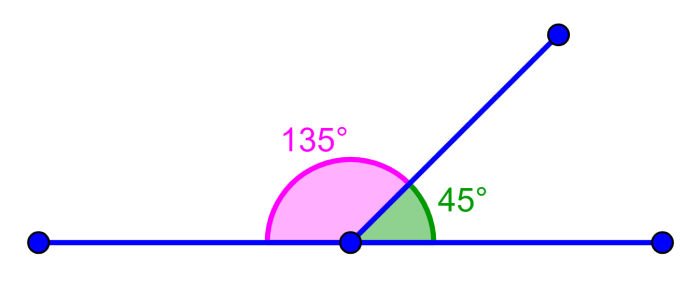
Adjacent supplementary angles
These types of angles meet the conditions of supplementary angles and adjacent angles at the same time. Adjacent angles are characterized by having a common vertex and a common side. On the other hand, supplementary angles are characterized by being a pair of angles that have a sum equal to 180°.
The following is an example of adjacent supplementary angles.
Adjacent angles – Examples with answers
EXAMPLE 1
Which of the following angles are adjacent?
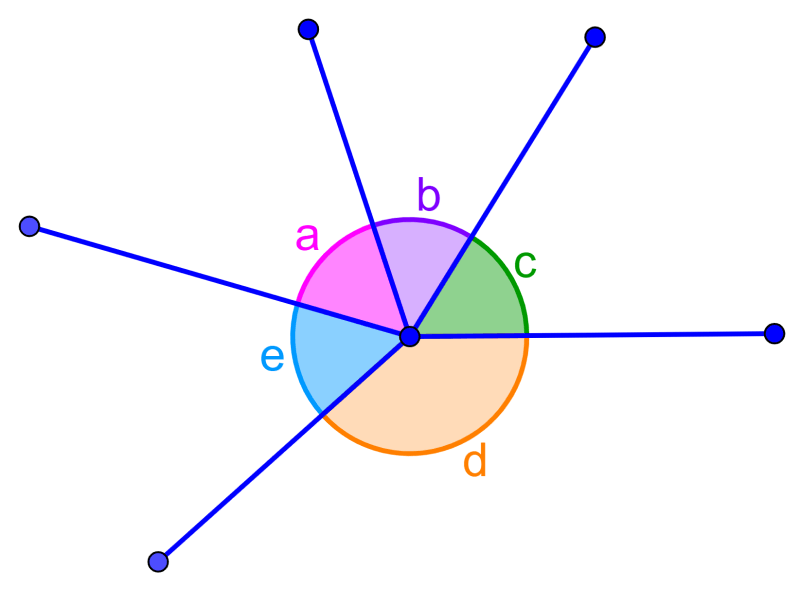
Solution: The following angles are adjacent:
- a and b
- b and c
- c and d
- d and e
- e and a
EXAMPLE 2
The following angles are adjacent complementary. What is the measure of angle α?
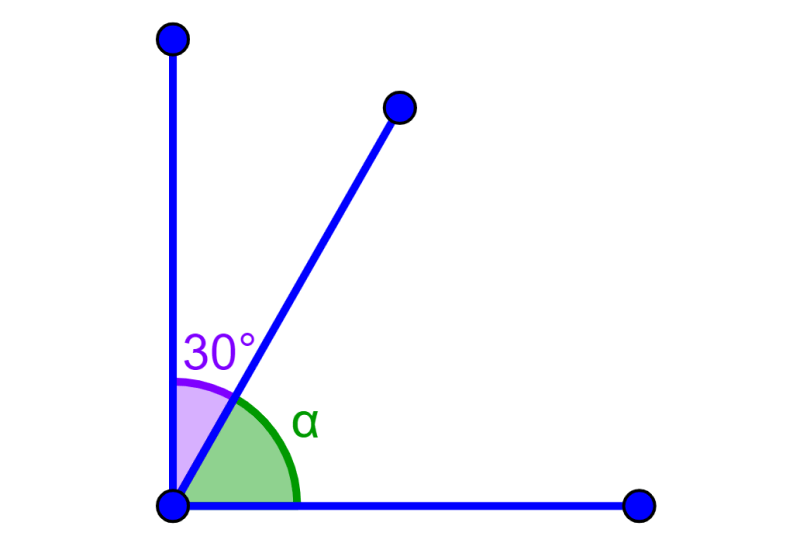
Solution: We know that the complementary angles add up to 90°. Therefore, we have:
α=90°-30°
α=60°
EXAMPLE 3
If the following angles are adjacent supplementary, what is the measure of angle β?
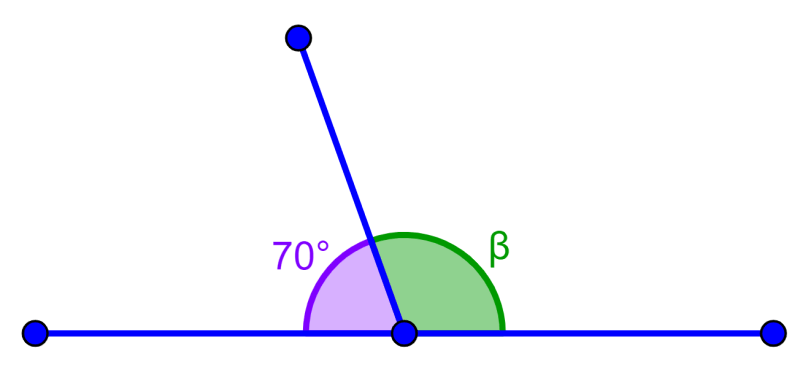
Solution: Supplementary angles add up to 180°. Therefore, we have:
β=180°-70°
β=110°
See also
Interested in learning more about the inscribed angle theorem and other angles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
