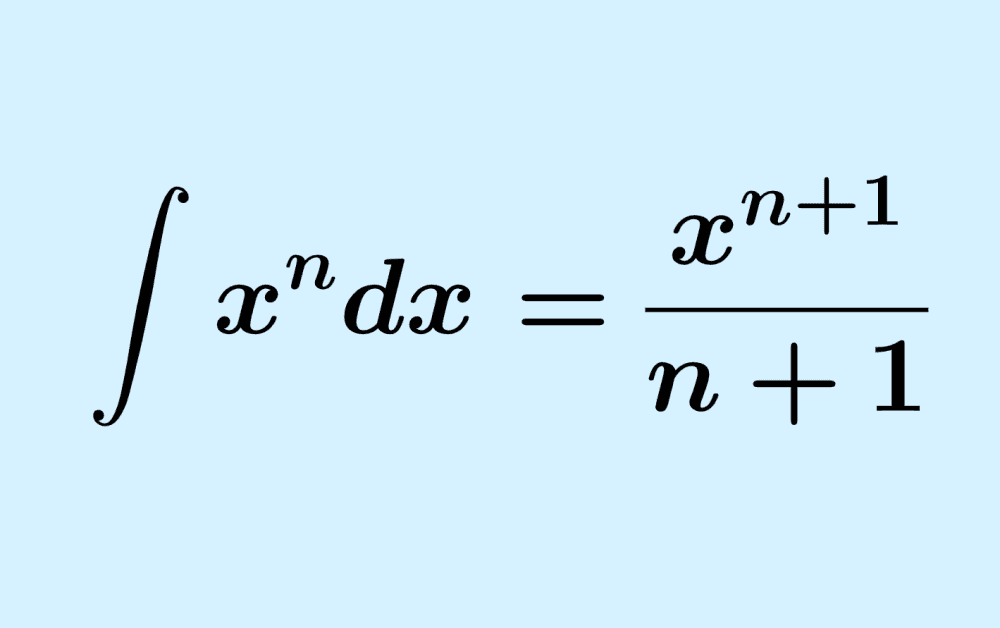The integral of a polynomial can be found by adding 1 to the exponents of the variable of each term of the polynomial. Then, we multiply each term by the reciprocal of the new exponent. Finally, we simplify the expression obtained and add the constant of integration.
Here, we will learn how to find integrals of polynomials. We will explore 10 examples with answers on integrals of polynomials. Then you can put your skills to the test with a few practice problems.
Process used to find the integral of a polynomial function
To find the integral of a polynomial function, we use a reverse process to that used to differentiate a polynomial.
For example, suppose we want to find the integral of $latex \int x^4 dx$. For this, we observe that the derivative of $latex x^5$ is equal to $latex 5x^4$ and we would have the same power of x.
However, in this case we don’t need the constant 5, so we multiply $latex x^5$ by $latex \frac{1}{5}$. Then, we have
The derivative of $latex \frac{1}{5} x^5$ is $latex x^4$
Therefore,
$$\int x^4 dx =\frac{1}{5}x^5+c$$
In general, we have the following formula:
$$\int ax^n dx =\frac{ax^{n+1}}{n+1}+c$$
where, $latex n \neq -1$.
We can use the following steps to find the integral of any polynomial:
Step 1: Add 1 to the exponents of each term of the polynomial.
Note: Constant terms are equivalent to having the variable $latex x^0$, so adding 1 gives us $latex x^1=x$.
Step 2: Multiply each term by the reciprocal of the new exponent.
Note: The reciprocal of a number is equal to 1 over a number. For example, the reciprocal of 5 is $latex \frac{1}{5}$.
Step 3: Simplify the resulting integral and add the constant term $latex c$.
Integrals of Polynomials – Examples with answers
EXAMPLE 1
Find the integral of the polynomial $latex 3x^2+1$
Solution
To solve this exercise, we have to start by forming the integral with the given polynomial:
$latex \int 3x^2+1 dx$
Now, we can get the integral by considering the following:
- The exponent of each variable to be integrated has to be added 1.
- Each term of the polynomial must be divided by the new exponent.
Applying this, we have:
$$\int 3x^2+1 dx=\frac{3x^3}{3}+1x$$
Simplifying and adding the constant of integration, we have:
$$\int 3x^2+1 dx=x^3+x+c$$
EXAMPLE 2
What is the integral of the polynomial $latex x^3+2x$?
Solution
We start by forming the integral with the given polynomial:
$latex \int x^3+2x dx$
Now, we can solve the integral of the polynomial by following the steps below.
- We add 1 to the exponent of each term.
- Each term must be divided by the new exponent.
Therefore, we have:
$$\int x^3+2x dx=\frac{x^4}{4}+\frac{2x^2}{2}$$
When we simplify and add the constant of integration, we have:
$$\int x^3+2x dx=\frac{x^4}{4}+x^2+c$$
EXAMPLE 3
Determine the integral of the polynomial function $latex f(x)=-x^3-3x^2$.
Solution
Forming the integral with the given polynomial function, we have:
$latex \int -x^3-3x^2 dx$
Now, we apply the following:
- Each exponent of the variable to be integrated must be added by 1.
- Each term must be divided by the value of the new exponent.
Then, we have:
$$\int -x^3-3x^2 dx=-\frac{x^4}{4}-\frac{3x^3}{3}$$
When we simplify and add the constant of integration, we get:
$$\int -x^3-3x^2 dx=-\frac{x^4}{4}-x^3+c$$
EXAMPLE 4
What is the integral of the polynomial function $latex f(x)=5x^3-3x-2$?
Solution
The integral to be evaluated is:
$latex \int 5x^3-3x -2 dx$
We solve the integral using the following steps:
- We add 1 to the exponent of each term of the polynomial.
- We divide each term by the new exponent.
Applying this, we have:
$$\int 5x^3-3x -2 dx=\frac{5x^4}{4}-\frac{3x^2}{2}-2x$$
Simplifying and adding the constant of integration, we have:
$$\int 5x^3-3x -2 dx=\frac{5x^4}{4}-\frac{3x^2}{2}-2x+c$$
EXAMPLE 5
Find the integral of the polynomial $latex 2x^3-6x^2+5x$.
Solution
Forming the integral to be evaluated, we have:
$latex \int 2x^3-6x^2+5x dx$
Now, we can apply the following to solve the integral:
- The exponent of x of each term must be added 1.
- Each term must be divided by the value of the new exponent.
When we apply this, we have:
$$\int 2x^3-6x^2+5x dx=\frac{2x^4}{4}-\frac{6x^3}{3}+\frac{5x^2}{2}$$
When we simplify and add the constant of integration, we have:
$$\int 2x^3-6x^2+5x dx=\frac{x^4}{2}-2x^3+\frac{5x^2}{2}+c$$
EXAMPLE 6
If we have the function $latex f(x)=2x^4+3x^3-2x^2$, what is its integral?
Solution
The integral to be evaluated is:
$latex \int 2x^4+3x^3-2x^2 dx$
When we evaluate this integral, we have:
$$\int 2x^4+3x^3-2x^2 dx=\frac{2x^5}{5}+\frac{3x^4}{4}-\frac{2x^3}{3}$$
Simplifying and adding the constant of integration, we have:
$$\int 2x^4+3x^3-2x^2 dx=\frac{2x^5}{5}+\frac{3x^4}{4}-\frac{2x^3}{3}+c$$
EXAMPLE 7
Find the integral of the function $latex f(x)=3x^3+(x-2)^2$.
Solution
We can start by expanding the binomial and simplifying the given polynomial function:
$latex f(x)=3x^3+(x-2)^2$
$latex f(x)=3x^3+x^2-4x+4$
Forming the integral, we have:
$latex \int 3x^3+x^2-4x+4 dx$
Solving the integral, we have:
$$\int 3x^3+x^2-4x+4 dx=\frac{3x^4}{4}+\frac{x^3}{3}-\frac{4x^2}{2}+4x$$
When we simplify and add the constant of integration, we have:
$$\int 3x^3+x^2-4x+4 dx=\frac{3x^4}{4}+\frac{x^3}{3}-2x^2+4x+c$$
EXAMPLE 8
Find the integral of $latex f(x)=2x^3+(x+4)^2-2x^2$.
Solution
Expanding the given polynomial and simplifying, we have:
$latex f(x)=2x^3+(x+4)^2-2x^2$
$latex f(x)=2x^3+x^2+8x+16-2x^2$
$latex f(x)=2x^3-x^2+8x+16$
The integral to be evaluated is:
$latex \int 2x^3-x^2+8x+16 dx$
Therefore, we have:
$$\int 2x^3-x^2+8x+16 dx=\frac{2x^4}{4}-\frac{x^3}{3}+\frac{8x^2}{2}+16x$$
Simplifying and adding the constant of integration, we have:
$$\int 2x^3-x^2+8x+16 dx=\frac{x^4}{2}-\frac{x^3}{3}+4x^2+16x+c$$
EXAMPLE 9
If the derivative of a curve is $latex g(x)=4x^3-2$ and the curve passes through the point $latex (-1, ~2)$. Find the equation of the curve.
Solution
In this problem, we need to find the function of the curve that has a derivative equal to $latex g(x)=4x^3-2$. That is, we have to find the integral of the given derivative.
Then, forming the integral to be evaluated, we have:
$latex \int 4x^3-2 dx$
Solving this, we have:
$$\int 4x^3-2 dx=\frac{1}{4}4x^4-2x+c$$
$$\int 4x^3-2 dx=x^4-2x+c$$
We can determine the value of the constant of integration by using the point $latex (-1, ~2)$. Then, we have:
$latex y=x^4-2x+c$
$latex 2=(-1)^4-2(-1)+c$
$latex 2=1+2+c$
$latex c=-1$
Thus, the equation of the curve is $latex y=x^4-2x-1$.
EXAMPLE 10
A curve has a slope represented by $latex 20x^4-10x$. If the curve passes through the point (1, 3), what is its equation?
Solution
In this case, we know the equation of the slope of the curve. However, we remember that the slope is equal to the derivative of the function.
Similar to the previous example, we are going to find the integral of $latex 20x^4-10x$, since the integral represents the equation of the curve:
$latex \int 20x^4-10x dx$
Solving this integral, we have:
$$\int 20x^4-10x dx=\frac{20x^5}{5}-\frac{10x^2}{2}+c$$
$$\int 20x^4-10x dx=4x^5-5x^2+c$$
If we use the point (1, 3), we can determine the value of the constant:
$latex y=4x^5-5x^2+c$
$latex 3=4(1)^5-5(1)^2+c$
$latex 3=4-5+c$
$latex c=4$
Thus, the equation of the curve is $latex y=4x^5-5x^2+4$.
Integrals of polynomials – Practice problems
If we have $latex F(x)=\int f(x)dx$, find the value of $latex F(2)$ if $latex c=0$ for the function: $$f(x)=4x^3+6x^2-5x-10$$
Write the answer in the input box
See also
Interested in learning more about integrals of functions? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
