The natural logarithm of x squared, also denoted as ln(x2), is the logarithm of x2 to base e (euler’s number). The derivative of the natural logarithm of x2 is equal to two over x, 2/x. We can prove this derivative using the chain rule or implicit differentiation.
In this article, we will see how to find the derivative of the natural logarithm of x squared. We will see proofs, graphical comparisons of the original function and its derivative, and some examples.
CALCULUS
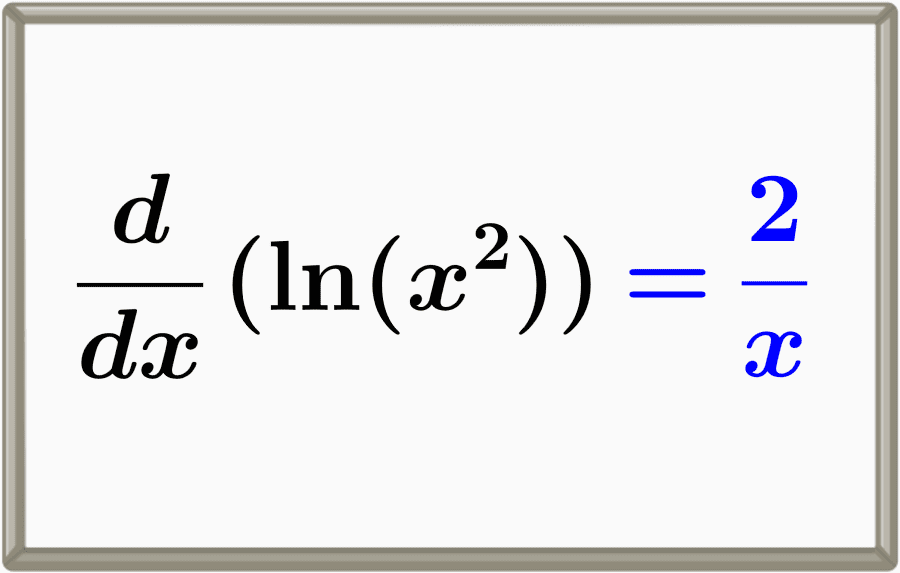
Relevant for…
Learning how to find the derivative of the natural logarithm of x squared.
CALCULUS
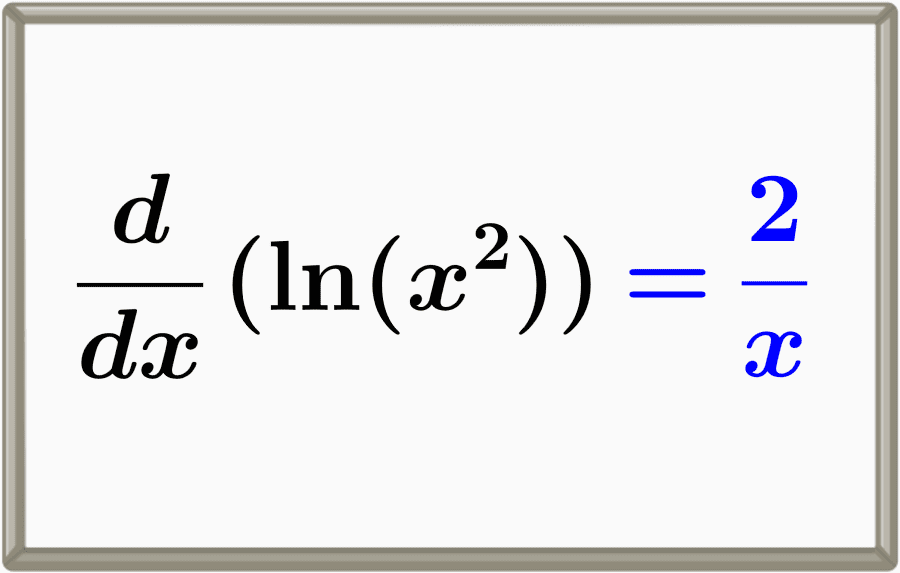
Relevant for…
Learning how to find the derivative of the natural logarithm of x squared.
Proofs of the Derivative of Natural Logarithm of x^2
Listed below are the proofs of the derivative of \(\ln{\left(x^2\right)}\). These proofs can also serve as the main methods of deriving this function.
Proof of the derivative of \(\ln{\left(x^2\right)}\) using the Chain Rule Formula
Given that this is a composed function, the chain rule formula can be used to prove the derivative formula for the natural log of \(x^2\). In the composite function \(\ln{\left(x^2\right)}\), the natural logarithmic function will be the outer function f(u), while the \(x^2\) will be the inner function g(x).
As a prerequisite for this topic, please review the chain rule formula by looking at this article: Chain Rule of derivatives. You may also check out this article for the proof of the derivative of natural logarithm using the first principle: Derivative of Natural log (ln(x)).
Let’s have the derivative of the function
$$ F(x) = \ln{\left(x^2\right)}$$
We can determine the two functions that comprise F(x). In this instance, there is a natural logarithmic function and a monomial. We may configure the outer function as follows:
$$ f(u) = \ln{(u)}$$
where
$$ u = x^2$$
Setting the monomial \(x^2\) as the inner function of f(u) by denoting it as g(x), we have
$$ f(u) = f(g(x))$$
$$ g(x) = x^2$$
$$ u = g(x)$$
Deriving the outer function f(u) using the derivative of natural log in terms of u, we have
$$ f(u) = \ln{(u)}$$
$$ f'(u) = \frac{1}{u}$$
Deriving the inner function g(x) using power rule since it is a monomial, we have
$$ g(x) = x^2$$
$$ g'(x) = 2x$$
Algebraically multiplying the derivative of outer function $latex f'(u)$ by the derivative of inner function $latex g'(x)$, we have
$$ \frac{dy}{dx} = f'(u) \cdot g'(x)$$
$$ \frac{dy}{dx} = \left(\frac{1}{u} \right) \cdot (2x)$$
Substituting u into f'(u) and simplifying, we have
$$ \frac{dy}{dx} = \left(\frac{1}{\left(x^2\right)} \right) \cdot (2x)$$
$$ \frac{dy}{dx} = \frac{2x}{x^2}$$
$$ \frac{dy}{dx} = \frac{2}{x}$$
As a result, we arrive at the \(\ln{\left(x^2\right)}\) derivative formula.
$$ \frac{d}{dx} \ln{\left(x^2\right)} = \frac{2}{x}$$
Proof of the derivative of \(\ln{\left(x^2\right)}\) using implicit differentiation
In this proof, you are hereby recommended to learn/review the derivatives of exponential functions and implicit differentiation.
Suppose we have the equation
$$ y = \ln{\left(x^2\right)}$$
In general logarithmic form, it is
$$ \log_{e}{x^2} = y$$
And in exponential form, it is
$$ e^y = x^2$$
Implicitly deriving the exponential form in terms of x, we have
$$ e^y = x^2$$
$$ \frac{d}{dx} (e^y) = \frac{d}{dx} (x^2) $$
$$ e^y \cdot \frac{dy}{dx} = 2x $$
Isolating \( \frac{dy}{dx} \), we have
$$ \frac{dy}{dx} = \frac{2x}{e^y} $$
We recall that in the beginning, \( y = \ln{\left(x^2\right)} \). Substituting this to the y of our derivative, we have
$$ \frac{dy}{dx} = \frac{2x}{e^{\left(\ln{\left(x^2\right)}\right)}} $$
Simplifying and applying a property of logarithm, we have
$$ \frac{dy}{dx} = \frac{2x}{x^2} $$
$$ \frac{dy}{dx} = \frac{2}{x} $$
Evaluating, we now have the derivative of \( y = \ln{\left(x^2\right)} \)
$$ y’ = \frac{2}{x} $$
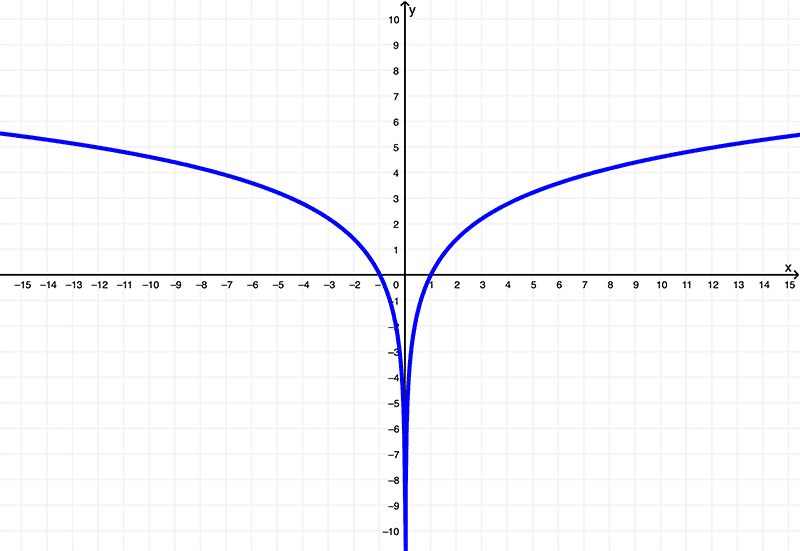
Graph of ln(x^2) vs. its derivative
The graph of the function
$$ f(x) = \ln{\left(x^2\right)}$$
is
And as we know by now, by deriving \(f(x) = \ln{\left(x^2\right)}\), we get
$$ f'(x) = \frac{2}{x}$$
which is illustrated graphically as
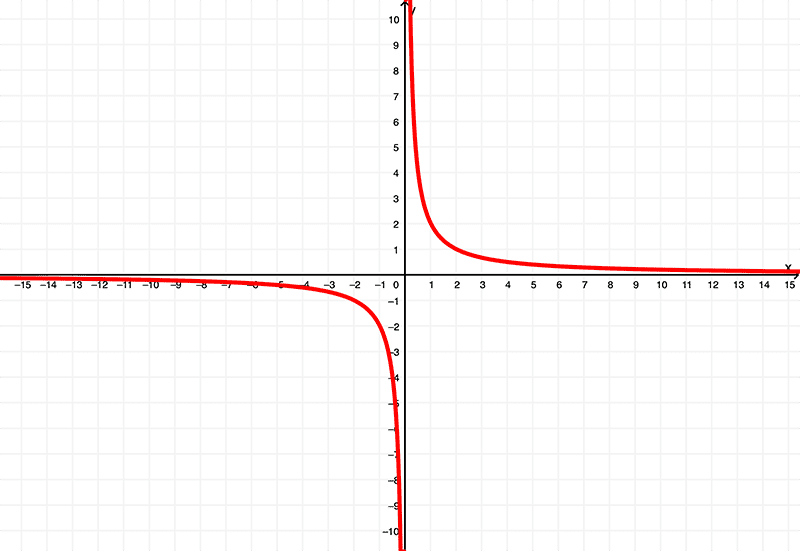
Comparing the graphs, we have

Using these graphs, you can see that the original function (f(x) = \ln(x^2) has a domain of
\( (-\infty,0) \cup (0,\infty) \) or \( x | x \neq 0 \)
and exists within the range of
\( (-\infty, \infty) \) or all real numbers
whereas the derivative \(f'(x) = \frac{2}{x}\) has a domain of
\( (-\infty,0) \cup (0,\infty) \) or \( x | x \neq 0 \)
and exists within the range of
\( (-\infty,0) \cup (0,\infty) \) or \( y | y \neq 0 \)
See also
Interested in learning more about the derivatives of logarithmic functions? Take a look at these pages:



