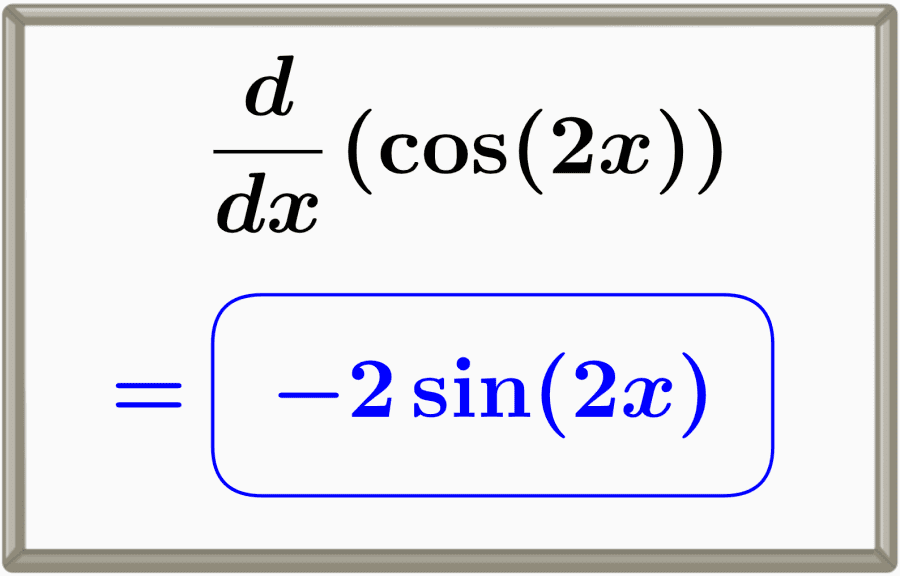The derivative of a cosine function of double angles results in a composite function. The derivative of the cosine of 2x is equal to minus two sine of 2x, -2sin(2x). This derivative can be found using the chain rule and the derivative of cosine.
In this article, we will see how to find the derivative of the composite function cosine of double angles. We’ll cover a proof and graphical comparison of cos(2x) and its derivative.
Proof of The Derivative of The Cosine of Double Angles Using Chain Rule
Because it is a composite function, the chain rule formula is used as the foundation to derive the cosine of a double angle. The trigonometric function cosine will be the outer function f(u) in the composite function cos(2x), whilst the monomial 2x will be the inner function g(x).
As a precondition for this topic, you should review the chain rule formula by visiting this article: Chain Rule of derivatives. In addition, you can visit this article for proof of cosine function derivative: Derivative of Cosine, cos(x).
Suppose we are asked to get the derivative of
$latex F(x) = \cos{(2x)}$
We can identify the two functions that make up F(x). There is a trigonometric function cosine and a monomial in this scenario. It is evident that the given cosine function is the outer function, while the monomial 2x is the inner function. We can set the outer function as
$latex f(u) = \cos{(u)}$
where
$latex u = 2x$
Setting the monomial 2x as the inner function of f(u) by denoting it as g(x), we have
$latex f(u) = f(g(x))$
$latex g(x) = 2x$
$latex u = g(x)$
Deriving the outer function f(u) using the derivative of cosine in terms of u, we have
$latex f(u) = \cos{(u)}$
$latex f'(u) = -\sin{(u)}$
Deriving the inner function g(x) using power rule since it is a monomial, we have
$latex g(x) = 2x$
$latex g'(x) = 2$
Algebraically multiplying the derivative of outer function $latex f'(u)$ by the derivative of inner function $latex g'(x)$, we have
$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$
$latex \frac{dy}{dx} = (-\sin{(u)}) \cdot (2)$
Substituting u into f'(u), we have
$latex \frac{dy}{dx} = (-\sin{(u)}) \cdot (2)$
$latex \frac{dy}{dx} = – (\sin{(2x)} \cdot (2))$
$latex \frac{dy}{dx} = – ((2) \cdot \sin{(2x)})$
In this case, we prefer not to apply the double angle trigonometric identity for cosine as it will make the derivative formula less simplified. Therefore, this gets us to the cos(2x) derivative formula
$latex \frac{d}{dx} \cos{(2x)} = -2\sin{(2x)}$
Graph of cos(2x) VS. its derivative
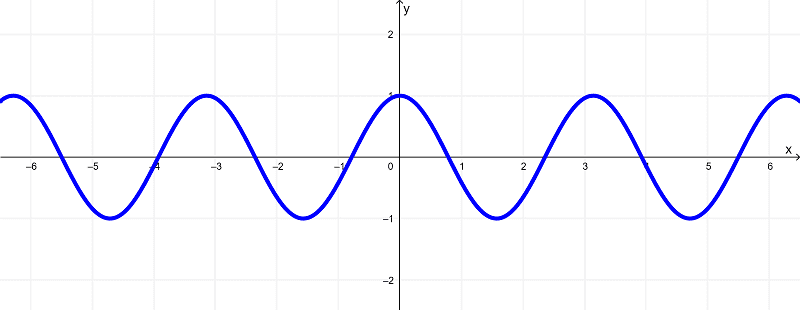
Given the function
$latex f(x) = \cos{(2x)}$
its graph is shown as
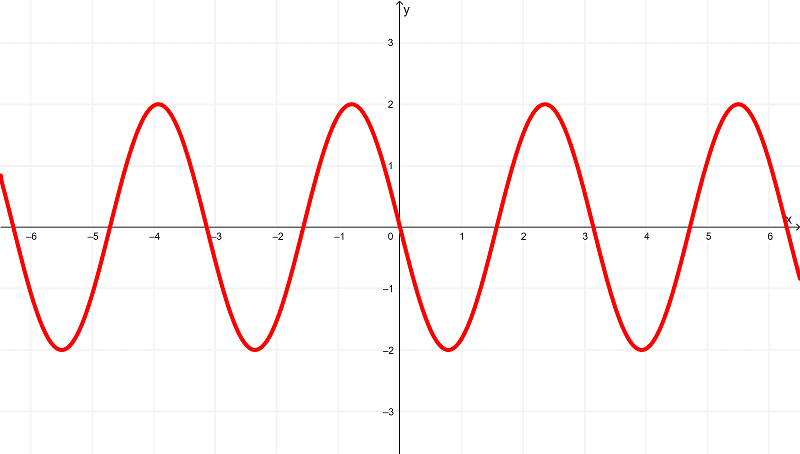
And as we know by now, by deriving $latex f(x) = \cos{(2x)}$, we get
$latex f'(x) = -2\sin{(2x)}$
which if graphed, is shown as
Illustrating both graphs in one, we have
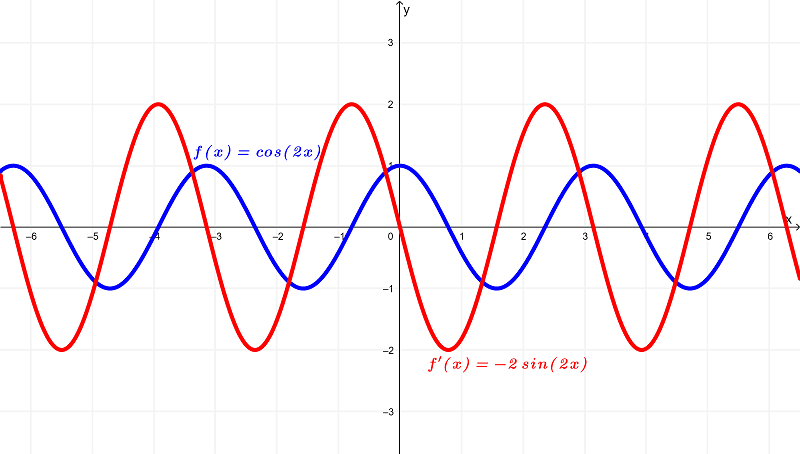
Looking at the differences between these functions based on those graphs, you can see that the original function $latex f(x) = \cos{(2x)}$ has a domain of
$latex (-\infty,\infty)$ or all real numbers
and exists within the range of
$latex [-1,1]$
whereas the derivative $latex f'(x) = -2\sin{(2x)}$ has a domain of
$latex (-\infty,\infty)$ or all real numbers
and exists within the range of
$latex [-2,2]$
Graph Comparison between cos(2x) and cos(x) as well as their derivatives
The graphs shown below illustrates the difference between $latex \cos{(2x)}$ and $latex \cos{(x)}$
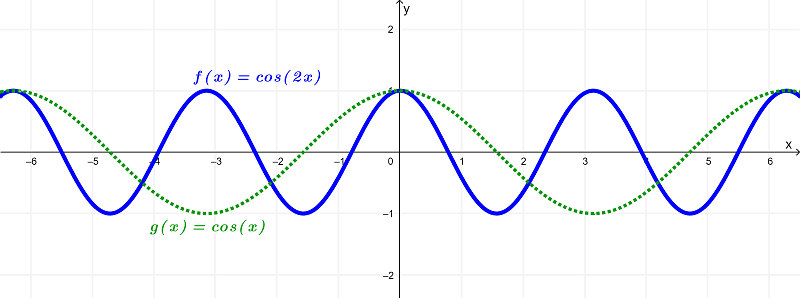
and in terms of their derivatives
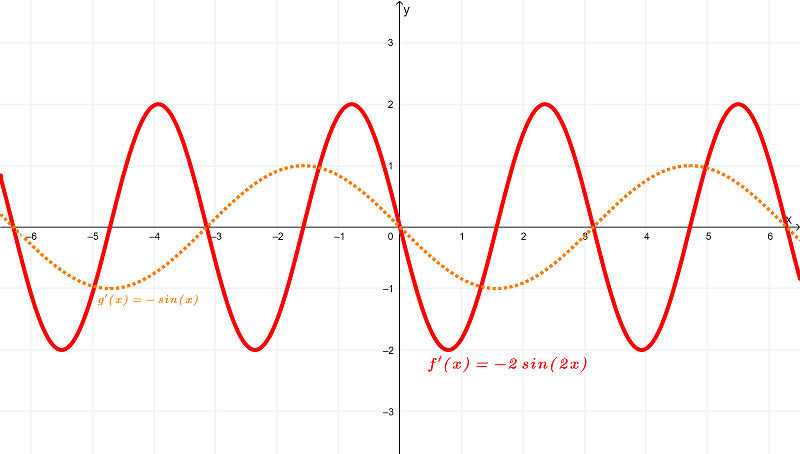
See also
Interested in learning more about the derivatives of trigonometric functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
