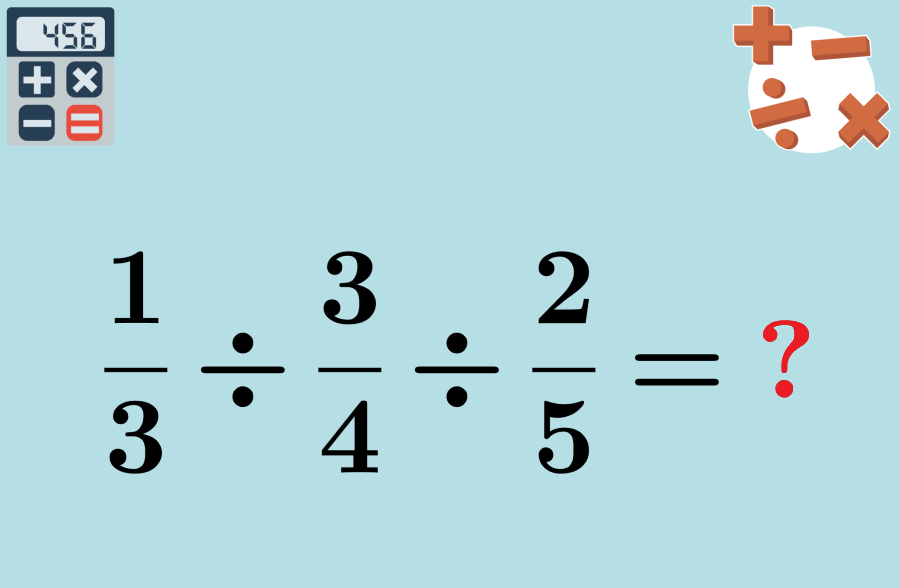10 Examples of Division of Fractions with Answers

To divide two fractions, we have to find the reciprocal of the dividing fraction and write the division as multiplication.

Therefore, considering that the reciprocal of $latex \frac{2}{3}$ is $latex \frac{3}{2}$, we have:

$$\frac{4}{5}\div \frac{2}{3}$$

$$=\frac{4}{5}\times \frac{3}{2}$$

Now, we solve the multiplication by writing as follows:

$$=\frac{4 \times 3}{5 \times 2}$$

Simplifying the 4 in the numerator with the 2 in the denominator, we have:

$$=\frac{2 \times 3}{5 \times 1}$$

Solving the multiplication, we have:

$$=\frac{6}{5}$$

We can simplify by writing as a mixed number:

$$=1\frac{1}{5}$$

The reciprocal of $latex \frac{3}{2}$ is $latex \frac{2}{3}$. Then, we can write the division of fractions as multiplication:

$$\frac{5}{7}\div \frac{3}{2}$$

$$=\frac{5}{7}\times \frac{2}{3}$$

Now, we write the multiplication as follows:

$$=\frac{5 \times 2}{7 \times 3}$$

Solving the multiplications in the numerator and denominator, we have:

$$=\frac{10}{21}$$

The fraction is already simplified.

The reciprocal of $latex \frac{4}{5}$ is $latex \frac{5}{4}$. Then, we use that reciprocal to write the division as multiplication:

$$\frac{8}{9}\div \frac{4}{5}$$

$$=\frac{8}{9}\times \frac{5}{4}$$

Now, we can write as follows:

$$=\frac{8 \times 5}{9 \times 4}$$

We can simplify the 8 in the numerator with the 4 in the denominator:

$$=\frac{2 \times 5}{9 \times 1}$$

Solving the multiplication, we have:

$$=\frac{10}{9}$$

Writing as a mixed number, we have:

$$=1\frac{1}{9}$$

Considering that the reciprocal of $latex \frac{4}{7}$ is $latex \frac{7}{5}$, we can write it as follows:

$$\frac{9}{11}\div \frac{4}{7}$$

$$=\frac{9}{11}\times \frac{7}{4}$$

Now, we write the multiplication like this:

$$=\frac{9 \times 7}{11 \times 4}$$

Solving the multiplications in the numerator and denominator, we have:

$$=\frac{63}{44}$$

We can simplify by writing as a mixed number:

$$=1\frac{19}{44}$$

In this case, we have an integer in the division. We can solve this problem by writing the whole number as a fraction. Therefore, we have:

$$\frac{2}{3}\div \frac{1}{4} \div 2$$

$$=\frac{2}{3}\div \frac{1}{4} \div \frac{2}{1}$$

Now, we convert the divisions to multiplication by taking the reciprocal of the dividing fractions:

$$=\frac{2}{3}\times \frac{4}{1}\times \frac{1}{2}$$

We can write the multiplication as follows:

$$=\frac{2 \times 4 \times 1}{3 \times 1 \times 2}$$

Simplifying the 2 in the numerator with the 2 in the denominator, we have:

$$=\frac{1 \times 4 \times 1}{3 \times 1 \times 1}$$

Solving the multiplication, we have:

$$=\frac{4}{3}$$

Writing as a mixed number, we have:

$$=1\frac{1}{3}$$

Here, we have a mixed fraction. To solve the division, we have to start by converting the mixed fraction to an improper fraction. Therefore, we have:

$$1\frac{3}{4}\div \frac{2}{5}$$

$$=\frac{7}{4}\div \frac{2}{5}$$

Writing multiplication as division, we have:

$$=\frac{7}{4}\times \frac{5}{2}$$

Now, we solve the multiplication by writing as follows:

$$=\frac{7 \times 5}{4 \times 2}$$

$$=\frac{35}{8}$$

Writing as a mixed number, we have:

$$=4\frac{3}{8}$$

We start by converting both mixed fractions to improper fractions. Therefore, we have:

$$2\frac{2}{3}\div 1\frac{3}{4}$$

$$=\frac{8}{3}\div \frac{7}{4}$$

Writing the division as multiplication, we have:

$$\frac{8}{3}\div \frac{7}{4}$$

$$=\frac{8}{3}\times \frac{4}{7}$$

We solve the multiplication as follows:

$$=\frac{8 \times 4}{3 \times 7}$$

$$=\frac{32}{21}$$

We can simplify by writing as a mixed number:

$$=1\frac{11}{21}$$

In this case, we have a division of three fractions, but the process used is the same. Therefore, we write division as multiplication:

$$\frac{3}{5}\div \frac{3}{4}\div \frac{1}{2}$$

$$=\frac{3}{5}\times \frac{4}{3}\times \frac{2}{1}$$

Now, we solve the multiplication by writing as follows:

$$=\frac{3 \times 4 \times 2}{5 \times 3 \times 1}$$

Simplifying the 3 in the numerator with the 3 in the denominator, we have:

$$=\frac{1 \times 4 \times 2}{5 \times 1 \times 1}$$

Solving the multiplications of the numerator and the denominator, we have:

$$=\frac{8}{5}$$

We can simplify by writing as a mixed number:

$$=1\frac{3}{5}$$

We use the reciprocals of the divisor fractions to write division as multiplication:

$$\frac{6}{7}\div \frac{5}{3}\div \frac{3}{4}$$

$$=\frac{6}{7}\times \frac{3}{5} \times \frac{4}{3}$$

We write multiplication as follows:

$$=\frac{6 \times 3 \times 4}{7 \times 5 \times 3}$$

Simplifying the 3 in the numerator with the 3 in the denominator, we have:

$$=\frac{6 \times 1 \times 4}{7 \times 5 \times 1}$$

Solving the multiplications of the numerator and the denominator, we have:

$$=\frac{24}{35}$$

We start by converting the mixed fractions to improper fractions:

$$2\frac{3}{4}\div 1\frac{2}{3}\div 1\frac{4}{5}$$

$$=\frac{11}{4}\div \frac{5}{3}\div \frac{9}{5}$$

Writing division as multiplication, we have:

$$=\frac{11}{4}\times \frac{3}{5}\times \frac{5}{9}$$

Now, we solve the multiplication by writing as follows:

$$=\frac{11 \times 3 \times 5}{4 \times 5 \times 9}$$

We can simplify the 5 in the numerator with the 5 in the denominator and the 3 in the numerator with the 9 in the denominator:

$$=\frac{11 \times 1 \times 1}{4 \times 1 \times 3}$$

Solving the multiplication, we have:

$$=\frac{11}{12}$$