The multiplicity of roots refers to the number of times each root appears in a given polynomial. Determining the multiplicity of the roots of polynomials is easy if we have the factored version of the polynomial. Alternatively, it is also possible to determine the multiplicity of the roots by looking at the graph of the polynomial.
Here, we will learn about the multiplicity of roots and learn how to determine the multiplicity of roots algebraically. In addition, we will also learn to find the multiplicity of roots using the graphs of polynomials.
Multiplicity of zeros of polynomial functions
The real roots of a polynomial correspond to the x-intercepts of the graph of the polynomial. Therefore, we can find information about the number of real roots of a polynomial by looking at its graph.
Similarly, we can determine how many times the graph will touch or cross the x-axis by looking at the zeros of the polynomial or the factored form of the polynomial.
A zero or a root has a multiplicity, which refers to the number of times its associated factor appears in the polynomial. For example, the quadratic $latex (x+2)(x-3)$ has the roots $latex x=-2$ and $latex x=3$, each occurring only once.
The fifth-degree polynomial $latex {{(x+2)}^3}{{(x-3)}^2}$ has the same roots as the quadratic, but in this case, the root $latex x=-2$ has a multiplicity of 3 since the factor $latex (x+2)$ appears three times (it is cubed).
Similarly, the root $latex x = 3$ has a multiplicity of 2 since the factor $latex (x-3)$ appears twice (it is squared).
If we have a polynomial in its factored form, we can easily determine the multiplicity of the roots. We simply have to count the number of times each root appears in the polynomial.
If the polynomial is not in its factored form, we need to factor it if possible or obtain a graph of the polynomial to observe its behavior when crossing or touching the x-axis.
EXAMPLE
- Find the multiplicity of the roots of the polynomial $latex {{(x+5)}^2}{{(x-2)}^4}{{(x-3)}^3}$.
Solution: The roots of the polynomial are $latex x=-5$, $latex x=2$, and $latex x=3$. To find its multiplicity, we just have to count the number of times each root appears. In this case, the multiplicity is the exponent to which each factor is raised.
- The root $latex x=-5$ has a multiplicity of 2.
- The root $latex x=2$ has a multiplicity of 4.
- The root $latex x=3$ has a multiplicity of 3.
Multiplicity of roots of graphs of polynomials
Polynomial graphs behave differently at various x-intercepts. Sometimes the graph will completely cross the x-axis at an intercept. Other times, the graph will touch the x-axis and bounce.
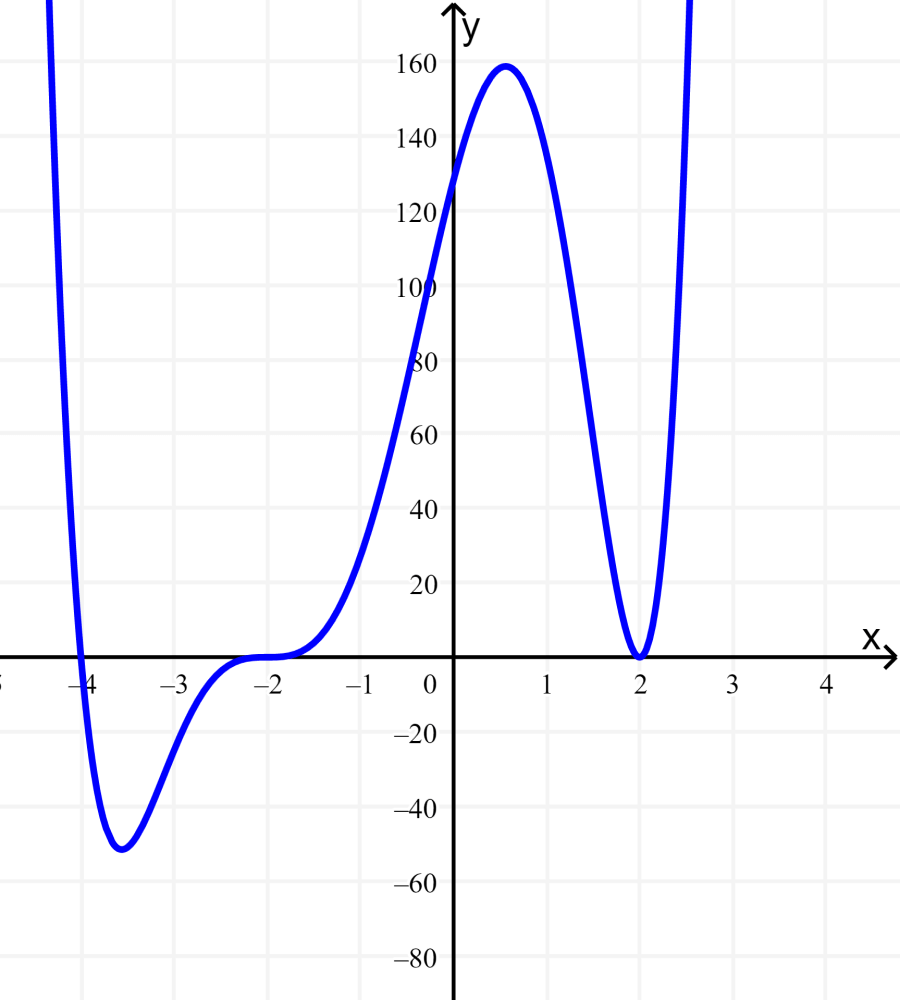
Suppose we have the graph of the polynomial function $latex f(x)=(x+4){{(x-2)}^2}{{(x+2)}^3}$. Notice that the behavior in each of the roots is different:
The intercept at $latex x=-4$ is the solution to the equation $latex x+4=0$. The graph passes directly through the intercept at $latex x=-4$. The factor is linear, so the behavior near the intercept is similar to a line. This is a single root since the root corresponds to a single factor.
The intercept at $latex x=2$ is the repeated solution of the equation $latex {{(x-2)}^2}=0$. The graph touches the x-axis at the intercept and changes direction.
The factor is quadratic, so the behavior near the intercept is similar to a quadratic, that is, it bounces when it hits the x-axis. The factor $latex (x-2)$ appears twice. Therefore, the root $latex x=2$ has multiplicity 2.
The intercept at $latex x=-2$ is the repeated solution of the factor $latex {{(x+2)}^3}=0$. The graph passes through the x-axis at the intercept but flattens out a bit as it crosses.
This factor is cubic, so the behavior near the intercept is cubic, that is, it has an S shape similar to the function $latex f(x)={{x}^3}$. This root has a multiplicity of 3.
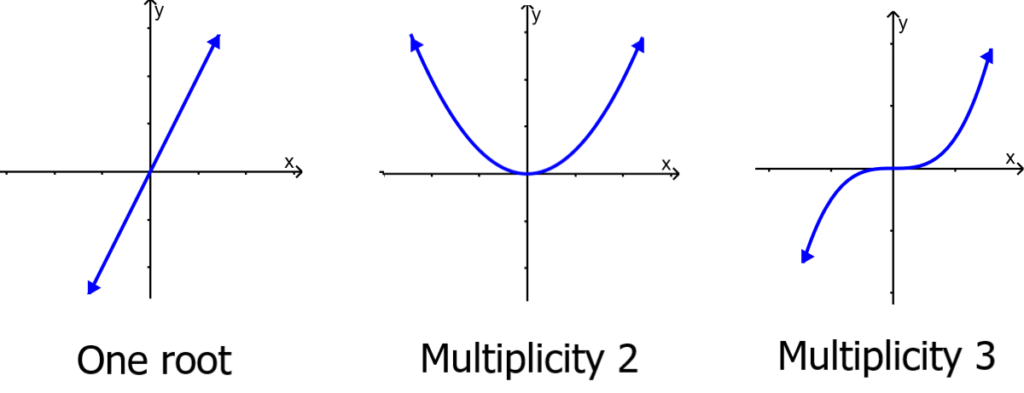
For roots with even multiplicities, the graphs touch or are tangent to the x-axis at these values of x. For roots with odd multiplicities, the graphs cross the x-axis at these x values. The following graphs illustrate the behavior of polynomials with multiplicities 1, 2, and 3.
For larger even powers like 4, 6, 8, the graph will keep touching the x-axis and bouncing, but with each increase in power, the graph will appear to flatten more and more as it gets closer and farther from the x-axis.
Likewise, for larger odd powers like 5, 7, 9, the graph will continue to cross the x-axis, but as the powers increase, the graph will appear to get flatter as you move closer to and farther from the x-axis.
Identify roots and their multiplicities using polynomial graphs
Therefore, summarizing what we have above, we can find the multiplicities of the roots of polynomials keeping the following in mind:
- If the graph crosses the x-axis and appears to be linear near the intercept, the root is unique.
- If the graph touches the x-axis and bounces, the root has an even multiplicity.
- If the graph crosses the x-axis at a root, then the root has odd multiplicity.
- The sum of the multiplicities is the degree n of the polynomial.
We are going to apply these ideas in the following example.
EXAMPLE
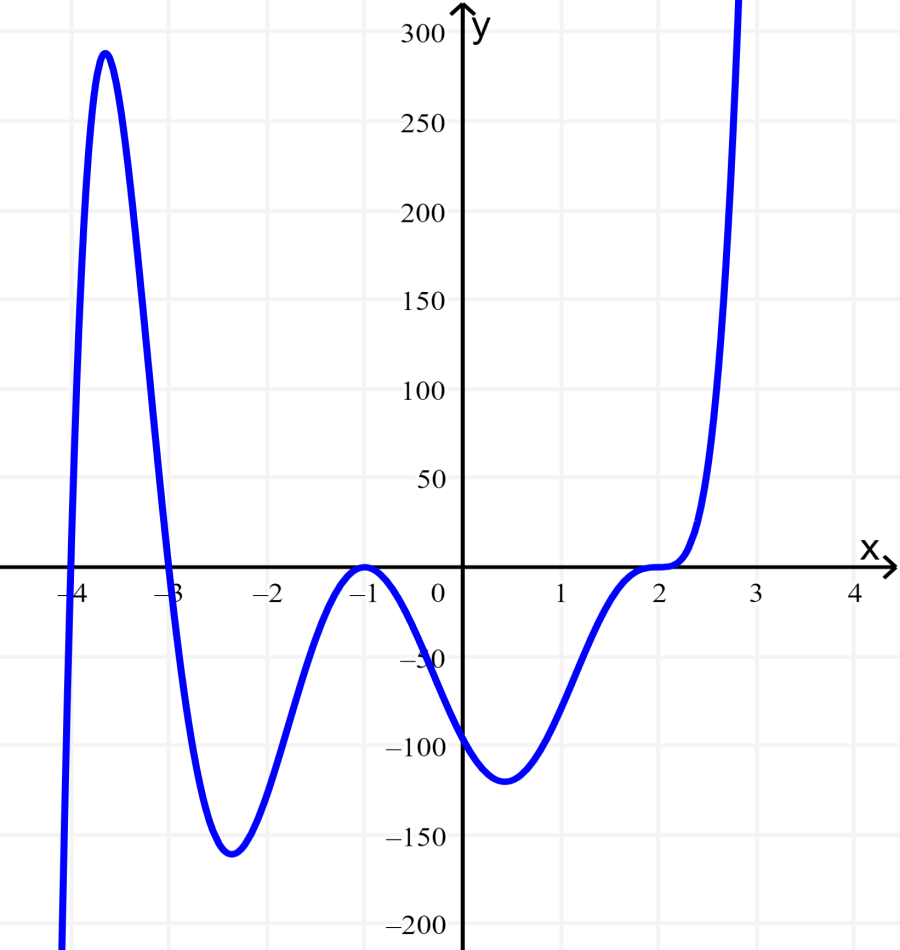
The graph below represents a polynomial of degree 7. Use this graph to find the roots of the polynomial and its possible multiplicities.
Solution: The polynomial function is of degree 7, so the sum of the multiplicities of the roots must equal 7.
Starting from the left, the first root occurs at $latex x=-4$. The graph looks almost linear at that point, so we know that this root has a multiplicity of 1.
Similarly, we see that the root that occurs at $latex x=-3$ also looks linear, so this root also has a multiplicity of 1.
Then we have a root at $latex x=-1$. We see that at this point, the graph touches the x-axis and bounces, so we know that the root must have even multiplicity. The root $latex x = -1$ has multiplicity 2.
The last zero occurs at $latex x = 2$. The graph crosses the x-axis, so the multiplicity of this root must be odd. We know that the multiplicity of this root must be 3 and the sum of the multiplicities is equal to 7.
See also
Interested in learning more about the complex roots of polynomials? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
