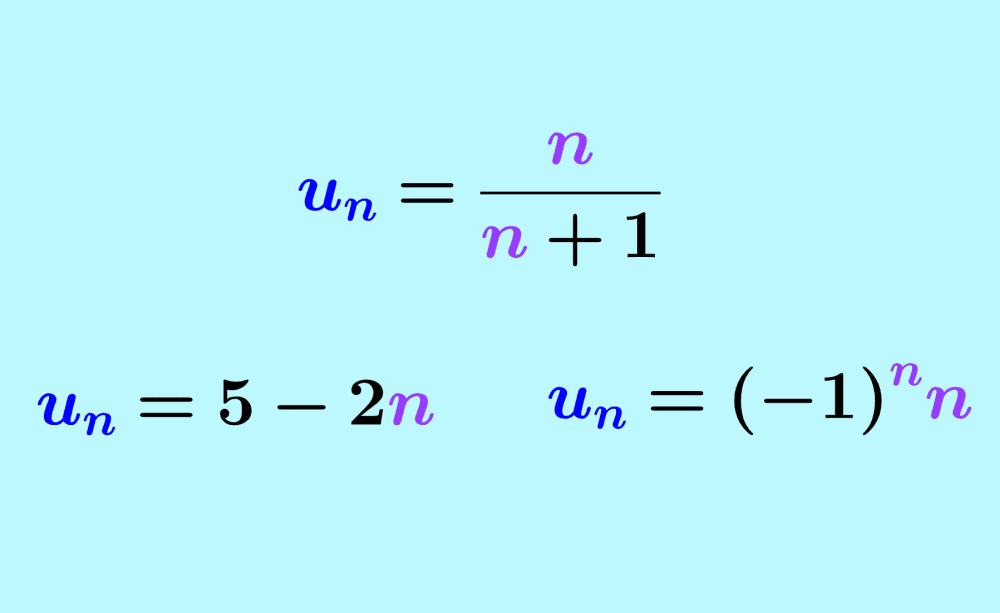Depending on the pattern of the numbers in the sequence, we can have several types of mathematical sequences. Among the most important, we have convergent and divergent sequences, oscillating sequences, and periodic sequences.
In this article, we will learn about the most important types of mathematical sequences. We will look at their definitions, important characteristics, and some examples.
Convergent sequences
Convergent sequences have the main characteristic of approaching a specific value as the number of terms in the sequence increases.
For example, consider the following sequence:
$$3,~2+\frac{1}{5},~2+\frac{1}{25},…,~2+\frac{1}{5^{n-1}},…$$
The terms of the sequence are getting closer and closer to the value of 2. This can be observed in a plot of $latex u_{n}$ (value of term n) vs $latex n$ (term number).
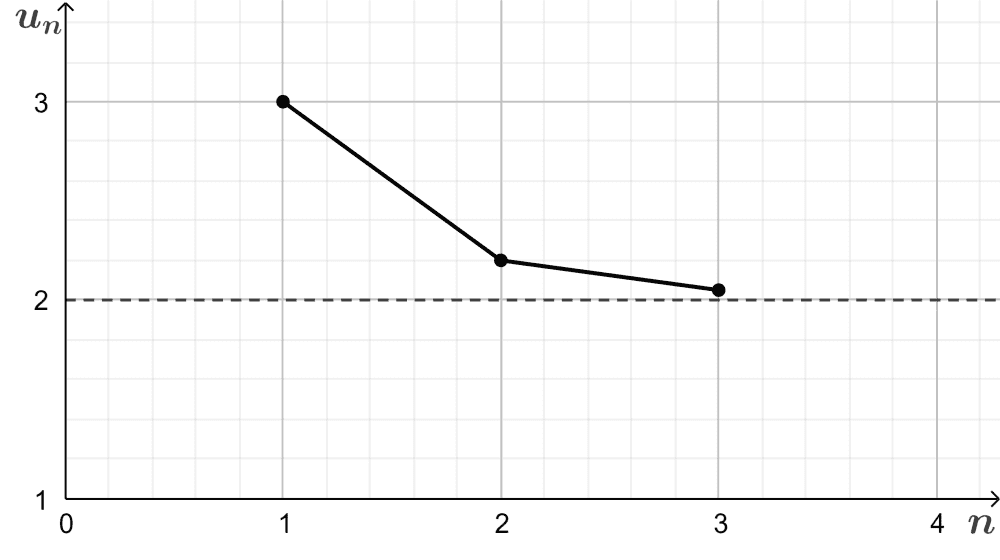
This is a convergent sequence since as the number of terms increases, the values of the terms tend to a definite limit. The value 2 is the limit of the sequence.
EXAMPLES
- The sequence $latex u_{n}=\frac{n}{n+1}$ is convergent. We can observe this by writing the first six terms of the sequence:
$$\frac{1}{2},~\frac{2}{3},~\frac{3}{4},~\frac{4}{5},~\frac{5}{6}, ~\frac{6}{7}$$
As the terms of the sequence increase, they get closer and closer to 1.
- The sequence $latex u_{n}=\frac{1}{n^2+1}$ is convergent. Writing the first six terms of the sequence, we have:
$$\frac{1}{2},~\frac{1}{5},~\frac{1}{10},~\frac{1}{17},~\frac{1}{26}, ~\frac{1}{37}$$
As the terms of the sequence increase, the value of each term becomes smaller and smaller and closer and closer to 0.
Divergent sequences
Divergent sequences are characterized by the fact that they move away from the initial value as the number of terms in the sequence increases.
For example, consider the following sequence:
$$5,~9,~13,~17,…,~4n+1$$
In this sequence, as the number of terms increases, the values of the terms increase and tend to infinity. We can observe this in the graph of $latex u_{n}$ vs $latex n$.
All sequences that don’t converge to a limit and move away from the initial value are considered divergent sequences.
EXAMPLES
- The sequence $latex u_{n}=5-2n$ is divergent. Writing the first six terms of the sequence, we have:
$$3,~1,~-1,~-3,~-5, ~-7$$
As the terms of the sequence increase, the values move toward negative infinity and away from the initial value.
- The sequence $latex u_{n}=(-1)^nn$ is divergent. Writing the first six terms of the sequence, we have:
$$-1,~2,~-3,~4,~-5, ~6$$
The terms of the sequence oscillate between negative and positive, but each time they move away from the initial value and become larger (positive and negative).
Oscillating sequences
Oscillating sequences are sequences in which the values of the terms oscillate with respect to a specific value. Oscillating sequences can be convergent or divergent.
For example, consider the following sequence:
$$1+\frac{1}{2},~1-\frac{1}{4},~1+\frac{1}{8},…, 1+(-1)^{n-1}\left(\frac{1}{2}\right)^n,…$$
As the number of terms increases, the sequence oscillates with respect to the value of 1, but at the same time it is getting closer and closer to 1:
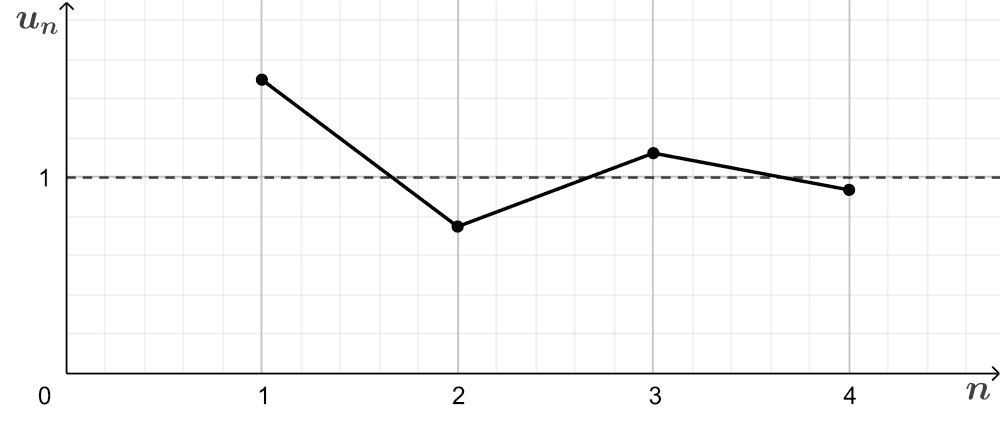
In this case, the sequence is oscillating and convergent, since it is converging to the limit of 1.
Similarly, a sequence can oscillate and diverge at the same time. For example, consider the following sequence:
$$ -2.5,~5, ~-10,~20,~-40,…,~5(-2)^{n-1}, …$$
In this case, we can observe that the sequence is oscillatory and is not converging to any particular value. That is, the sequence is divergent.
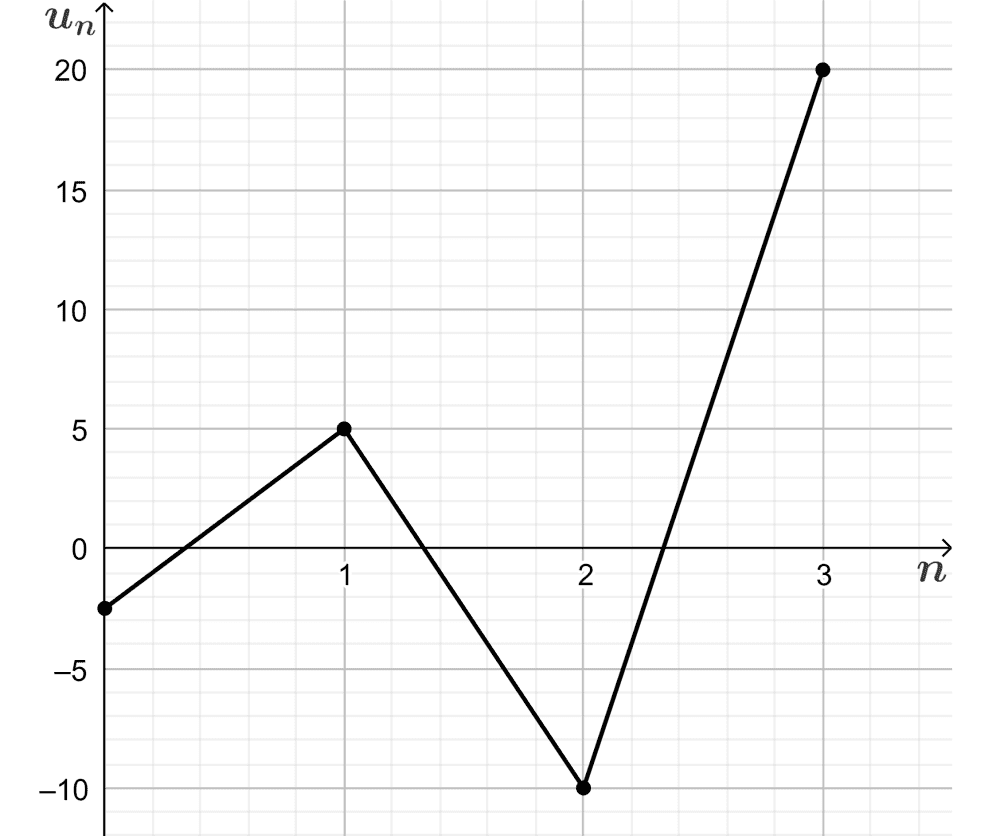
EXAMPLES
- The sequence $latex u_{n+1}=8-3u_{n}$, where $latex u_{n}$ is oscillating. Writing the first six terms of the sequence, we have:
$$3,~-1,~11,~-25,~83, ~-241$$
We see that the terms oscillate between positive and negative. In addition, the values become larger and larger, so the sequence is also divergent.
- The sequence $latex u_{n}=\frac{(-1){n+1}}{n^2}$ is oscillating. Writing the first six terms of the sequence, we have:
$$1,~-\frac{1}{4},~\frac{1}{9},~-\frac{1}{16},~\frac{1}{25},~-\frac{1}{36}$$
In this sequence, the terms also range from negative to positive. In addition, the sequence is also convergent.
Periodic sequences
Periodic sequences are characterized by the fact that the values of their terms repeat after a certain interval.
For example, consider the following sequence:
$$ 1, ~3,~1, ~3, …, 2+(-1)^n,…$$
As the number of terms increases, the sequence simply contains the terms 1 and 3. In this case, the period is 2.
EXAMPLES
- The sequence $latex u_{n+1}=3-u_{n}$, where $latex u_{1}=2$ is periodic. The first six terms of the sequence are:
$$2,~1,~2,~1,~2,~1$$
We can see that the values repeat between 2 and 1.
- The sequence $latex u_{n+1}=\frac{1}{u_{n}}$, where $latex u_{1}=7$ is periodic. Writing the first six terms of the sequence, we have:
$$7,~\frac{1}{7},~7,~\frac{1}{7},~7, ~\frac{1}{7}$$
We can see that the values repeat between 7 and $latex \frac{1}{7}$.
See also
Interested in learning more about sequences? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
