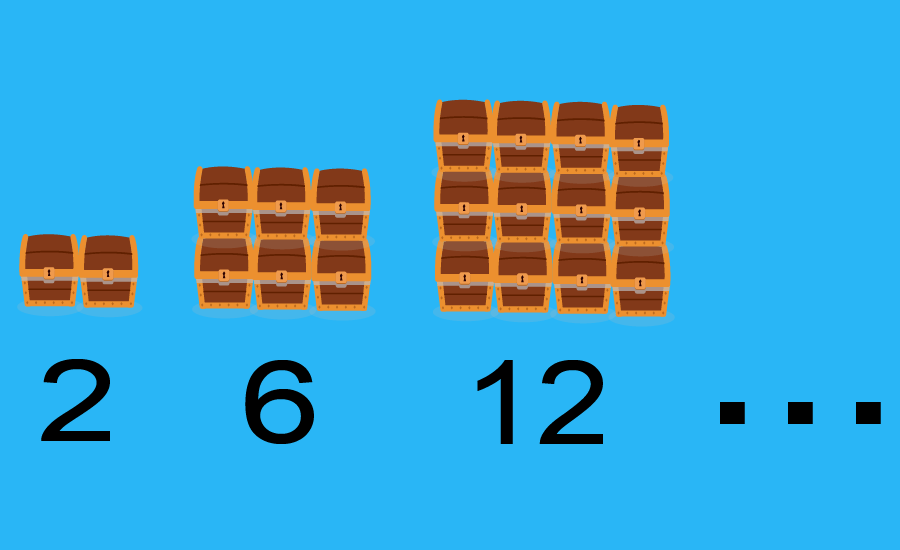The two most straightforward sequences we can work with are arithmetic and geometric sequences. Arithmetic sequences are characterized in that their terms are formed by adding a common difference. On the other hand, geometric sequences are formed by multiplying the terms by a common ratio.
In this article, we will explore these sequences and learn how to write terms for both arithmetic and geometric sequences. We will also learn how to solve some practice problems.
Arithmetic sequences
An arithmetic sequence is a list of numbers with a defined pattern. If we take a number from the sequence and then subtract it by the previous number and the result is always the same, then it is an arithmetic sequence.
The constant difference in all pairs of consecutive numbers in a sequence is called the common difference, denoted by the letter d. We use the common difference to go from one term to another.
If we take a term in the sequence and add the common difference, we will move to the next term. This is how the terms in an arithmetic sequence are generated.
If the common difference between the terms is positive, we say that the sequence is increasing. On the other hand, when the difference between the terms is negative, we say that the sequence is decreasing.
The following are two examples of arithmetic sequences. Look at their common differences.
Formula of the arithmetic sequence
If we want to find any term (as the n term) in the arithmetic sequence, we can use the arithmetic sequence formula to accomplish this. All we have to do is extract or identify values from the problem that will be substituted in the formula.
Let’s see the essential parts of the formula:
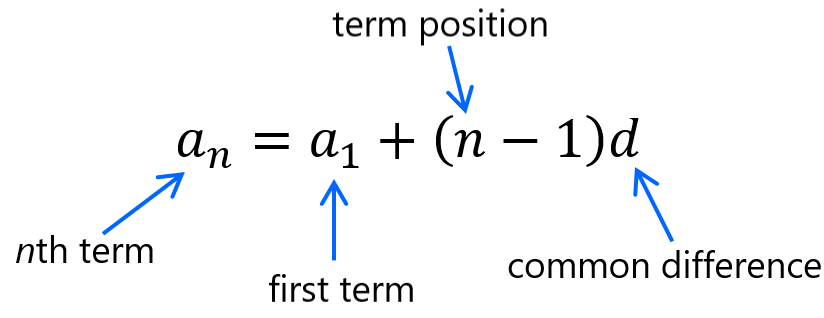
where we have:
- $latex {{a}_{n}}=$ term we want to find
- $latex {{a}_{1}}=$ first term in the ordered list of numbers
- $latex n=$ the position of the term, for example, 5 for the fifth term
- $latex d=$ the common difference of any pair of consecutive terms
Examples of arithmetic sequences
EXAMPLE 1
Find the next term in the following sequence:
4, 7, 10, 13, 16, ?
Solution
First, we find the common difference in each pair of consecutive numbers:
- $latex 7-4=3$
- $latex 10-7=3$
- $latex 13-10=3$
- $latex 16-13=3$
Given that $latex d=3$, we can find the term that follows after 16 simply by adding 3. So, we have $latex 16+3=19$.
4, 7, 10, 13, 16, 19
EXAMPLE 2
Find the next term in the following sequence:
29, 22, 15, 8, ?
Solution
First, we find the common difference in each pair of consecutive numbers:
- $latex 22-29=-7$
- $latex 15-22=-7$
- $latex 8-15=-7$
Given that $latex d=-7$, we can find the term that follows the 8 by simply adding -7. So, we have $latex 8+(-7)=1$.
29, 22, 15, 8, 1
EXAMPLE 3
Find the 20th term in the following arithmetic sequence:
3, 6, 9, 12, …
Solution
We need three things to find the term 20 using the formula:
- The first term $latex ({{a}_{1}})$
- The common difference between consecutive terms $latex (d)$
- The position of the term $latex (n)$
Then, we have:
- first term $latex ={{a}_{1}}=3$
- common difference $latex =d=3$
- term position $latex =n=20$
and we substitute the values in the formula:
$latex {{a}_{n}}={{a}_{1}}+(n-1)d$
$latex {{a}_{20}}=3+(20-1)3$
$latex {{a}_{20}}=3+(19)3$
$latex {{a}_{20}}=3+57$
$latex {{a}_{20}}=60$
EXAMPLE 4
Find the 15th term in the following arithmetic sequence:
25, 21, 17, 13, …
Solution
We need three things to find 15th term using the formula:
- The first term $latex ({{a}_{1}})$
- The common difference between consecutive terms $latex (d)$
- The position of the term $latex (n)$
Then, we have:
- first term $latex ={{a}_{1}}=25$
- common difference $latex =d=-4$
- term position $latex =n=15$
and we substitute the values in the formula:
$latex {{a}_{n}}={{a}_{1}}+(n-1)d$
$latex {{a}_{15}}=25+(15-1)(-4)$
$latex {{a}_{15}}=25+(14)(-4)$
$latex {{a}_{15}}=25-56$
$latex {{a}_{15}}=-31$
EXAMPLE 5
Find the 22nd term in the following arithmetic sequence:
5, 11, 17, 23, …
Solution
We need three things to find the 22nd term using the formula:
- The first term $latex ({{a}_{1}})$
- The common difference between consecutive terms $latex (d)$
- The position of the term $latex (n)$
Then, we have:
- first term $latex ={{a}_{1}}=5$
- common difference $latex =d=6$
- term position $latex =n=22$
and we substitute the values in the formula:
$latex {{a}_{n}}={{a}_{1}}+(n-1)d$
$latex {{a}_{22}}=5+(22-1)6$
$latex {{a}_{22}}=5+(21)6$
$latex {{a}_{22}}=5+126$
$latex {{a}_{22}}=131$
Try solving the following practice problems
Geometric sequences
A geometric sequence is a sequence of numbers that follows a pattern where the next term is found by multiplying by a constant called the common ratio, r.
Similar to arithmetic sequences, geometric sequences can also increase or decrease. However, in geometric sequences, this depends on whether the common ratio is greater than 1 or less than 1:
Formula of geometric sequences
If we want to find any term (like the n term) in the geometric sequence, we can use the geometric sequence formula to accomplish this. We only need to extract the necessary information from the problem to replace in the formula.
The following are the essential parts of the formula:
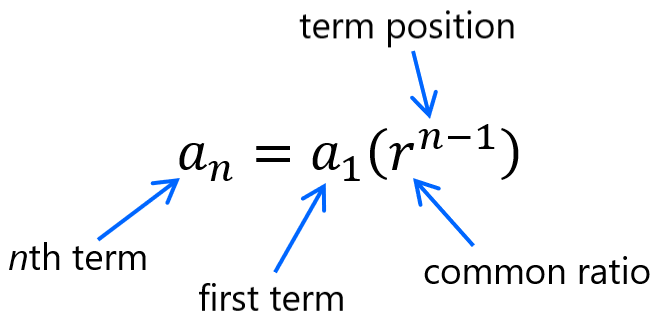
where, we have:
- $latex {{a}_{n}}=$ term we want to find
- $latex {{a}_{1}}=$ first term in the sequence
- $latex n=$ position of the term, for example, 4 for the fourth term
- $latex r=$ common ratio
The common ratio can be calculated by dividing a term by the previous term:
$$r=\frac{{{{a}_{n}}}}{{{{a}_{{n-1}}}}}$$
Examples of geometric sequences
EXAMPLE 1
Find the next term in the following sequence:
5, 15, 45, 135, ?
Solution
First, we find the common ratio in each pair of consecutive numbers:
- $latex r=\frac{15}{5}=3$
- $latex r=\frac{45}{15}=3$
- $latex r=\frac{135}{45}=3$
Given that $latex r=3$, we can find the term that follows after 135 simply by multiplying by 3. So, we have $latex 135(3)=405$.
5, 15, 45, 135, 405
EXAMPLE 2
Find the next term in the following sequence:
4, -20, 100, -500, 2500, ?
Solution
First, we find the common ratio in each pair of consecutive numbers:
- $latex r=\frac{-20}{4}=-5$
- $latex r=\frac{100}{-20}=-5$
- $latex r=\frac{-500}{100}=-5$
- $latex r=\frac{2500}{-500}=-5$
Given that $latex r=-5$, we can find the term that follows after 2500 simply by multiplying by -5. Therefore, we have $latex 2500(-5)=-12500$.
4, -20, 100, -500, 2500, -12500
EXAMPLE 3
Find the next term in the following sequence:
-80, 40, -20, 10 ?
Solution
First, we find the common ratio in each pair of consecutive numbers:
- $latex r=\frac{40}{-80}=-0.5$
- $latex r=\frac{-20}{40}=-0.5$
- $latex r=\frac{10}{-20}=-0.5$
Given that $latex r=-0.5$, we can find the term that follows the 10 simply by multiplying by -0.5. Therefore, we have $latex 10(-0.5)=-5$.
-80, 40, -20, 10, -5
EXAMPLE 4
Find the 10th term in the following geometric sequence:
2, 4, 8, 16, …
Solution
We need three things to find the 10th term using the formula:
- The first term $latex ({{a}_{1}})$
- The common ratio between consecutive terms $latex (r)$
- The position of the term $latex (n)$
Then, we have:
- first term $latex ={{a}_{1}}=2$
- common ratio $latex =r=\frac{4}{2}=2$
- term position $latex =n=10$
and we substitute the values in the formula:
$latex {{a}_{n}}={{a}_{1}}\left( {{{r}^{{n-1}}}} \right)$
$latex {{a}_{10}}=2\left( {{{2}^{{10-1}}}} \right)$
$latex {{a}_{10}}=2\left( {{{2}^{{9}}}} \right)$
$latex {{a}_{10}}=2(512)$
$latex {{a}_{10}}=1024$
EXAMPLE 5
Find the 6th term in the following geometric sequence:
3, 12, 48, 192, …
Solution
We need three things to find term 6 using the formula:
- The first term $latex ({{a}_{1}})$
- The common ratio between consecutive terms $latex (r)$
- The position of the term $latex (n)$
Therefore, we have:
- first term $latex ={{a}_{1}}=3$
- common ratio $latex =r=\frac{12}{3}=4$
- position term $latex =n=6$
and we substitute the values in the formula:
$latex {{a}_{n}}={{a}_{1}}\left( {{{r}^{{n-1}}}} \right)$
$latex {{a}_{6}}=3\left( {{{4}^{{6-1}}}} \right)$
$latex {{a}_{6}}=3\left( {{{4}^{{5}}}} \right)$
$latex {{a}_{6}}=3(1024)$
$latex {{a}_{6}}=3072$
EXAMPLE 6
Find the 6th term in the following geometric sequence:
-2400, 1200, -600, 300, …
Solution
We need three things to find the 6th term using the formula:
- The first term $latex ({{a}_{1}})$
- The common ratio between consecutive terms $latex (r)$
- The position of the term $latex (n)$
Then, we have:
- first term $latex ={{a}_{1}}=-2400$
- common ratio $latex =r=\frac{1200}{-2400}=-0.5$
- term position $latex =n=6$
and we substitute the values in the formula:
$latex {{a}_{n}}={{a}_{1}}\left( {{{r}^{{n-1}}}} \right)$
$latex {{a}_{6}}=-2400\left( {{{-0.5}^{{6-1}}}} \right)$
$latex {{a}_{6}}=-2400\left( {{{-0.5}^{{5}}}} \right)$
$latex {{a}_{6}}=-2400(-0.03125)$
$latex {{a}_{6}}=75$
Try solving the following practice problems
See also
Interested in learning more about sequences? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
