The sum to infinity of a geometric sequence can be calculated when the common ratio is a number less than 1 and greater than -1. For this, we simply need the value of the first term and the value of the common ratio. We then use these values in a standard formula.
Here, we will explore the formula that we can use to find the sum to infinity of a geometric sequence. Then, we will apply this formula to solve some exercises.
Formula for the sum to infinity of geometric sequence
The sum to infinity of a geometric sequence can be calculated when we have $latex -1<r<1$. For example, consider the following sequence:
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…\left(\frac{1}{2}\right)^n$$
We can see that as the number of terms increases, the value of each term gets smaller and smaller.
That is, as $latex n \rightarrow \infty$, the term $latex \left(\frac{1}{2}\right)^n\rightarrow 0$, therefore the sum to infinity of the sequence has a specific value.
To find the sum to infinity of a geometric sequence, we use the following formula:
$$S_{\infty}= \frac{a}{1-r}$$
where $latex -1<r<1$. If the common ratio doesn’t meet this condition, the infinite sum does not exist.
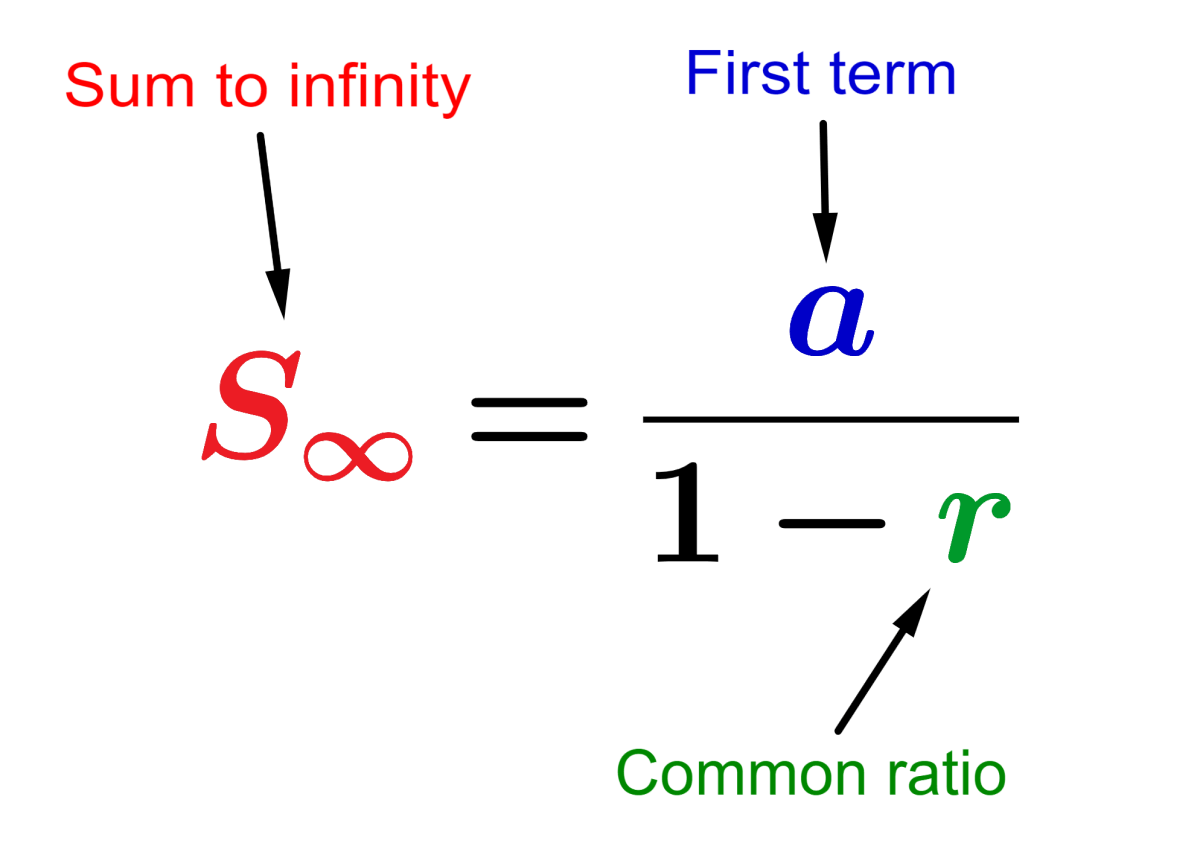
Proof of the formula for the sum to infinity of geometric sequences
Recall that we can find the sum of the first $latex n$ terms of any geometric sequence using the following formula:
$$S_{n}=\frac{a(1-r^n)}{1-r}$$
If the common ratio satisfies the condition $latex -1<r<1$, as $latex n\rightarrow \infty$, we have $latex r^n\rightarrow 0$.
Basically, this means that the $latex r^n$ term of the progression gets smaller and smaller until its value gets closer and closer to 0.
Therefore, as $latex n\rightarrow \infty$, we have:
$$S_{n}\rightarrow \frac{a(1-0)}{1-r}=\frac{a}{1-r}$$
Therefore, we prove that the sum to infinity of a geometric sequence where $latex -1<r<1$ is given by:
$$S_{\infty}=\frac{a}{1-r}$$
We note that the proof begins by assuming that $latex -1<r<1$. If this is not the case, the sum to infinity does not exist.
Examples of the sum to infinity of geometric sequences
EXAMPLE 1
Find the sum to infinity of the following geometric sequence:
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…$$
Solution
We start by writing the information we know:
- First term: $latex a=1$
- Common ratio: $latex r=\frac{1}{2}$
Now, we use the formula for the sum to infinity of a geometric sequence:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{1}{1-\frac{1}{2}}$$
$$=\frac{1}{\frac{1}{2}}$$
$latex S_{\infty}=2$
EXAMPLE 2
Find the sum to infinity of a geometric sequence in which the first term is equal to -3 and the common ratio is equal to $latex -\frac{1}{2}$.
Solution
In this case, we have the following values:
- First term: $latex a=-3$
- Common ratio: $latex r=-\frac{1}{2}$
By applying the formula for the sum to infinity of a geometric sequence, we have:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{-3}{1+\frac{1}{2}}$$
$$=\frac{-3}{\frac{3}{2}}$$
$latex S_{\infty}=-2$
EXAMPLE 3
Find the sum to infinity of the following geometric sequence:
$$2+\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+…$$
Solution
In this case, we have the following
- First term: $latex a=2$
- Common ratio: $latex r=\frac{1}{4}$
When we use the formula for the sum to infinity, we have:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{2}{1-\frac{1}{4}}$$
$$=\frac{2}{\frac{3}{4}}$$
$$S_{\infty}=\frac{8}{3}$$
EXAMPLE 4
Find the result of the following sum:
$$\sum_{r=1}^{\infty}\left(\frac{1}{5}\right)^r$$
Solution
Here, we have the sum of the geometric sequence written in sigma notation. We find the value of the first term by using $latex r=1$.
The common ratio is the number inside the parentheses, so we have:
- First term: $latex a=\frac{1}{5}$
- Common ratio: $latex r=\frac{1}{5}$
Using the formula for the sum to infinity with these values, we have:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{1}{5}}{1-\frac{1}{5}}$$
$$=\frac{\frac{1}{5}}{\frac{4}{5}}$$
$$=\frac{5}{20}$$
$$S_{\infty}=\frac{1}{4}$$
EXAMPLE 5
Write the recurring decimal 0.3232… as the sum of a geometric sequence, and then write the decimal as a rational number.
Solution
To solve this exercise, we begin by writing the decimal as the sum of a geometric sequence:
$$0.323232…= \frac{32}{100}+\frac{32}{10000}+\frac{32}{1000000}+…$$
Now, we identify the following values:
- $latex a=\frac{32}{100}$
- $latex r=\frac{1}{100}$
Since $latex -1<r<1$, we can calculate the value of the sum to infinity:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{32}{100}}{1-\frac{1}{100}}$$
$$=\frac{\frac{32}{100}}{\frac{99}{100}}$$
$$S_{\infty}=\frac{32}{99}$$
Therefore, the recurring decimal 0.3232…, can be written as $latex \frac{32}{99}$.
EXAMPLE 6
Express the recurring decimal 0.7272… as a fraction in its simplest form.
Solution
We write to the decimal as a geometric sequence:
$$0.727272…= \frac{72}{100}+\frac{72}{10000}+\frac{72}{1000000}+…$$
Now, we can see that the sequence has the following values:
- $latex a=\frac{72}{100}$
- $latex r=\frac{1}{100}$
Since $latex -1<r<1$, we can calculate the value of the sum to infinity:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{72}{100}}{1-\frac{1}{100}}$$
$$=\frac{\frac{72}{100}}{\frac{99}{100}}$$
$$=\frac{72}{99}$$
$$S_{\infty}=\frac{8}{11}$$
Therefore, the recurring decimal 0.7272…, can be written as $latex \frac{8}{11}$.
Sum to infinity of geometric sequences – Practice problems
Find the sum to infinity of the following geometric sequence $$4+\frac{4}{3}+\frac{4}{9}+…$$
Write the answer in the input box.
See also
Interested in learning more about geometric sequences? You can ake a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
