We can find the first term of a geometric sequence using the formula for the nth term. We then plug in the values of the common ratio and of any term in the sequence, along with its position, and solve for a.
Here, we will learn how to find the first term of geometric sequences. We will look at its formula and apply it to solve some practice exercises.
Steps to find the first term of a geometric sequence
A geometric sequence has the main characteristic that each term is formed by multiplying the previous term by a specific value. This value is called the common ratio.
For example, the sequence 2, 6, 18, 54, …, is formed by multiplying each term by 3 to obtain the next term. That is, the common ratio is 3.
Recall that the formula for finding any term in a geometric sequence is
$$a_{n}=ar^{n-1}$$
where,
- $latex a$ is the first term of the sequence.
- $latex r$ is the common ratio.
- $latex n $ is the position of the term.
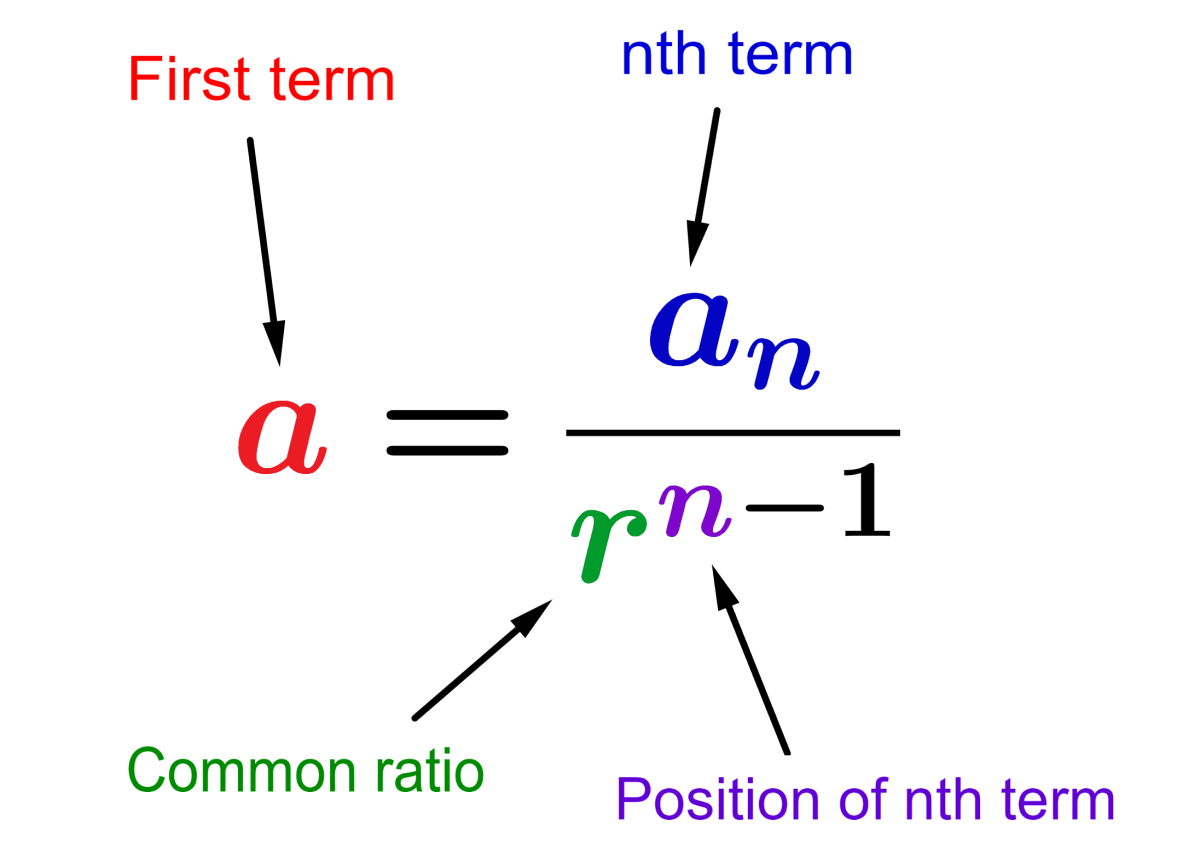
Therefore, we can rewrite this formula as follows to find the first term:
$$a=\frac{a_{n}}{r^{n-1}}$$
Then, we can find the first term of a geometric sequence with these steps:
1. Find the common ratio.
We can find the common ratio by dividing any term by its previous term.
2. Identify the value of any term in the sequence and its position.
The position of the term is the value of $latex n$.
3. Use the formula for the first term.
Use the values from steps 1 and 2 into the formula $latex a=\frac{a_{n}}{r^{n-1}}$.
Solved examples of the first term of geometric sequences
EXAMPLE 1
Find the value of the first term of a geometric sequence where the 4th term is equal to 24 and the common ratio is 2.
Solution
The statement gives us the values of the 4th term and the common ratio, so we can identify the following information:
- $latex a_{n}=a_{4}=24$
- $latex n=4$
- $latex r=2$
Now, we use these values into the formula for the first term of a geometric sequence:
$$a=\frac{a_{n}}{r^{n-1}}$$
$$a=\frac{24}{2^{4-1}}$$
$$a=\frac{24}{2^3}$$
$$a=\frac{24}{8}$$
$latex a=3$
EXAMPLE 2
What is the first term of a geometric sequence in which the 5th term is equal to 81 and the common ratio is equal to 3?
Solution
Here, we also know the values of a term and the common ratio. Then, we have the following:
- $latex a_{n}=a_{5}=81$
- $latex n=5$
- $latex r=3$
Using the formula for the first term of a geometric sequence, we have:
$$a=\frac{a_{n}}{r^{n-1}}$$
$$a=\frac{81}{3^{5-1}}$$
$$a=\frac{81}{3^4}$$
$$a=\frac{81}{81}$$
$latex a=1$
EXAMPLE 3
Find the first term of a geometric sequence where the 6th term is equal to 128 and the common ratio is -2.
Solution
We know the values of the 6th term and the common ratio. Then, we have the following:
- $latex a_{n}=a_{6}=128$
- $latex n=6$
- $latex r=-2$
When we use these values into the formula for the first term, we have:
$$a=\frac{a_{n}}{r^{n-1}}$$
$$a=\frac{128}{-2^{6-1}}$$
$$a=\frac{128}{-2^5}$$
$$a=\frac{128}{-32}$$
$latex a=-4$
EXAMPLE 4
In a geometric sequence we have $latex a_{4}=32$ and $latex a_{5}=64$. What is the value of the first term?
Solution
In this case, we don’t know the common ratio directly, but we have the following information:
- $latex a_{4}=32$
- $latex a_{5}=64$
Therefore, we can find the value of the common ratio by dividing the value of the 5th term by the value of the 4th term:
$$r=\frac{a_{5}}{a_{4}}$$
$$r=\frac{64}{32}=2$$
Now, we use the common ratio to find the first term (we can use any $latex a_{4}$ or $latex a_{5}$ term):
$$a=\frac{a_{n}}{r^{n-1}}$$
$$a=\frac{32}{2^{4-1}}$$
$$a=\frac{32}{2^3}$$
$$a=\frac{32}{8}$$
$latex a=4$
EXAMPLE 5
Find the value of the first term of a geometric sequence where we have $latex a_{6}=30$ and $latex a_{7}=15$.
Solution
Similar to the previous example, we start with the following information:
- $latex a_{6}=30$
- $latex a_{7}=15$
Then, we use these values to find the value of the common ratio:
$$r=\frac{a_{7}}{a_{6}}$$
$$r=\frac{15}{30}=\frac{1}{2}$$
Now, we use these values to find the first term:
$$a=\frac{a_{n}}{r^{n-1}}$$
$$a=\frac{30}{(\frac{1}{2})^{6-1}}$$
$$a=\frac{30}{(\frac{1}{2})^5}$$
$$a=\frac{30}{\frac{1}{32}}$$
$latex a=960$
EXAMPLE 6
If we have $latex a_{4}=48$ and $latex a_{6}=12$, find the possible values of the first term of the geometric sequence.
Solution
We have the following information:
- $latex a_{4}=48$
- $latex a_{6}=12$
The common ratio is equal to $latex r=\frac{a_{6}}{a_{5}}$ and also $latex r=\frac{a_{5}}{a_{4}}$.
Therefore, we can solve one of the equations for $latex a_{5}$ and substitute into the second equation. In the second equation, $latex a_{5}=ra_{4}$. Then:
$$r=\frac{a_{6}}{a_{5}}$$
$$r=\frac{a_{6}}{ra_{4}}$$
$$r=\frac{12}{48r}$$
$latex 48r^2=12$
$$r^2=\frac{1}{4}$$
$latex r=\pm \frac{1}{2}$
Now, we use the formula of the first term:
$$a=\frac{a_{n}}{r^{n-1}}$$
$$a=\frac{48}{(\frac{1}{2})^{4-1}}$$
$$a=\frac{48}{(\pm \frac{1}{2})^3}$$
$$a=\frac{48}{\pm \frac{1}{8}}$$
$latex a=\pm 384$
First term of geometric sequences – Practice problems
Find the first term of a geometric sequence where the second term is equal to -12 and the fifth term is equal to 768.
Write the answer in the input box.
See also
Interested in learning more about geometric sequences? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
