A system of equations consists of two or more equations with two or more variables, all of which share the same solution. One of the methods used to solve systems of two equations with two variables is the elimination method. This method consists of multiplying one of the equations by a number, so that by adding the equations, we eliminate one of the variables.
Here, we will learn how to solve systems of equations using the method of elimination. Then we will solve several practice problems using this method.
ALGEBRA
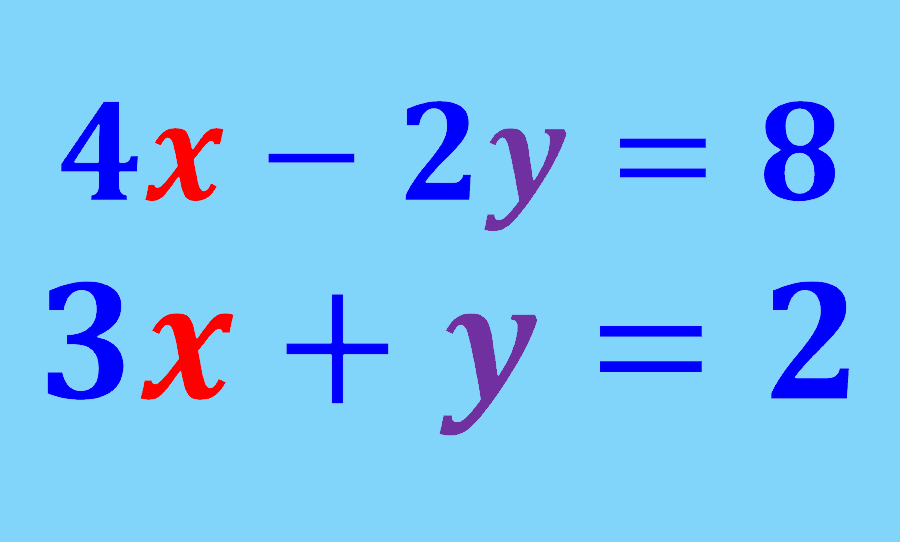
Relevant for…
Learning to solve systems of equations with the elimination method.
ALGEBRA
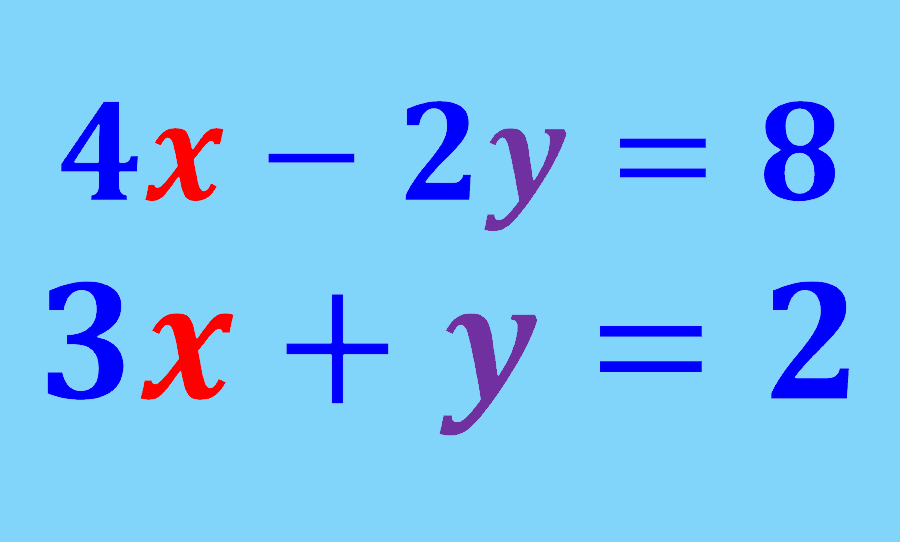
Relevant for…
Learning to solve systems of equations with the elimination method.
Steps to solve systems of equations by elimination
The elimination method to solve systems of equations consists of multiplying one of the equations by a number, so that when adding both equations, one of the variables is eliminated.
In detail, we can follow the following steps to solve systems of equations by elimination:
1. Simplify both equations.
This includes removing parentheses, eliminating fractions, and combining like terms.
2. Write the equations in the form Ax+By=C.
3. Manipulate the equations to obtain opposite coefficients in one of the variables.
We have to eliminate one of the variables when adding the equations. Therefore, we have to make one coefficient a and the other –a in one of the variables.
For example, if we have 2x in one equation and 3x in the other, we multiply the first by 3 and the second by -2 to get 6 and -6 respectively.
4. Add the equations.
By doing this, we will obtain a single equation with a single variable.
5. Solve the equation from step 4 for the remaining variable.
If you need to review, you can take a look at our article on how to solve linear equations with one variable.
6. Find the value of the second variable.
Substitute the value from step 5 into either of the two equations and solve for the second variable.
Systems of equations by elimination – Examples with answers
EXAMPLE 1
Use the elimination method to solve the system: $latex \begin{cases}x-y=3 \\ 2x+y=12 \end{cases}$
Solution
Steps 1 and 2: The equations are already simplified and are already in the form Ax+By=C.
Step 3: We have opposite coefficients in the variable y.
Step 4: Adding the equations, we have:
$latex x-y=3$
$latex + \hspace{1cm} 2x+y=12$
___________________
$latex 3x=15$
Step 5: Solving for x, we have:
$latex 3x=15$
$latex x=5$
Step 6: Substituting $latex x=5$ into the second equation, we have:
$latex 2x+y=12$
$latex 2(5)+y=12$
$latex 10+y=12$
$latex y=2$
The solution to the system of equations is $latex x=5,~~y=2$.
EXAMPLE 2
Find the solution to the system of equations using the elimination method: $latex \begin{cases}y=2x+7 \\ -6x-2y=-4 \end{cases}$
Solution
Step 1: We can divide the second equation by -2:
$latex \begin{cases}y=2x+7 \\ 3x+y=2 \end{cases}$
Step 2: We write the equations in the form Ax+By=C:
$latex \begin{cases}-2x+y=7 \\ 3x+y=2 \end{cases}$
Step 3: We multiply the first equation by -1 to get opposite coefficients in y:
$latex \begin{cases}2x-y=-7\\ 3x+y=2 \end{cases}$
Step 4: Adding the equations, we have:
$latex 2x-y=-7$
$latex + \hspace{1cm} 3x+y=2$
___________________
$latex 5x=-5$
Step 5: We solve for x:
$latex 5x=-5$
$latex x=-1$
Step 6: Substituting $latex x=-1$ into the first equation, we have:
$latex y=2x+7$
$latex y=2(-1)+7$
$latex y=5$
The solution is $latex x=-1, ~~y=5$.
EXAMPLE 3
Solve the system of equations: $latex \begin{cases}2x=3y-14 \\ 2y=x+8 \end{cases}$
Solution
Step 1: The equations are already simplified.
Step 2: Writing the equations in the form Ax+By=C, we have:
$latex \begin{cases}2x-3y=-14 \\ -x+2y=8 \end{cases}$
Step 3: We multiply the second equation by 2 to obtain opposite coefficients in x:
$latex \begin{cases}2x-3y=-14 \\ -2x+4y=16 \end{cases}$
Step 4: Adding the equations, we have:
$latex 2x-3y=-14$
$latex + \hspace{1cm} -2x+4y=16$
___________________
$latex y=2$
Step 5: We already got the value of y:
$latex y=2$
Step 6: Using the value $latex y=2$ in the first equation, we have:
$latex 2x=3y-14$
$latex 2x=3(2)-14$
$latex 2x=-8$
$latex x=-4$
The solution is $latex x=-4,~~y=2$.
EXAMPLE 4
Solve the system of equations: $latex \begin{cases}2x-3y=7 \\ 2x+3y=1 \end{cases}$
Solution
Steps 1 and 2: We have nothing to simplify, and the equations are already in the form Ax+By=C.
Step 3: We already have opposite coefficients in y.
Step 4: Adding the equations, we have:
$latex 2x-3y=7$
$latex + \hspace{1cm} 2x+3y=1$
___________________
$latex 4x=8$
Step 5: Solving the equation, we have:
$latex x=2$
Step 6: Using the value $latex x=2$ in the second equation, we have:
$latex 2x+3y=1$
$latex 2(2)+3y=1$
$latex 4+3y=1$
$latex 3y=-3$
$latex y=-1$
The solution is $latex x=2,~~y=-1$.
EXAMPLE 5
Find the solution to the system of equations: $latex \begin{cases}3x-y=1 \\ 5x+y=7 \end{cases}$
Solution
Steps 1 and 2: The equations are now simplified and written in the form Ax+By=C.
Step 3: We already have opposite coefficients in y:
$latex \begin{cases}3x-y=1 \\ 5x+y=7 \end{cases}$
Step 4: Adding the equations, we have:
$latex 3x-y=1$
$latex + \hspace{1cm} 5x+y=7$
___________________
$latex 8x=8$
Step 5: Solving for x, we have:
$latex x=1$
Step 6: Using the value $latex x=1$ in the second equation, we have:
$latex 5x+y=7$
$latex 5(1)+y=7$
$latex y=2$
The solution is $latex x=1,~~y=2$.
EXAMPLE 6
Solve the system of equations: $latex \begin{cases}2x-7y=1 \\ 2x+3y=11 \end{cases}$
Solution
Steps 1 and 2: The equations are now simplified and written in the form Ax+By=C.
Step 3: We multiply the second equation by -1 to obtain opposite coefficients in x:
$latex \begin{cases}2x-7y=1 \\ -2x-3y=-11 \end{cases}$
Step 4: Adding the equations, we have:
$latex 2x-7y=1$
$latex + \hspace{1cm} -2x-3y=-11$
___________________
$latex -10y=-10$
Step 5: Solving the equation, we have:
$latex y=1$
Step 6: Using the value $latex y=1$ in the first equation, we have:
$latex 2x-7y=1$
$latex 2x-7(1)=1$
$latex 2x=8$
$latex x=4$
The solution is $latex x=4,~~y=1$.
EXAMPLE 7
Solve the system of equations: $latex \begin{cases}3x-4y=5 \\ 6x-4y=2 \end{cases}$
Solution
Step 1: We can simplify the second equation by dividing it by 2:
$latex \begin{cases}3x-4y=5 \\ 3x-2y=1 \end{cases}$
Step 2: The equations are already in the form Ax+By=C.
Step 3: We multiply the second equation by -1 to obtain opposite coefficients in x:
$latex \begin{cases}3x-4y=5 \\ -3x+2y=-1 \end{cases}$
Step 4: We multiply the second equation by -1 to obtain opposite coefficients in x:
$latex 3x-4y=5$
$latex + \hspace{1cm} -3x+2y=-1$
___________________
$latex -2y=4$
Step 5: Solving the equation, we have:
$latex y=-2$
Step 6: Using the value $latex y=-2$ in the second equation, we have:
$latex 3x-2y=1$
$latex 3x-2(-2)=1$
$latex 3x+4=1$
$latex 3x=-3$
$latex x=-1$
The solution is $latex x=-1,~~y=-2$.
Systems of equations by elimination – Practice problems
Solve the system of equations: $latex \begin{cases}3x-2y=5 \\ 2x+y=8 \end{cases}$
Write the answer in the form x=?, y=?.
See also
Interested in learning more about systems of equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
