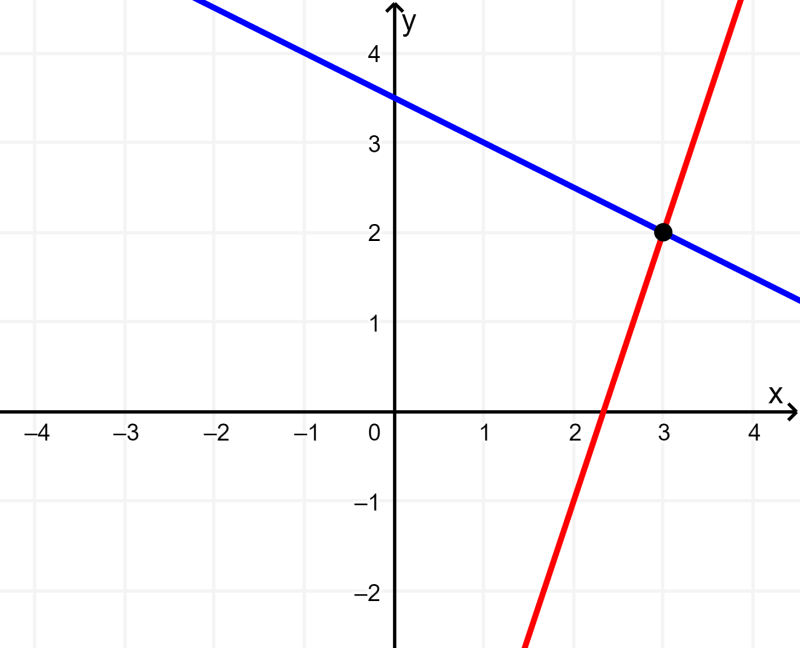
Apart from the substitution method and the elimination method, it is also possible to solve systems of equations using the graphical method. For this, we have to graph both linear equations and find the point of intersection.
In this article, we will look at a brief summary of the graphical method to solve systems of equations and then look at some examples with answers that use this method.
Summary of the graphing method for systems of equations
A system of equations is a system of two or more equations with two or more unknowns that have to be solved simultaneously.
A solution to a system of two equations with two variables is an ordered pair of numbers that makes both equations true.
Solving systems of two equations with the graphical method
To solve a system of two equations with two unknowns graphically we follow the following steps:
1. Graph the first equation using any method.
If you need help with this, you can check out our guide on how to graph linear functions.
2. Graph the second equation using the same coordinate system.
3. Find the point of intersection of the lines.
If the graphed lines intersect at a single point, the point of intersection represents the solution of the system. If the lines are parallel, they will never intersect and the system has no solution. If the lines are one on top of one another, we have an infinite number of solutions.
4. Check that the solution satisfies both equations.
Systems of equations by graphing – Examples with answers
EXAMPLE 1
Solve the system of equations graphically: $latex \begin{cases}y=3x-2 \\ y=-x+2 \end{cases}$
Solution
Step 1: Graph the first equation. The equation is written in the form $latex y=mx+b$, where m is the slope and b is the y-intercept. Therefore, the y-intercept is -2 and the slope is 3:
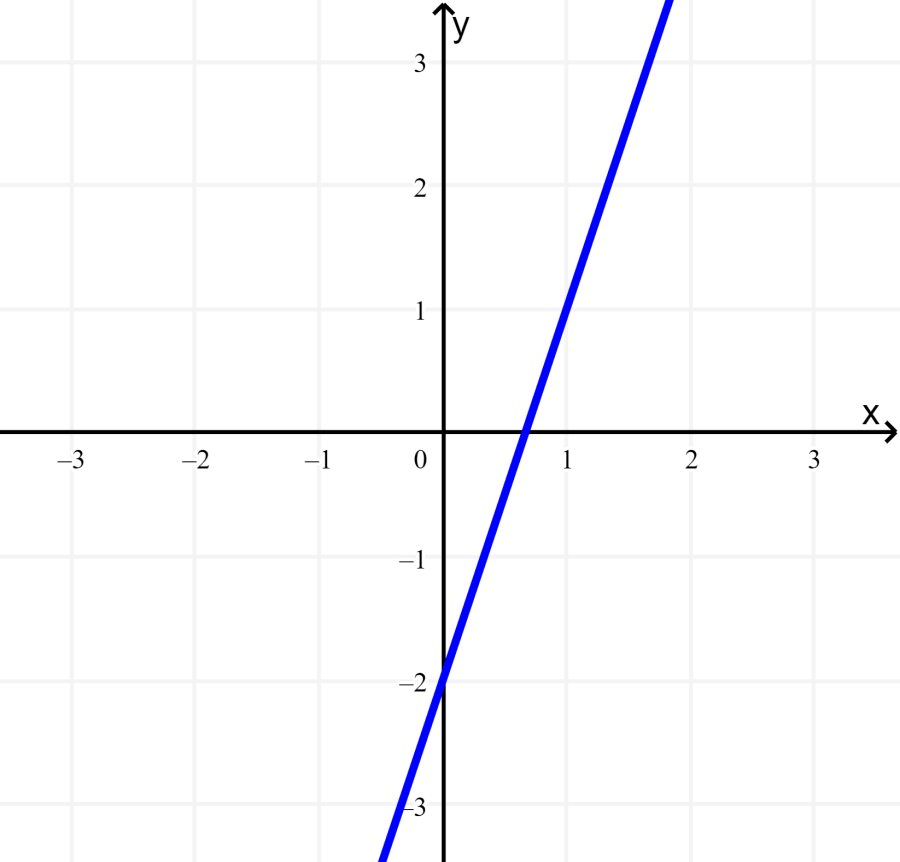
Step 2: To graph the second equation, we also use the slope-intercept form. Therefore, the y-intercept is 2, and the slope is -1:
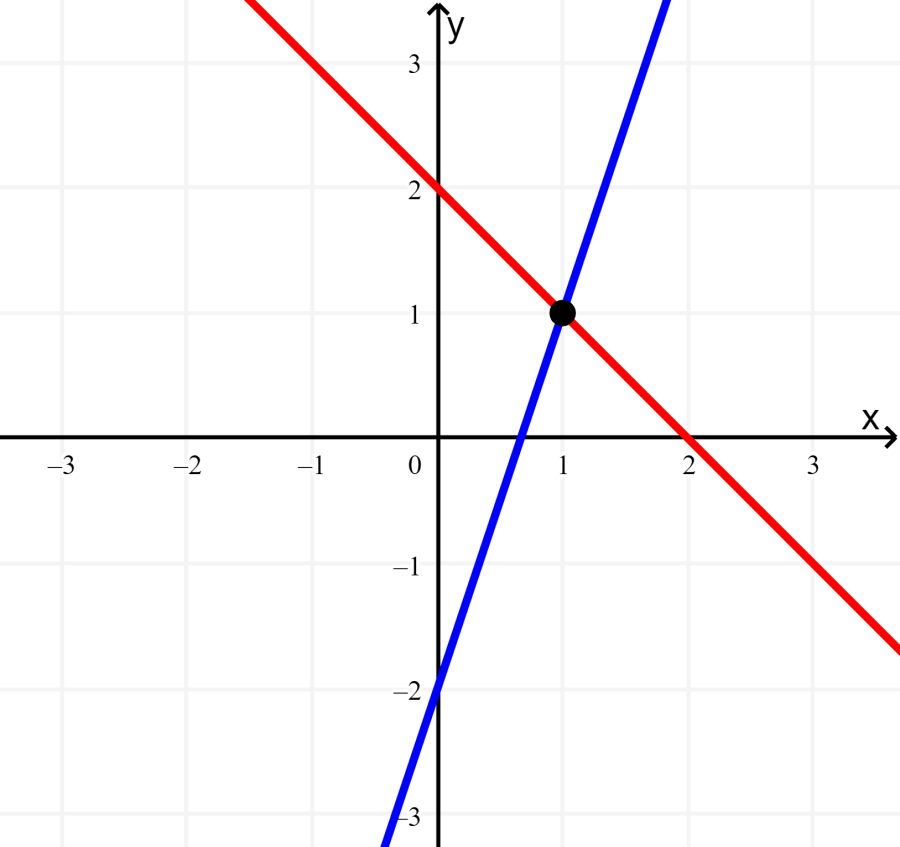
Step 3: To find the solution, we look for the point of intersection. We see that the equations intersect at the point (1, 1). Thus, the solution is $latex x=1, ~y=1$.
Step 4: We substitute the values of x=1and y=1 in both equations to check the answer:
$latex y=3x-2$
$latex 1=3(1)-2$
$latex 1=1$
$latex y=-x+2$
$latex 1=-1+2$
$latex 1=1$
EXAMPLE 2
Solve the system of equations graphically: $latex \begin{cases}2x+y=5 \\ x-y=4 \end{cases}$
Solution
Step 1: To graph the first equation, we rewrite it in the form $latex y=mx+b$:
$latex 2x+y=5$
$latex y=5-2x$
Therefore, the y-intercept is 5, and the slope is -2:
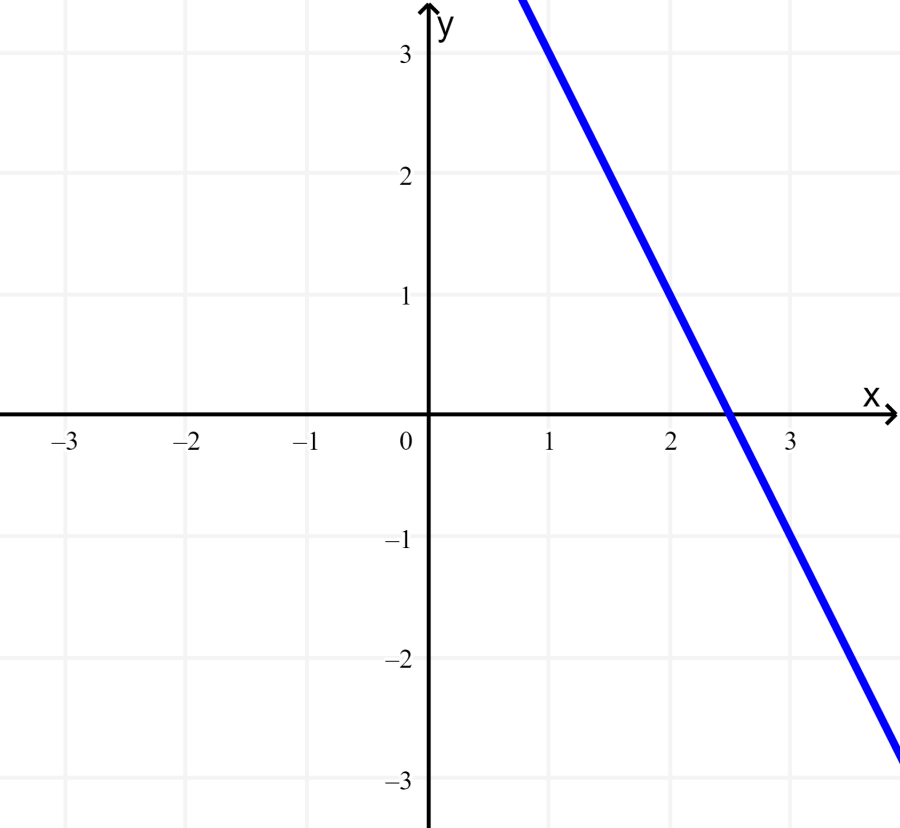
Step 2: We use the same method as the previous equation to graph the second equation:
$latex x-y=4$
$latex y=-4+x$
Therefore, the y-intercept is -4, and the slope is 1:
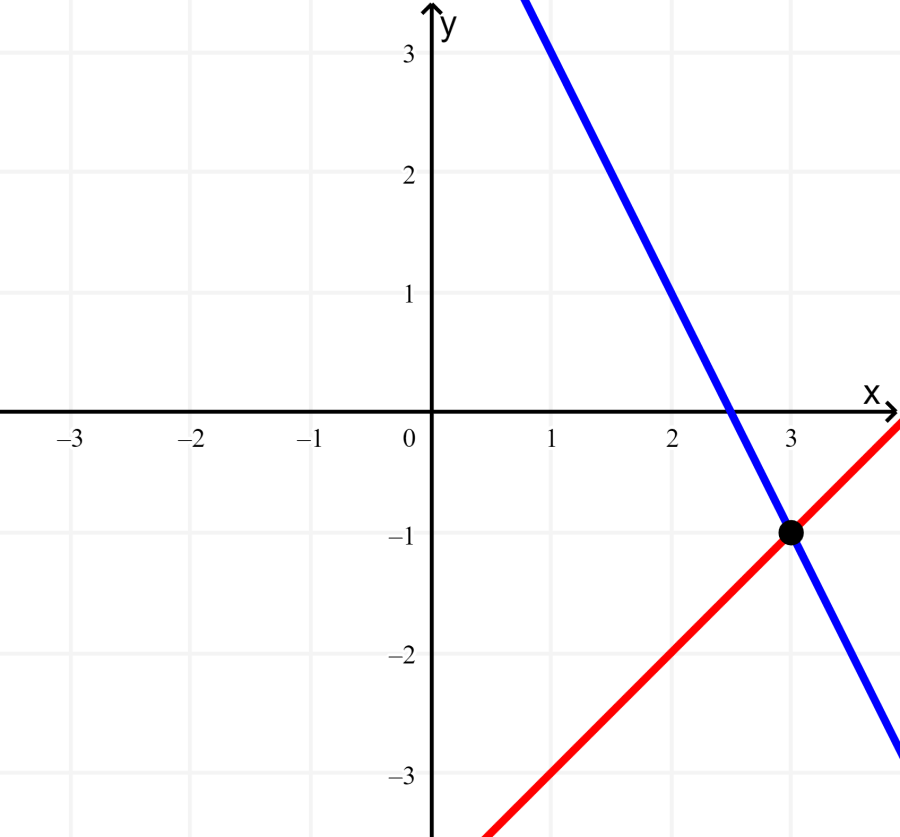
Step 3: In this case, we see that the equations intersect at the point (3, -1).
Step 4: We verify this solution by substituting the values of x = 3 and y = -1, in both equations:
$latex 2x+y=5$
$latex 2(3)+-1=5$
$latex 5=5$
$latex x-y=4$
$latex 3-(-1)=4$
$latex 4=4$
EXAMPLE 3
Solve the system of equations using the graphing method: $latex \begin{cases}2x+y=-1 \\ 4x+2y=-2 \end{cases}$
Solution
Step 1: We rewrite the first equation in the form $latex y=mx+b$:
$latex 2x+y=-1$
$latex y=-1-2x$
Here, the y-intercept is -1, and the slope is -2:
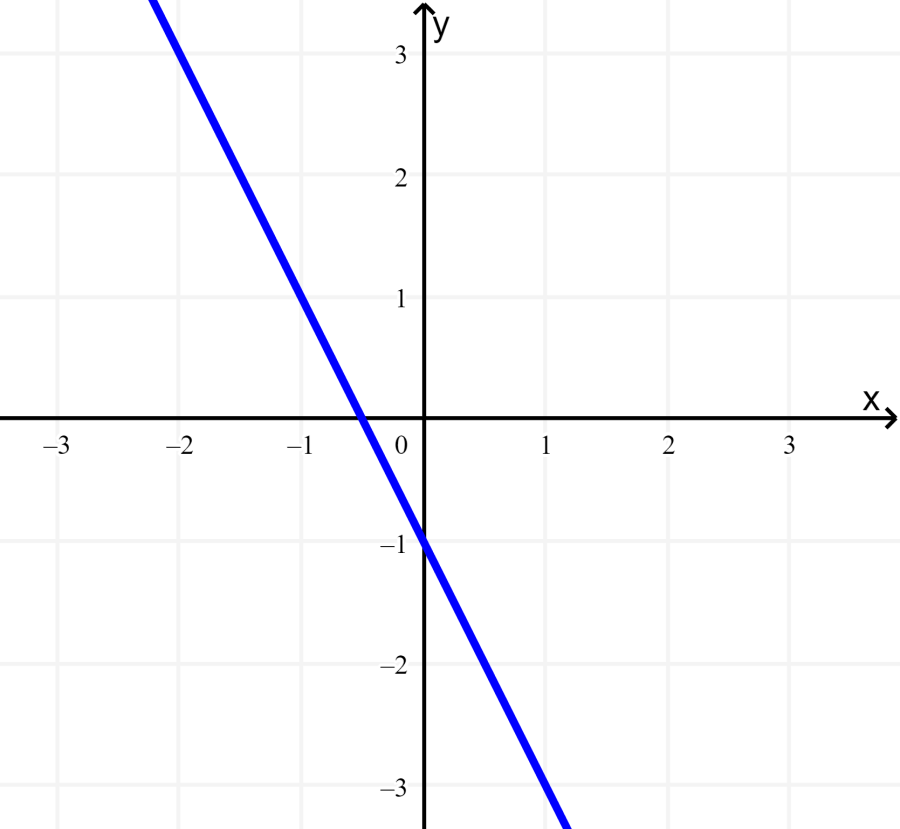
Step 2: Similarly, we rewrite the second equation to graph:
$latex 4x+2y=-2$
$latex y=-1-2x$
Thus, the y-intercept is -1, and the slope is -2:
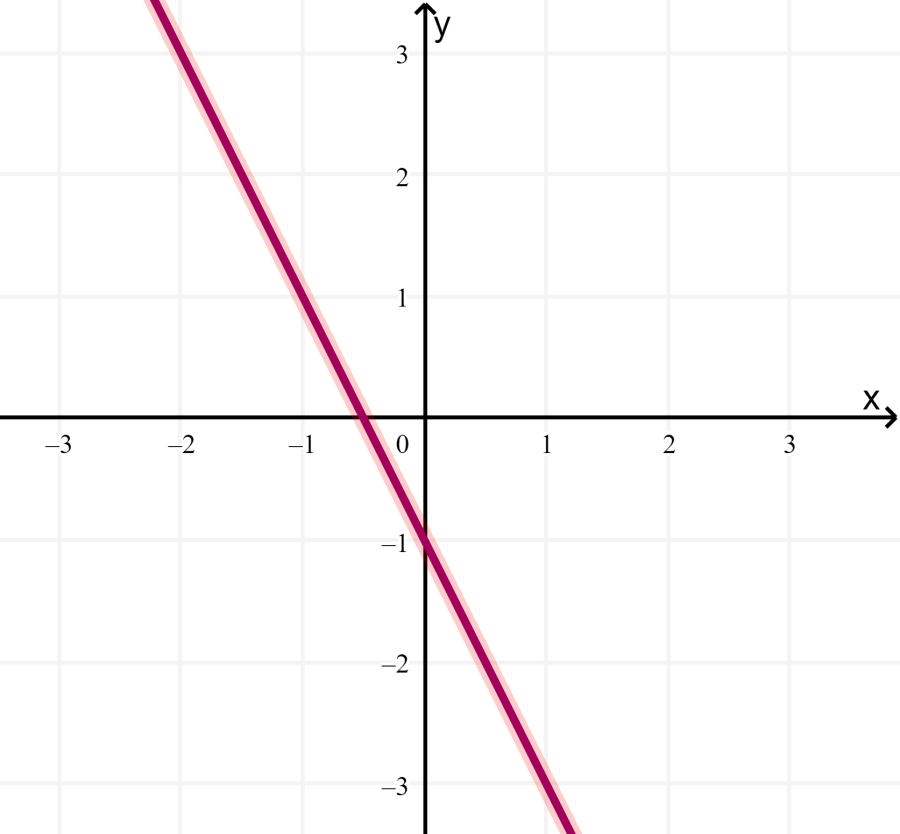
Step 3: In this case, we see that the equations overlap, so we have an infinite number of solutions.
EXAMPLE 4
Solve the system of equations using the graphing method: $latex \begin{cases}-3x+2y=-4 \\ 2x-y=3 \end{cases}$
Solution
Step 1: We rewrite the first equation in the form $latex y = mx + b$ to graph it:
$latex -3x+2y=-4$
$latex 2y=-4+3x$
$latex y=-2+\frac{3}{2}x$
Therefore, the y-intercept is -2, and the slope is $latex \frac{3}{2}$:
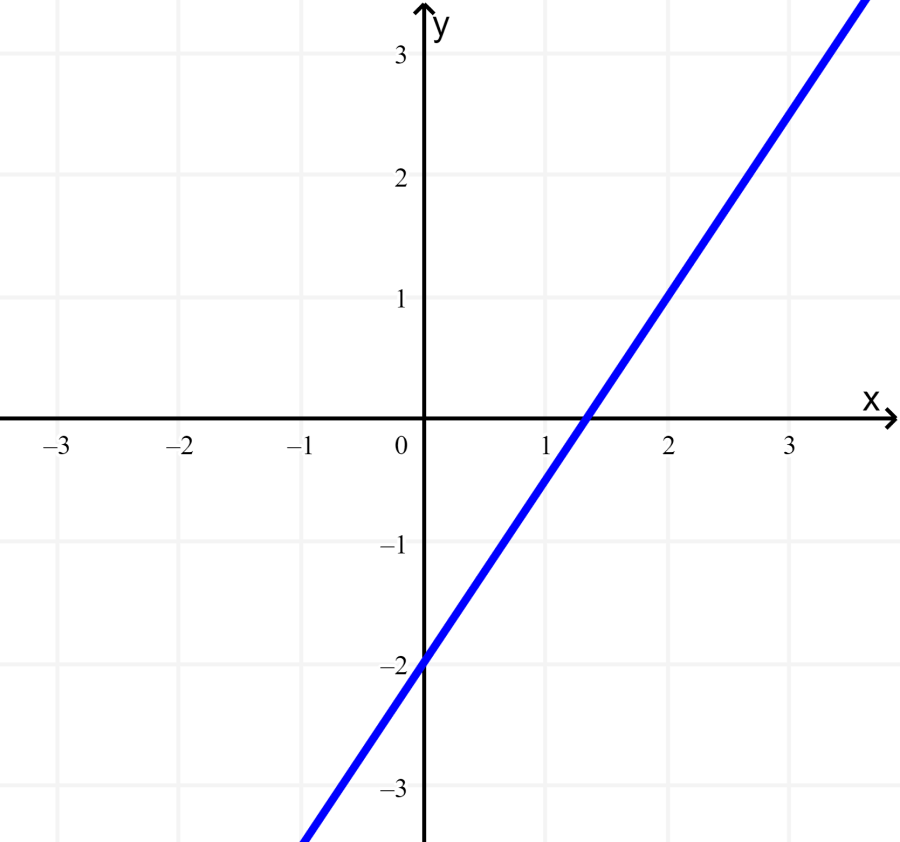
Step 2: We also rewrite the second equation to graph it:
$latex 2x-y=3$
$latex y=-3+2x$
Thus, the y-intercept is -3, and the slope is 2:
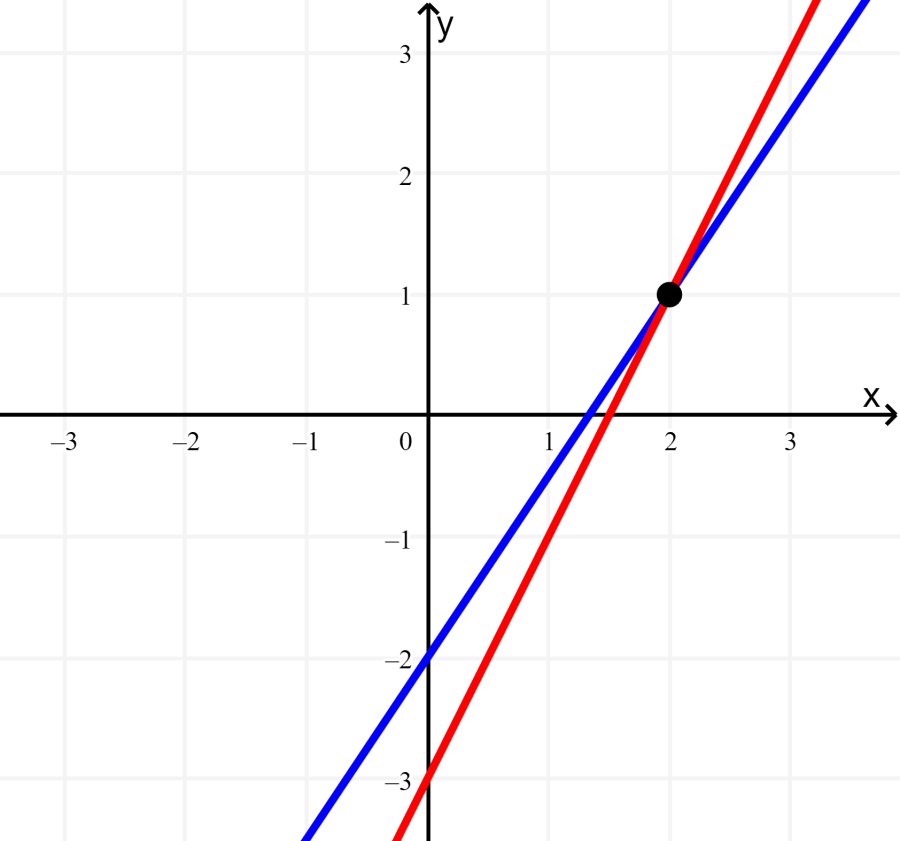
Step 3: We can see that the equations intersect at the point (2, 1).
Step 4: We substitute the values of x = 2 and y = 1 in both equations to check that we got the correct answer:
$latex -3x+2y=-4$
$latex -3(2)+2(1)=-4$
$latex -4=-4$
$latex 2x-y=3$
$latex 2(2)-1=3$
$latex 3=3$
EXAMPLE 5
Solve the system of equations using the graphing method: $latex \begin{cases}2x+3y=8 \\ x-2y=4 \end{cases}$
Solution
Step 1: We rewrite the first equation in the form $latex y=mx+b$:
$latex 2x+3y=8$
$latex 3y=8-2x$
$latex y=\frac{8}{3}-\frac{2}{3}x$
Therfore, the y-intercept is $latex \frac{8}{3}$, and the slope is $latex -\frac{2}{3}$:
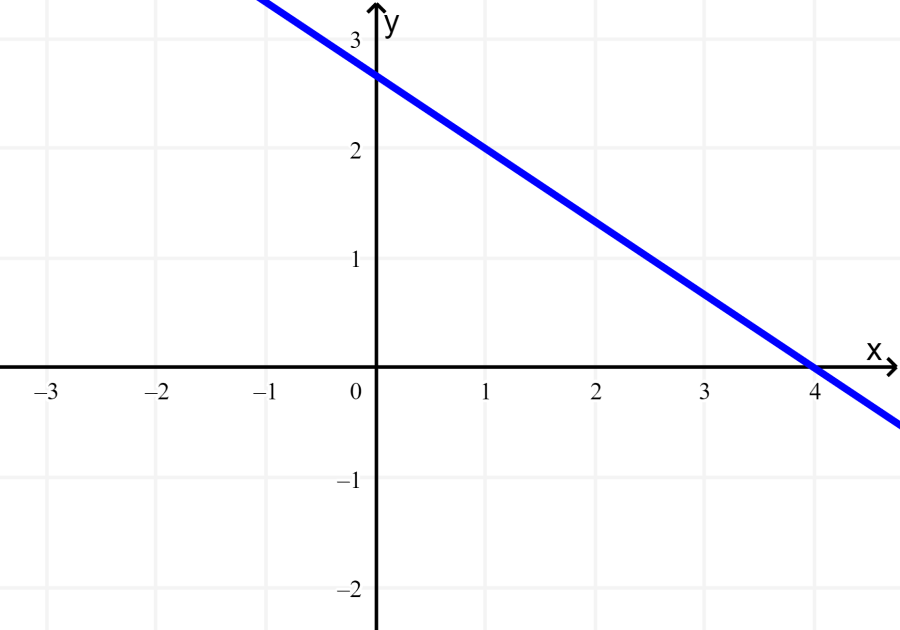
Step 2: We rewrite the second equation in the same way:
$latex x-2y=4$
$latex -2y=4-x$
$latex y=-2+\frac{1}{2}x$
Thus, the y -intercept is -2, and the slope is $latex \frac{1}{2}$:
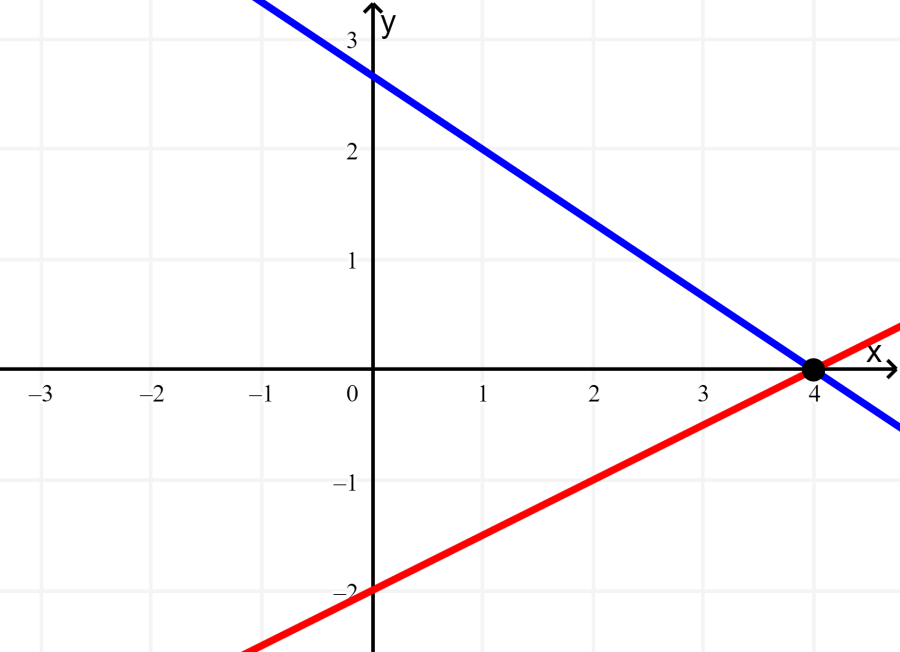
Step 3: Here, we see that the point of intersection is (4, 0).
Step 4: We verify this solution by substituting the values of x = 4 and y = 0, in both equations:
$latex 2x+3y=8$
$latex 2(4)+0=8$
$latex 8=8$
$latex x-2y=4$
$latex 4-0=4$
$latex 4=4$
System of equations by graphing – Practice problems
Use the graphic panel below to solve the systems of equations graphically.
Solve the system of equations using the graphical method $latex \begin{cases} -2x+3y=7 \\ 3x-y=7 \end{cases} $
Write the answer in the form x=?, y=?.
See also
Interested in learning more about linear equations and systems of equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
