Quadratic equations are algebraic equations that have the form ax²+bx+c=0. There are several methods that we can use to solve quadratic equations depending on the type of quadratic equation that we have. However, solving quadratic equations by the general quadratic formula is a method that always allows us to find both solutions to the equation.
In this article, we will take a look at a brief review of the general quadratic formula. Then we’ll learn how to solve quadratic equations with this formula and look at some practice problems.
ALGEBRA
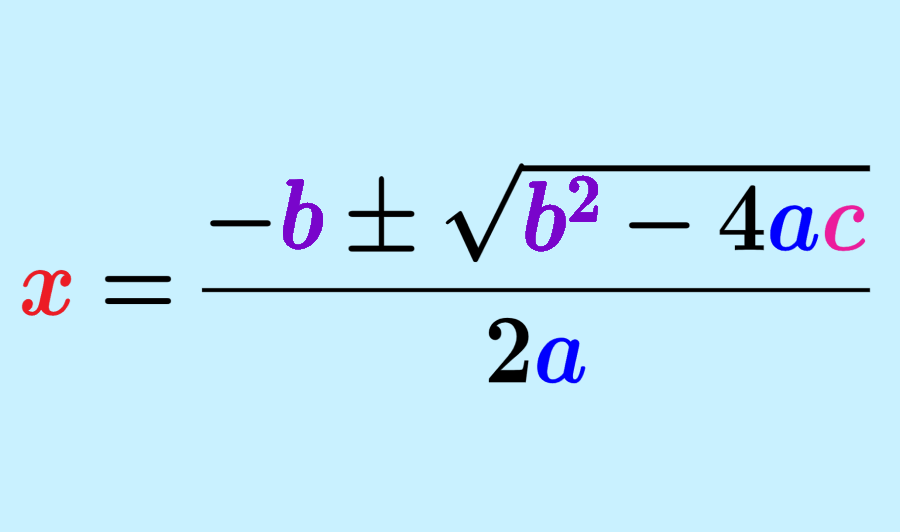
Relevant for…
Learning to solve quadratic equations using the quadratic formula.
ALGEBRA
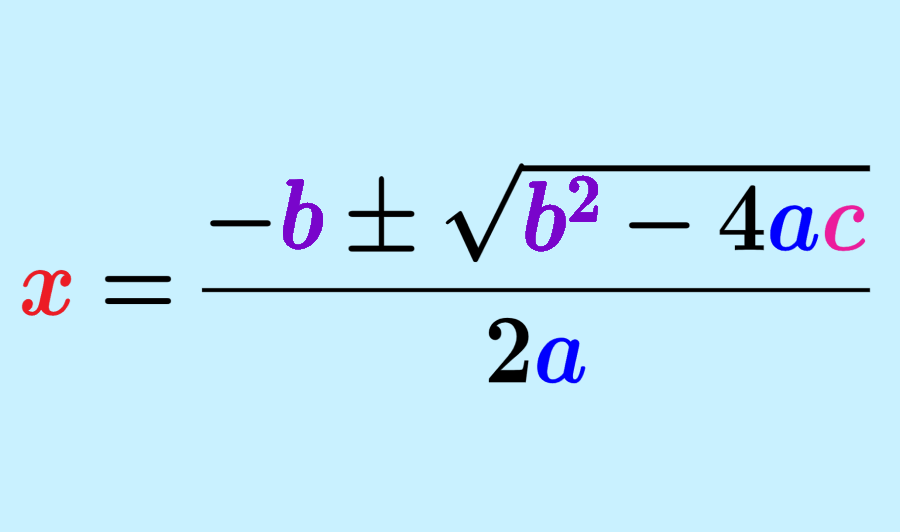
Relevant for…
Learning to solve quadratic equations using the quadratic formula.
How to solve quadratic equations using the quadratic formula?
To solve quadratic equations using the general quadratic formula, we start by writing the equation in the form $latex a{{x}^2}+bx+c=0$. Once we have the equation written in that form, we simply plug the coefficients a, b and c into the quadratic formula:
| $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$ |
Note: The ± sign is essential since it will allow us to obtain both solutions to the quadratic equation when it is the case.
The quantity that goes inside the square root sign, ie $latex b^2-4ac$ is called the discriminant of the quadratic equation.
The number of roots and the type of roots resulting from the quadratic equation depends on the value of the discriminant. Therefore, we have the following:
- If $latex b^2-4ac>0$, the equation has two real roots.
- If $latex b^2-4ac<0$, the equation has no real roots.
- If $latex b^2-4ac=0$, the equation has a repeated root.
In other words, if the value inside the square root is positive, we will have two real roots. If that value is negative, we won’t have any real roots (but we will have imaginary or complex roots). If that value is equal to zero, we have a single root.
If you want to know how to derive or prove the general quadratic formula, you can visit our article Quadratic Formula – Proof and Examples.
Quadratic equations with the quadratic formula – Examples with answers
The following examples are solved using the general quadratic formula. Each problem has its respective answer, but try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Find the solutions to the equation $latex {{x}^2}+3x-4=0$ using the quadratic formula.
Solution
Using the values $latex a=1$, $latex b=3$ and $latex c=-4$ in the formula, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(3)\pm \sqrt{( 3)^2-4(1)(-4)}}{2(1)}$$
$$=\frac{-3\pm \sqrt{9+16}}{2}$$
$$=\frac{-3\pm \sqrt{25}}{2}$$
$$=\frac{-3\pm 5}{2}$$
$$=\frac{-3-5}{2},~~\frac{-3+5}{2}$$
$$=\frac{-8}{2},~\frac{2}{2}=-4,~1$$
Therefore, the solutions are $latex x=-4$ and $latex x=1$.
EXAMPLE 2
Solve the equation $latex x^2-8x+4=0$, giving the answers to two decimal places.
Solution
We have the values $latex a=1$, $latex b=-8$, and $latex c=4$. Therefore, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-8)\pm \sqrt{( -8)^2-4(1)(4)}}{2(1)}$$
$$=\frac{8\pm \sqrt{64-16}}{2}$$
$$=\frac{8\pm \sqrt{48}}{2}$$
$$x=7.46 \text{ or } 0.54$$
The solutions are $latex x=7.46$ and $latex x=0.54$.
EXAMPLE 3
Using the general quadratic formula, show that the equation $latex 5x^2+4x+10=0$ has no real solutions.
Solution
Using the quadratic formula with the values $latex a=5$, $latex b=4$ and $latex c=10$, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(4)\pm \sqrt{( 4)^2-4(5)(10)}}{2(5)}$$
$$=\frac{-5\pm \sqrt{16-200}}{10}$$
$$=\frac{-5\pm \sqrt{-184}}{10}$$
We have a negative number inside the square root. $latex \sqrt{-184}$ is not a real number, so the equation has no real roots.
EXAMPLE 4
Solve the equation $latex x^2-10x+25=0$ using the quadratic formula.
Solution
We use the values $latex a=1$, $latex b=-10$ and $latex c=25$ in the quadratic formula and we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-10)\pm \sqrt{( -10)^2-4(1)(25)}}{2(1)}$$
$$=\frac{10\pm \sqrt{100-100}}{2}$$
$$=\frac{10\pm \sqrt{0}}{2}$$
$$=\frac{10}{2}$$
$$=5$$
In this case, we have a repeated root $latex x=5$.
EXAMPLE 5
Find the solutions to the equation $latex x^2+2x-1=0$ by expressing them to two decimal places.
Solution
Using the quadratic formula with $latex a=1$, $latex b=2$ and $latex c=-1$, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(2)\pm \sqrt{( 2)^2-4(1)(-1)}}{2(1)}$$
$$=\frac{-2\pm \sqrt{4+4}}{2}$$
$$=\frac{-2\pm \sqrt{8}}{2}$$
$$x=-2.41 \text{ or }0.41$$
The solutions are $latex x=-2.41$ and $latex x=0.41$.
EXAMPLE 6
Solve the equation $latex 2x^2+3x-4=0$ using the general formula. Express the solutions to two decimal places.
Solution
We have the values $latex a=2$, $latex b=3$, and $latex c=-4$. Therefore, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(3)\pm \sqrt{( 3)^2-4(2)(-4)}}{2(2)}$$
$$=\frac{-3\pm \sqrt{9+32}}{4}$$
$$=\frac{-3\pm \sqrt{41}}{2}$$
$$=-2.35 \text{ or }0.85$$
The solutions of the equation are $latex x=-2.35$ and $latex x=0.85$.
EXAMPLE 7
What are the solutions to the equation $latex 3x^2+x-3=0$ to two decimal places?
Solution
Using the values $latex a=3$, $latex b=1$ and $latex c=-3$ in the quadratic formula, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(1)\pm \sqrt{( 1)^2-4(3)(-3)}}{2(3)}$$
$$=\frac{-1\pm \sqrt{1+36}}{6}$$
$$=\frac{-1\pm \sqrt{37}}{6}$$
$$x=-1.18\text{ or }0.85$$
The solutions of the equation are $latex x=-1.18$ and $latex x=0.85$.
Quadratic equations with the quadratic formula – Practice problems
Solve the following problems using the general quadratic formula. Click “Check” to make sure that your answer is correct.
See also
Interested in learning more about quadratic equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
