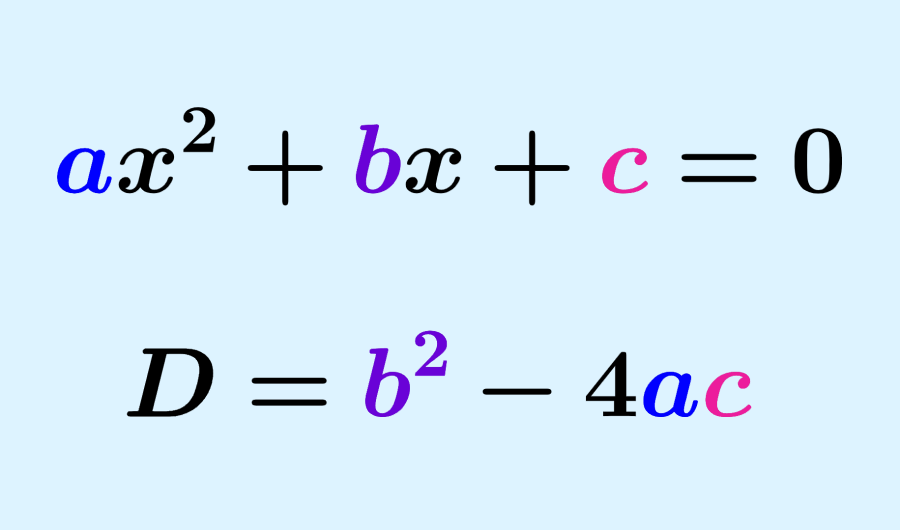Quadratic equations are algebraic equations that have the form ax²+bx+c=0. Considering this form, the discriminant of a quadratic equation is the value b²-4ac. This value goes inside the square root of the general quadratic formula and determines the type of solutions that we will have.
In this article, we will learn everything related to the discriminant of a quadratic equation. In addition, we will use its formula to solve some practice problems.
Formula for the discriminant of a quadratic equation and applications
When we have quadratic equations written in the form $latex a{{x}^2}+bx+c=0$, the discriminant is given by the following formula:
| $latex D=b^2-4ac$ |
The value of the discriminant gives us information about the type of roots that we will get by solving a given quadratic equation. Namely, we have the following:
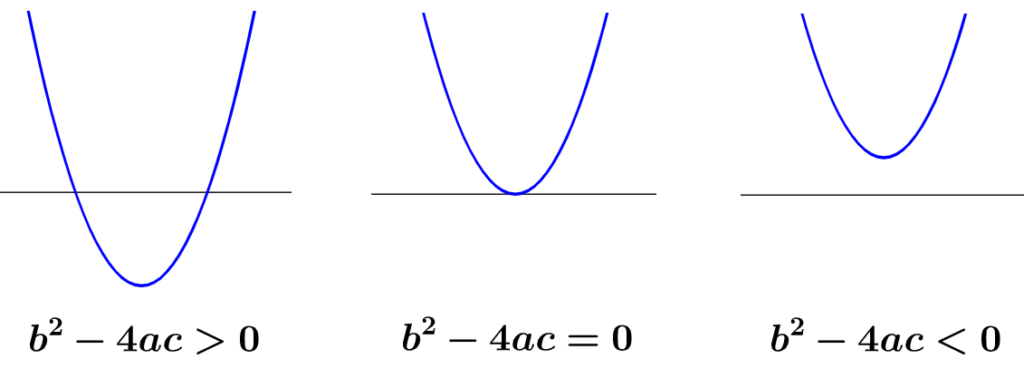
- When $latex b^2-4ac>0$, the quadratic equation has two real roots.
- When $latex b^2-4ac<0$, the quadratic equation has no real roots.
- When $latex b^2-4ac=0$, the quadratic equation has a repeated root.
We can understand this better if we remember that the general quadratic formula, which allows us to solve any quadratic equation, is the following:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
Therefore, we can see that the discriminant is the expression inside the square root of the general formula. This means that, when the value inside the square root is positive, we will have two real roots.
On the other hand, when the value inside the square root is negative, we won’t have any real roots (but we will have imaginary or complex roots). And finally, if the discriminant is equal to zero, we will have a single repeated root.
The discriminant of a quadratic equation indicates whether the graph of the quadratic equation intersects the x-axis at two different points, does not intersect the x-axis, or touches the x-axis at only one point, as we see in the following diagram:
Discriminant of a quadratic equation – Examples with answers
The formula for the discriminant of a quadratic equation is used to solve the following examples. Each example has its respective solution, but try to solve the problems yourself.
EXAMPLE 1
Find the discriminant of the equation $latex x^2+4x+5=0$.
Solution
Using the values $latex a=1$, $latex b=4$ and $latex c=5$ in the formula for the discriminant, we have:
$latex D=b^2-4ac$
$latex D=4^2-4(1)(5)$
$latex D=16-20$
$latex D=-4$
The discriminant of the equation is $latex D=-4$.
EXAMPLE 2
Determine the discriminant of the equation $latex -2x^2+4x-2$.
Solution
We have the values $latex a=-2$, $latex b=4$, and $latex c=-2$. Using these values in the formula for the discriminant, we have:
$latex D=b^2-4ac$
$latex D=4^2-4(-2)(-2)$
$latex D=16-16$
$latex D=0$
The discriminant of the equation is $latex D=0$.
EXAMPLE 3
Use the discriminant to show that the equation $latex 5x^2+4x+10=0$ has no real solutions.
Solution
Using the discriminant formula with the values $latex a=5$, $latex b=4$ and $latex c=10$, we have:
$latex D=b^2-4ac$
$latex D=4^2-4(5)(10)$
$latex D=16-200$
$latex D=-184$
The discriminant is negative, so the equation has no real roots. This is because we have a negative number inside the square root of the general quadratic formula.
EXAMPLE 4
How many real roots does the equation $latex -3x^2-2x+5=0$ have?
Solution
We use the values $latex a=-3$, $latex b=-2$ and $latex c=5$ in the formula for the discriminant, and we have:
$latex D=b^2-4ac$
$latex D=(-2)^2-4(-3)(5)$
$latex D=4+60$
$latex D=64$
The discriminant is positive, so the equation has two real roots.
EXAMPLE 5
Find the value of k in the equation $latex 3x^2-6x+k=0$, assuming that the equation has only one repeated root.
Solution
In this case, we have $latex a=3$, $latex b=-6$, and $latex c=k$. To find the value of k, we have to use the formula for the discriminant that has a value equal to zero, since the equation has only one root:
$latex D=b^2-4ac=0$
$latex (-6)^2-4(3)(k)=0$
$latex 36-12k=0$
$latex -12k=-36$
$latex k=3$
Therefore, if the quadratic equation has a single repeated root, the value of k is 3.
EXAMPLE 6
Find the value of k in the equation $latex kx^2+5x-4=0$ if the equation has only one root.
Solution
We have the values $latex a=k$, $latex b=5$ and $latex c=-4$. We use the formula for the discriminant, set it equal to zero, and solve for k:
$latex D=b^2-4ac=0$
$latex (5)^2-4(k)(-4)=0$
$latex 25+16k=0$
$latex 16k=-25$
$latex k=-\frac{25}{16}$
Therefore, if the quadratic equation has a single repeated root, the value of k is 25/16.
EXAMPLE 7
Prove that $latex y=2x^2+7x+7$ is always positive by using the discriminant.
Solution
Using the values $latex a=2$, $latex b=7$ and $latex c=7$ in the formula for the discriminant, we have:
$latex D=b^2-4ac$
$latex D=(7)^2-4(2)(7)$
$latex D=49-56$
$latex D=-7$
Since the discriminant is negative, the equation has no real roots. Then, the function does not cut the x-axis. Also, since the coefficient of $latex x^2$ is positive, the graph of the function opens up and is always above the x-axis, so the values are always positive.
Discriminant of a quadratic equation – Practice problems
Use the formula for the discriminant of a quadratic equation to solve the following practice problems.
See also
Interested in learning more about quadratic equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
