The order of operations are the rules that tell us which operations should be performed first when we have multiple operations in an expression. The order of operations tells us that we have to start with parentheses, then exponents, then multiplication and division, and finally addition and subtraction.
Here, we will learn about the order of operations in detail. We will explore the acronym PEMDAS, and we will apply it to solve some practice problems.
ALGEBRA
Relevant for…
Learning the correct order of operations to avoid incorrect answers.
ALGEBRA
Relevant for…
Learning the correct order of operations to avoid incorrect answers.
What is the order of operations?
The order of operations are the rules which tell us the sequence in which multiple operations in an expression must be solved.
In math, operations mean things like add, subtract, multiply, divide, etc. Performing individual operations is very easy, but when we have something like the following expression, it can get a bit confusing:
$latex 2+\left( {{{4}^{2}}-2\times 3} \right)$
Where do we start? The answer to this is to use the order of operations:
1. Perform operations inside parentheses or other grouping signs:
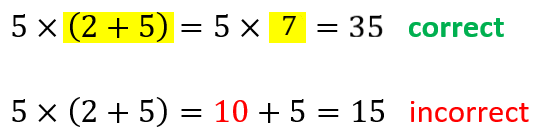
2. Solve for exponents (powers, roots) before multiplying, dividing, adding, or subtracting:
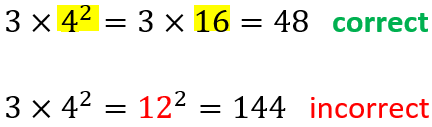
3. Multiply or divide before adding or subtracting:
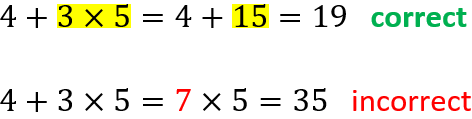
4. Solve the additions and subtractions from left to right:
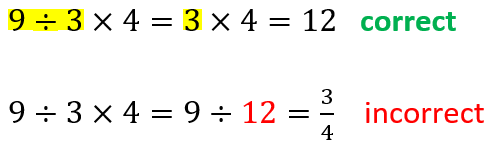
PEMDAS acronym
One way to easily remember the order of operations is PEMDAS, where each letter represents a mathematical operation:
P Parentheses
E Exponents
M Multiplication
D Division
A Addition
S Subtraction
STEPS
1. We start with parentheses and other grouping signs.
2. We solve exponents, that is, roots and powers.
3. Since multiplication and division are on the same level, we solve from left to right.
4. Since additions and subtractions are on the same level, we solve from left to right.
Why follow the order of operations?
We must apply the order of mathematical operations to solve expressions correctly so that we always arrive at the same correct answer.
The following is an example of how we can get wrong answers if we don’t use PEMDAS:
Expression solved from left to right
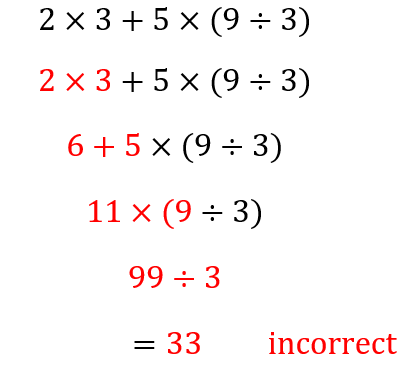
Expression solved using the order of operations
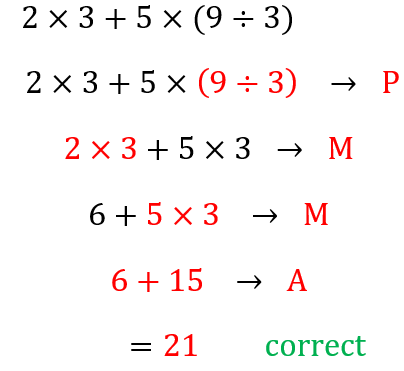
Examples of the order of operations
Try to solve the examples yourself and look at the process used carefully to master the use of PEMDAS.
EXAMPLE 1
What is the result of $latex 5+4\times 3 -8$?
Solution
The order of operations tells us that we have to solve multiplication and division before addition and subtraction.
Also, when we have two or more operations of the same type, we solve from left to right. Therefore, we have:
$latex 5+4\times 3 -8$
$latex =5+12 -8$
$latex =17-8$
$latex =9$
EXAMPLE 2
Find the result of $latex (4+8)-3\times 3-4$.
Solution
We solve the operation of the parentheses first, then the multiplication, and we finish with the additions and subtractions:
$latex (4+8)-3\times 3-4$
$latex =(12)-3\times 3-4$
$latex =12-9-4$
$latex =-1$
EXAMPLE 3
Solve the following $latex 3+{{3}^{2}}\left( {3+4} \right)$.
Solution
We use PEMDAS to solve as follows:
$latex 3+{{3}^{2}}\left( {3+4} \right)$
$latex =3+{{3}^{2}}\left( 7 \right)$
$latex =3+9\left( 7 \right)$
$latex =3+63$
$latex =66$
EXAMPLE 4
Use PEMDAS to solve $latex \left( {3+4\times 3} \right)-{{2}^{2}}$.
Solution
By applying PEMDAS, we can solve as follows:
$latex \left( {3+4\times 3} \right)-{{2}^{2}}$
$latex =\left( {3+12} \right)-{{2}^{2}}$
$latex =15-{{2}^{2}}$
$latex =15-4$
$latex =11$
EXAMPLE 5
Find the result of $latex 10\times \left( {4+2} \right)+{{3}^{2}}\left( {3+4} \right)\div 3$.
Solution
We apply PEMDAS to solve:
$latex 10\times \left( {4+2} \right)+{{3}^{2}}\left( {3+4} \right)\div 3$
$latex =10\times 6+{{3}^{2}}\left( {3+4} \right)\div 3$
$latex =10\times 6+{{3}^{2}}\left( 7 \right)\div 3$
$latex =10\times 6+9\left( 7 \right)\div 3$
$latex =60+9\left( 7 \right)\div 3$
$latex =60+63\div 3$
$latex =60+21$
$latex =81$
You can find more solved examples of the order of operations by visiting our article: Order of Operations – Examples and Practice Problems
Order of operations – Practice problems
What is the result of the following? $$5(2^2+3)-4+6(5-2)^2+2\times 5$$
Write the answer in the input box.
See also
Interested in learning more about algebraic expressions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
