We can perform various operations with algebraic expressions. These operations include addition, subtraction, multiplication, and division. In this article, we will learn how to perform these four operations with algebraic expressions.
We will look at several examples with answers to fully understand the main ideas.
ALGEBRA
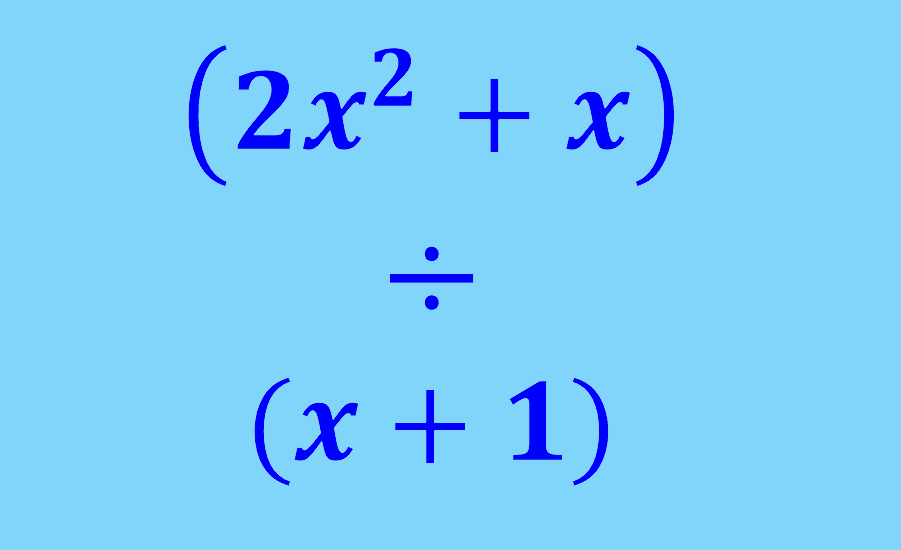
Relevant for…
Performing addition, subtraction, multiplication and division with algebraic expressions.
ALGEBRA
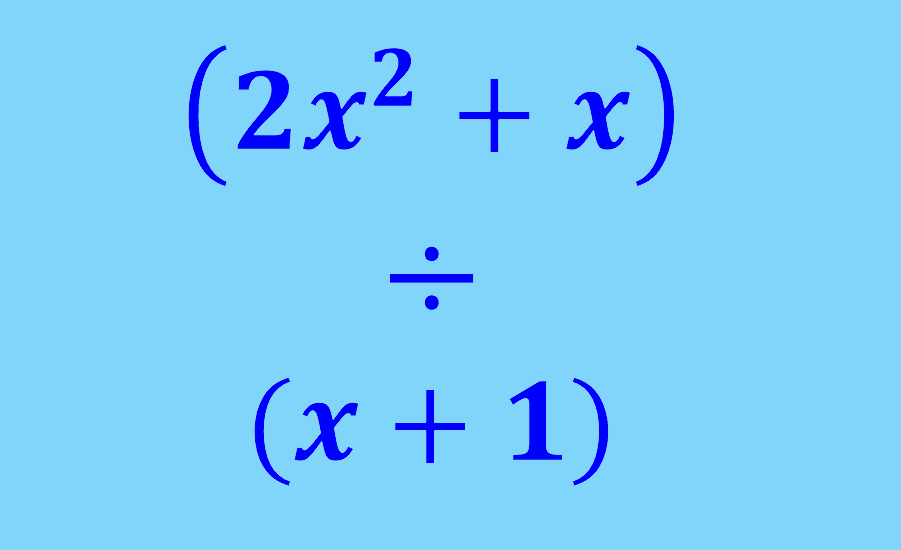
Relevant for…
Performing addition, subtraction, multiplication and division with algebraic expressions.
Order of operations
Operations with algebraic expressions follow a certain order. Every time you see an algebraic expression or an equation, decompose it in the order in which it has to be solved. To easily remember this order, consider this acronym: PEMDAS:
1. Evaluate all expressions within parentheses or other grouping symbols.
2. Evaluate all expressions that contain exponents.
3. Do the remaining multiplications and divisions as you come across them. That is, multiply and divide from left to right.
4. Solve the remaining additions and subtractions as you come across them. That is, add and subtract from left to right.
EXAMPLES
- Solve the expression $latex 5+4\times 3$.
Solution: Applying the order of operations:
$latex 5+4\times 3=5+12=17$
- Solve the expression $latex 2\left( {3+1} \right)+2\times 3\left( {3+1} \right)$.
Solution: Applying the order of operations:
$$2\left( {3+1} \right)+2\times 3\left( {3+1} \right)=2\left( 4 \right)+2\times 3\left( 4 \right)$$
$latex =8+2\times 12$
$latex =8+24$
$latex =32$
Try solving the following exercise
Addition and subtraction
In addition or subtraction of algebraic expressions, it is important that the terms are like terms. Like terms are defined as the same variables raised to the same power.
EXAMPLES
- Add the expressions $latex 2x+4$ and $latex 3x+2$.
Solution: Identify and combine like terms:
$latex 2x+4+3x+2=5x+6$
- Add the expressions $latex 2{{x}^{2}}+3x+4$ and $latex 4{{x}^{2}}-2x+3$ .
Solution: Identify and combine like terms:
$latex 2{{x}^{2}}+3x+4+4{{x}^{2}}-2x+3$
$latex =6{{x}^{2}}+x+7$
- Substract the expression $latex 3x+3$ from the expression $latex 8x+5$.
Solution: Given that we have a subtraction, we have to change the sign of the expression being subtracted:
$$8x+5-(3x+3)=8x+5-3x-3$$
$latex =5x+2$
- Substract the expression $latex 2{{x}^{2}}+3x-6$ from the expression $latex -4{{x}^{2}}+2x-5$.
Solution: Given that we have a subtraction, we have to change the sign of the expression being subtracted:
$latex -4{{x}^{2}}+2x-5-\left( {2{{x}^{2}}+3x-6} \right)$
$latex =-4{{x}^{2}}+2x-5-2{{x}^{2}}-3x+6$
$latex =-6{{x}^{2}}-x+1$
Try solving the following exercise
Multiplication of algebraic expressions
To multiply algebraic expressions, we have to use the distributive property. The distributive property indicates that for any real numbers a, b, c, we have:
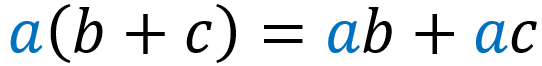
EXAMPLES
- Multiply $latex x$ by $latex x+1$.
Solution: We have to use the distributive property and distribute the $latex x$:
$latex x\left( {x+1} \right)=x\times x+x\times 1$
$latex ={{x}^{2}}+x$
- Multiply $latex x+2$ by $latex x+1$.
Solution: We have to use the distributive property twice. We distribute the $latex x$, and then the 2:
$$(x+2)(x+1)={{x}^{2}}+x+2x+2$$
$latex ={{x}^{2}}+3x+2$
- Multiply $latex x+4$ by $latex {{x}^{2}}+2x-5$.
Solution: We have to use the distributive property twice. We distribute the $latex x$, and then the 4:
$latex (x+4)({{x}^{2}}+2x-5)$
$$={x}^{3}+2{{x}^{2}}-5x+4{{x}^{2}}+8x-20$$
$latex ={{x}^{3}}+6{{x}^{2}}+3x-20$
- Multiply $latex x-3$ by $latex 2{{x}^{2}}-2x+3$.
Solution: We have to use the distributive property twice. We distribute the $latex x$, and then the -3:
$latex (x-3)(2{{x}^{2}}-2x+3)$
$$=2{x}^{3}-2{{x}^{2}}+3x-6{{x}^{2}}+6x-9$$
$latex ={2{x}^{3}}-8{{x}^{2}}+9x-12$
Try solving the following exercise
Division
Dividing an algebraic expression is similar to simplifying terms. The numerical coefficients are divided and the exponents of the variables are subtracted.
EXAMPLES
- Divide the expression $latex 6{{a}^{2}}{{b}^{3}}$ by $latex 2{{a}^{3}}{{b}^{2}}$.
Solution: In order to understand more easily, we write the division as follows:
$$\frac{{6aa~bbb}}{{2~aaa~bb}}$$
We divide the constants and simplify the variables:
$$=\frac{{3b}}{a}$$
- Solve the following:
$$\frac{{\left( {x+1} \right)\left( {x+2} \right)}}{{\left( {x+2} \right)\left( {x-3} \right)}}$$
Solution: We simplify the algebraic expression by canceling the terms:
$$\frac{{x+1}}{{x-3}}$$
- Simplify the expression $latex \frac{3}{x}+\frac{4}{{x+1}}$.
Solution: To simplify, the equation needs to have the same denominator. Here, we multiply both terms by $latex x\left( {x+1} \right)$ and simplify:
$$\frac{{3\left( x \right)\left( {x+1} \right)}}{x}=3\left( {x+1} \right)$$
$$\frac{{4\left( x \right)\left( {x+1} \right)}}{{x+1}}=4x$$
Combining the terms and simplifying, we have:
$$3\left( {x+1} \right)+4x=3x+3+4x$$
$latex =7x+3$
Try solving the following exercise
See also
Interested in learning more about algebraic expressions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
