Prime and composite numbers are the two types of numbers that differ based on the number of factors they have. Prime numbers are only divisible by 1 and themselves. On the other hand, composite numbers have more than two factors.
In this article, we will learn about prime and composite numbers in detail. We will use examples and a grid to easily identify the numbers.
ALGEBRA
Relevant for…
Learning to differentiate between prime numbers and composite numbers.
ALGEBRA
Relevant for…
Learning to differentiate between prime numbers and composite numbers.
What are prime numbers?
Prime numbers are numbers that only have two possible divisors. These numbers are only divisible by 1 and themselves. This means that if we try to divide the number by any number other than 1 or itself, we will get a remainder.
What are composite numbers?
Composite numbers are the numbers that are divisible by 1, by themselves, and also by other numbers. These numbers have more than two possible divisors.
Let’s look at examples of prime and composite numbers:
The 7 can be written as the multiplication of 1 and 7, but it cannot be written as any other multiplication of natural numbers. 7 only has factors 1 and 7, so it is a prime number.
12 can be written as the multiplication of 1 and 12, as well as the multiplications of 2 and 6, 3 and 4. Since 12 is divisible by more numbers than 1 and itself, 12 is a composite number.
Is 1 a prime number?
It is reasonable to think that if 1 can only be divided by 1 and by itself, then 1 is prime. However, 1 is not considered a prime number, since it actually only has one divisor. The criterion “an integer is prime only if it has two positive divisors” is used in this argument.
Is 1 a composite number?
1 is not a composite number, since it cannot be formed as the product of prime numbers. This means that the number 1 is neither prime nor composite.
What is the importance of prime numbers?
Prime numbers are the basis of arithmetic since any number consists of a product formed from a series of these numbers.
Prime numbers are very relevant in many areas because they have important properties for factoring. One such property is that, while it is easy to find large primes, it is inevitably difficult to factor large numbers back into primes.
It’s one thing to find that 20 equals (2×2×5), but it’s quite another to find that 2,244,354 is (2 × 3 × 7 × 53,437). It is for this reason that prime numbers are vital in electronic communications. Most modern computer cryptography works using prime factors of large numbers.
Primes are important to mathematicians because they are the bases of integers, and they are important to computation because their strange mathematical properties make them perfect for our current uses of encryption.
Examples of prime and composite numbers
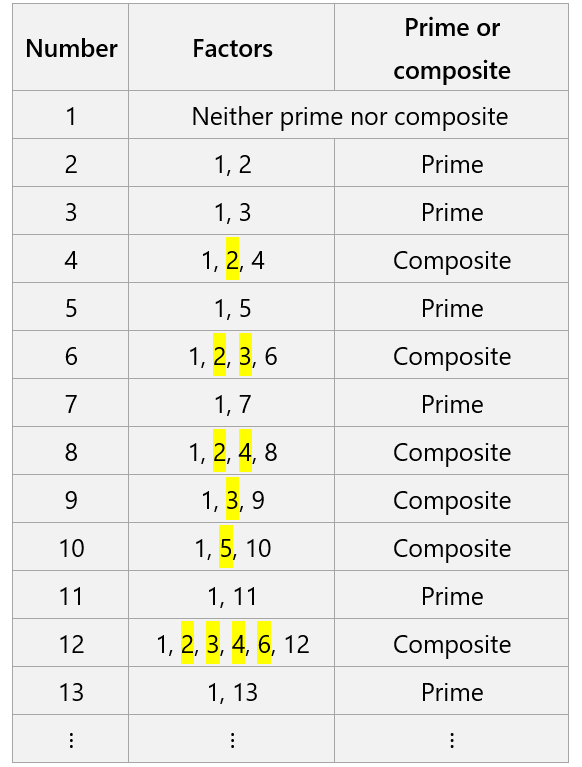
In the table below, we have the numbers 1 through 13 along with their divisors. Divisors other than 1 and the same number are highlighted.
This means that the numbers that have numbers highlighted are composites.
Prime and composite numbers – Practice problems
We can use the following problems to better understand prime numbers:
- Is 4 a prime number?
No, since its factors are 1, 2, and 4.
- Is 5 a prime number?
Yes, since its factors are 1 and 5.
- Is 10 a prime number?
No, because its factors are 1, 5, and 10.
With this, you can determine if a certain number is prime or not.
See also
Interested in learning more about prime numbers or algebraic expressions? Look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
