The prime numbers up to 200 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73 , 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
In this article, we will learn about prime numbers. We will start with a description of prime numbers. Then, we will look at some of their most important properties. Also, we will use a table to understand how we can find prime numbers.
What is the definition of prime numbers?
Prime numbers are defined as positive integers that have exactly two factors. Numbers that have more than two factors are called composite numbers.
If we have that p is a prime number, then by definition it only has two factors, which are 1 and p.
The first ten prime numbers
The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
EXAMPLES
- The number 6 is not a prime number because it has the factors 1, 2, 3, and 6.
- The number 7 is a prime number since it only has the factors 1 and 7.
- The number 16 is not a prime number since it has the factors 1, 2, 4, 8, and 16.
- The number 17 is a prime number since it only has the factors 1 and 17.
Is 1 considered a prime number?
1 is not a prime number since all prime numbers are defined as positive integers that only have two factors.
The number 1 only has one factor which is itself, therefore, 1 is not considered a prime number. If 1 were to be considered a prime number, we would have to redefine some mathematical properties.
Keep in mind that 1 is not a composite number either since it has no other factors apart from itself.
Prime numbers up to 100
We are going to find all the prime numbers up to 100 with the help of the following table. We will cross out the non-prime numbers step by step.
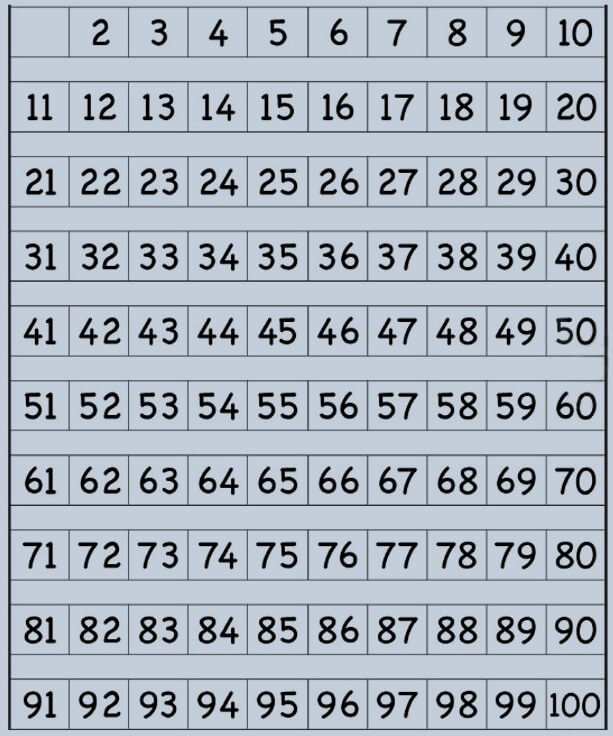
Let’s start with 2. 2 is a prime number, but all multiples of 2 will be composite numbers since they are divisible by 2. Then, we cross out all multiples of 2 from the table.
The next prime number is 3. In the same way, all multiples of 3 will be composite since they are divisible by 3, so we cross them out.
After 3 we have 5. We cross out all multiples of 5 since they are composite numbers.
Then, we have the prime number 7 and we cross out all its multiples.
The next prime number is 11, so we cross out all its multiples 22, 33, 44, 55, 66, 77, 88, 99. All these numbers have already been crossed out, so we finish crossing out all the composite numbers.
This is the list of prime numbers up to 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 , 73, 79, 83, 89, 97.
You don’t need to memorize all of these numbers, but it would be helpful if you memorize small prime numbers like 2, 3, 5, 7, 11, 13
Prime numbers up to 200
Since we have already obtained a list with the first prime numbers up to 100, now we can form a list with the prime numbers from 1 to 200:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
Important properties of prime numbers
The following are some of the most important properties of prime numbers:
- Each of the numbers greater than 1 can be divided by at least one prime number without leaving a remainder.
- All positive integers greater than 2 can be expressed as the sum of two prime numbers.
- All prime numbers are odd, except for 2. Therefore, 2 is the only prime number that is even.
- All composite numbers can be factored into prime factors, and they are all unique.
Examples of prime numbers
The following are some examples to determine whether a number is prime or not:
EXAMPLES
- Determine whether 35 is prime or not
Answer: The factors of 35 are 1, 5, 7, 35. 35 has more than two factors, therefore it is not prime.
- Determine whether 37 is prime or not
Answer: The factors of 37 are 1 and 37. 37 has exactly two factors, so it is prime.
- Determine whether 45 is prime or not
Answer: The factors of 45 are 1, 3, 5, 9, 15, and 45. 45 has more than two factors, so it is not prime.
- Determine whether 41 is prime or not
Answer: The factors of 41 are 1 and 41. 41 has exactly two factors, so it is prime.
Frequent questions
How can I find prime numbers?
We can determine whether a number is prime or not by dividing it by 2, 3, 5, 7, and 11. If we do not get a remainder by dividing by these numbers, then the number is not prime.
Can we have negative prime numbers?
No, we cannot have negative prime numbers. One definition of prime numbers is that prime numbers are numbers greater than 1 that have exactly two factors.
How many factors does a prime number have in total?
In total, a prime number has exactly two factors, itself and 1.
What is the largest known prime number?
The largest known prime number as of November 2022 is 282,589,933 − 1. These numbers are found using computers and numerical methods.
See also
Interested in learning more about prime numbers? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
