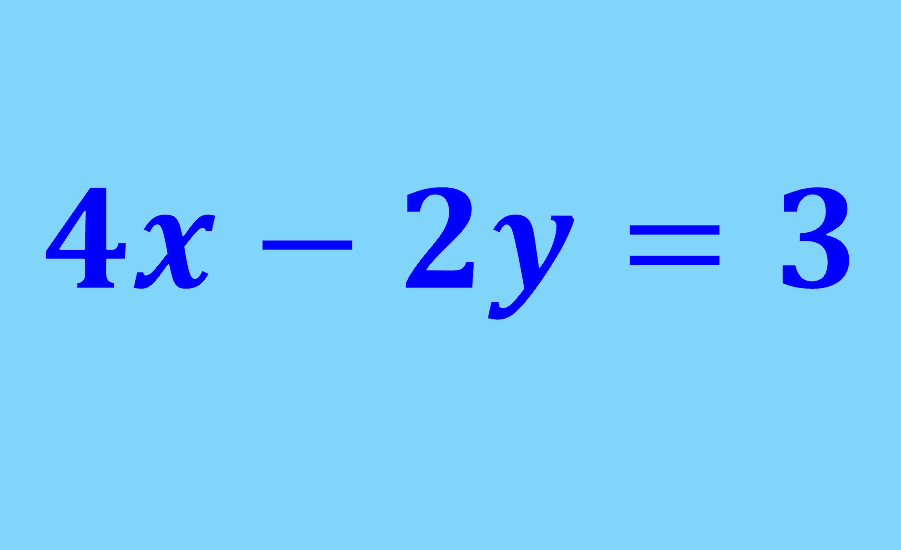Linear equations with two variables are equations that have two variables that are not raised to any power. An example of an equation with two variables is x+2y=5. These equations can only be solved if we know the value of one of the variables. Otherwise, the equation has an infinite number of solutions.
In this article, we will become familiar with solving linear equations in two variables with worked examples to help us understand the concepts.
Steps to solve equations with two variables
The following are the steps we can take to solve a linear equation with two variables.
If you want to learn how to solve systems of equations with two variables, you can visit this article: Solving Linear Systems of Equations – Methods and Examples.
1. Substitute the value of a variable into the equation.
If we know the value of a variable, we plug it into the given equation. If we don’t know the value of a variable, the equation automatically has an infinite number of solutions.
2. Simplify both sides of the equation.
- Remove the parentheses (using the distributive property) if there are any.
- Remove the fractions (we multiply by the least common multiple).
- Simplify like terms.
3. Isolate the variable on one side of the equation.
We perform operations to move the variable to one side of the equation and the constants to the other side.
4. Solve for the variable.
For example, if we have $latex 4x=8$, we divide both sides by 4 to get $latex x=2$.
5. Check your result.
Substitute the values of the variables into the original equation to check that we get a correct equation.
Examples of linear equations with two variables
EXAMPLE 1
If the value of y is equal to 5, find the value of x in the equation $latex 3x-4y=10$.
Solution
Step 1: Substitute: We have that $latex y=5$, therefore:
$latex 3x-4y=10$
$latex 3x-4(5)=10$
$latex 3x-20=10$
Step 2: Simplify: We have nothing to simplify:
Step 3: Solve for the variable: We add 20 to both sides:
$latex 3x-20=10$
$latex 3x-20+20=10+20$
$latex 3x=30$
Step 4: Solve: We divide both sides by 3:
$$\frac{3x}{3}=\frac{30}{3}$$
$latex x=10$
EXAMPLE 2
We have that the value of y is equal to -3. Solve the equation $latex -3x+5y=-6$ for x.
Solution
Step 1: Substitute: We have that $latex y=-3$, therefore:
$latex -3x+5y=-6$
$latex -3x+5(-3)=-6$
$latex -3x-15=-6$
Step 2: Simplify: We do not have like terms.
Step 3: Solve for the variable: We add 15 to both sides:
$latex -3x-15+15=-6+15$
$latex -3x=9$
Step 4: Solve: We divide both sides by -3:
$$\frac{-3x}{-3}=\frac{9}{-3}$$
$latex x=-3$
EXAMPLE 3
If we have $latex y=2$, find the value of $latex x$ in the equation $latex 2x+4y=10-x+7$.
Solution
1. Substitute the value of the variable into the equation:
$latex 2x+4(2)=10-x+7$
$latex 2x+8=10-x+7$
2. Simplify:
- We don’t have parentheses.
- We don’t have fractions.
- We combine like terms: $latex 2x+8=17-x$.
3. Isolate the variable: we move the 8 to the right and the –x to the left:
$latex 2x+8-8=17-x-8$
$latex 2x=9-x$
$latex 2x+x=9-x+x$
$latex 3x=9$
4. Solve for $latex x$: we divide both sides by 3:
$$\frac{3}{3}x=\frac{{9}}{3}$$
$$x=\frac{{9}}{3}=3$$
5. Check the answer: substitute the values of the variables in the original equation:
$latex 2(3)+4(2)=10-(3)+7$
$latex 6+8=10-3+7$
$latex 14=14$
This is true.
Answer: $latex y=2, x=3$.
EXAMPLE 4
If we have $latex x=4$, find the value of $latex y$ in the equation $latex 5x-2y+5=12-3x+15$.
Solution
1. Substitute the value of the variable:
$$5(4)-2y+5=12-3(4)+15$$
$latex 20-2y+5=12-12+15$
2. Simplify:
- We don’t have parentheses.
- We don’t have fractions.
- We combine like terms: $latex 25-2y=15$.
3. Isolate the variable: we move the 25 to the right:
$latex 25-2y-25=15-25$
$latex -2y=-10$
4. Solve for $latex y$ completely: we divide both sides by-2:
$$\frac{-2}{-2}y=\frac{{-10}}{-2}$$
$$y=\frac{{-10}}{-2}=5$$
5. Check the answer: substitute the values of the variables in the original equation:
$$5(4)-2(5)+5=12-3(4)+15$$
$latex 20-10+5=12-12+15$
$latex 15=15$
This is true.
Answer: $latex y=5, x=4$.
EXAMPLE 5
If the value of x is equal to -2, solve the equation $latex 4y+2(2y+3)=3x-4$ for y.
Solution
Step 1: Substitute: We have that $latex x=-2$, therefore:
$latex 4y+2(2y+3)=3(-2)-4$
$latex 4y+2(2y+3)=-6-4$
Step 2: Simplify: We expand the parentheses and combine like terms:
$latex 4y+2(2y+3)=-6-4$
$latex 4y+4y+6=-10$
$latex 8y+6=-10$
Step 3: Solve for the variable: We subtract 6 from both sides:
$latex 8y+6-6=-10-6$
$latex 8y=-16$
Step 4: Solve: We divide both sides by 8:
$$\frac{8y}{8}=\frac{16}{-8}$$
$latex y=-2$
EXAMPLE 6
Find the value of $latex x$ and $latex y$ in the equation $latex 3x-2y=20+x$.
Solution
We have no given value of any variable, so this equation has an infinite number of solutions. For example, suppose $latex x=1$, then we would have:
$latex 3x-2y=20+x$
$latex 3(1)-2y=20+1$
$latex 3-2y=21$
$latex -2y=21-3$
$latex -2y=18$
$latex y=-9$
Now, suppose that $latex x=2$, then we would have:
$latex 3x-2y=20+x$
$latex 3(2)-2y=20+2$
$latex 6-2y=22$
$latex -2y=22-6$
$latex -2y=16$
$latex y=-8$
We could continue with different values of $latex x$ and we would always get different answers. This means that there are an infinite number of solutions.
EXAMPLE 7
If we have $latex x=6$, find the value of $latex y$ in the equation $latex x+4(y+2)=10+2y+2x$.
Solution
1. Substitute the value of the variable:
$latex 6+4(y+2)=10+2y+2(6)$
$latex 6+4(y+2)=10+2y+12$
2. Simplify:
- Simplify parentheses: $latex 6+4y+8=10+2y+12$.
- We don’t have fractions.
- Combine like terms: $latex 4y+14=2y+22$.
3. Isolate the variable: we move the 14 to the right and the 2y to the left:
$latex 4y+14-14=2y+22-14$
$latex 4y=2y+8$
$latex 4y-2y=2y+8-2y$
$latex 2y=8$
4. Solve for $latex y$: we divide both sides by 2:
$$\frac{2}{2}y=\frac{{8}}{2}$$
$$y=\frac{{8}}{2}=4$$
5. Verify the answer: we substitute the values of the variables in the original equation:
$$6+4(4+2)=10+2(4)+2(6)$$
$latex 6+4(6)=10+8+12$
$latex 30=30$
This is true
Answer: $latex y=4, x=6$
EXAMPLE 8
If the value of z equals 5, solve the equation $latex 4y+2z=2(3y+10)+z-11$ for y.
Solution
Step 1: Substitute: We substitute $latex z=5$ in the equation:
$$4y+2(5)=2(3y+10)+5-11$$
$$4y+10=2(3y+10)+5-11$$
Step 2: Simplify: We expand the parentheses and combine like terms:
$latex 4y+10=6y+20+5-11$
$latex 4y+10=6y+14$
Step 3: Solve for the variable: We subtract 10 and 6 y from both sides:
$latex 4y+10-10=6y+14-10$
$latex 4y=6y+4$
$latex 4y-6y=6y+4-6y$
$latex -2y=4$
Step 4: Solve: We divide both sides by -2:
$$\frac{-2y}{-2}=\frac{4}{-2}$$
$latex y=-2$
EXAMPLE 9
If we have $latex y=2$, find the value of $latex x$ in the equation $latex \frac{1}{3}x+2y+\frac{1}{2}x=y+x+1 $.
Solution
1. Substitute the value of the variable:
$$\frac{1}{3}x+2(2)+\frac{1}{2}x=2+x+1$$
$$\frac{1}{3}x+4+\frac{1}{2}x=2+x+1$$
2. Simplify:
- We don’t have parentheses.
- Simplify fractions: multiply by 6: $latex 2x+24+3x=12+6x+6$.
- Combine like terms: $latex 5x+24=18+6x$.
3. Isolate the variable: we move the 24 to the right and the 6x to the left:
$latex 5x+24-24=18+6x-24$
$latex 5x=6x-6$
$latex 5x-6x=6x-6-6x$
$latex -x=-6$
4. Solve for $latex x$: we divide both sides by-1:
$$\frac{-1}{-1}x=\frac{{-6}}{-1}$$
$$x=\frac{{-6}}{-1}=6$$
5. Check the answer: substitute the values of the variables in the original equation:
$$\frac{1}{3}(6)+2(2)+\frac{1}{2}(6)=(2)+(6)+1$$
$latex 2+4+3=2+6+1$
$latex 9=9$
This is true.
Answer: $latex y=2, x=6$
EXAMPLE 10
If the value of y is equal to -3, solve the equation $latex \frac{y+1}{2}+2x=2(2y+6)+x+2$ for x.
Solution
Step 1: Substitute: We have that $latex y=-3$, therefore:
$$\frac{-3+1}{2}+2x=2(2(-3)+6)+x+2$$
$$\frac{-3+1}{2}+2x=2(-6+6)+x+2$$
Step 2: Simplify: We combine like terms and simplify:
$$\frac{-2}{2}+2x=2(0)+x+2$$
$latex -1+2x=x+2$
Step 3: Solve for the variable: We add 1 and subtract x from both sides:
$latex -1+2x+1=x+2+1$
$latex 2x=x+3$
$latex 2x-x=x+3-x$
$latex x=3$
Step 4: Solve: We have already found the solution:
$latex x=3$
EXAMPLE 11
Solve the equation $latex 2x+2y=3x+10$ for y.
Solution
Step 1: Substitute: In this case, we do not have any given value, so automatically, the equation has an infinite number of solutions. For example, suppose we have $latex x = 0$, then we would have:
$latex 2x+2y=3x+10$
$latex 2(0)+2y=3(0)+10$
$latex 2y=10$
$latex y=5$
If we now have $latex x = 1$, we have:
$latex 2x+2y=3x+10$
$latex 2(1)+2y=3(1)+10$
$latex 2+2y=3+10$
$latex 2+2y=13$
$latex 2y=15$
$latex y=15/2$
We could continue with different values and each time we would get different results, so by not having a specified value of a variable, the equation has infinite solutions.
Linear equations with two variables – Practice problems


If x=7, what is the value of y in $latex 4(x+8)-2y=3y+10$?
Write the answer in the input box.
See also
Interested in learning more about equations? Take a look at these pages: