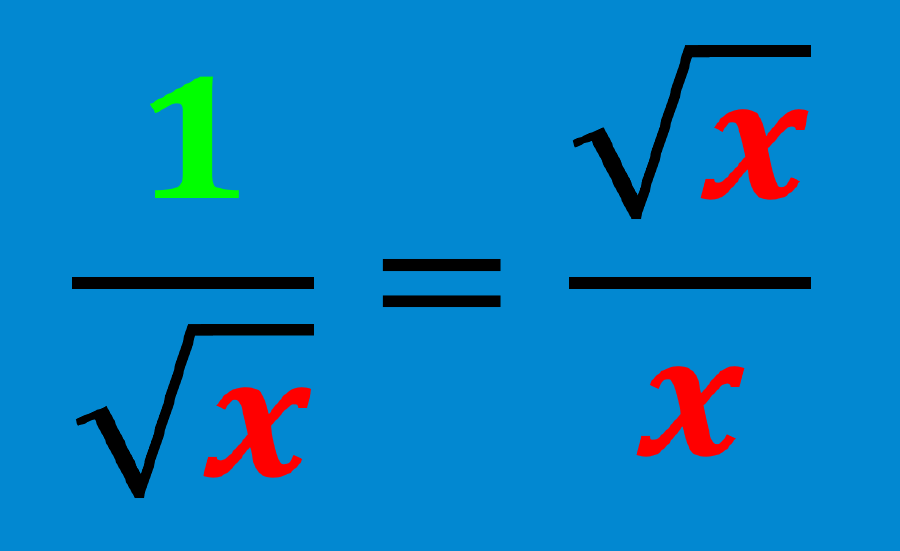Expressions that have radicals, that is, square roots, cube roots, or others in the denominator, can be rationalized to remove those radicals from the denominator. There are two main types of rationalization that we can apply depending on whether the denominator is a monomial or a binomial.
We will look at these two types of rationalizations along with examples to facilitate understanding.
What is rationalization of denominators?
Rationalization of denominators refers to the process of eliminating any radicals in the denominator such as square roots, cube roots, or others. The main idea is to multiply the original fraction by an appropriate value so that after simplifying, the denominator no longer has any radicals.
The idea of rationalizing a denominator perhaps makes more sense if we consider the definition of rationalization. Remember that the numbers 4, $latex \frac{1}{3}$ and 0.75 are known as rational numbers, that is, these numbers can be expressed as a ratio of two whole numbers $latex \frac{4}{1}, ~\frac{1 }{3}$ and $latex \frac{3}{4}$ respectively.
Some radicals are irrational since they cannot be represented as the ratio of two whole numbers. Therefore, the objective of rationalizing the denominator is to change the expression so that the denominator becomes a rational number.
Rationalization of denominators with one term
Let’s start with the fraction $latex \frac{1}{{\sqrt{3}}}$. Its denominator is $latex {\sqrt{3}}$, which is an irrational number. This makes it difficult to find the exact value of $latex \frac {1}{{\sqrt{3}}}$.
We know that it is possible to multiply this fraction by 1 without changing its value. We also know that $latex \frac{{\sqrt{3}}}{{\sqrt{3}}}$ is equal to 1, so we can multiply by that expression:
$latex \frac{1}{{\sqrt{3}}}\times \frac{{\sqrt{3}}}{{\sqrt{3}}}$
$latex =\frac{{\sqrt{3}}}{{\sqrt{{3\times 3}}}}$
$latex =\frac{{\sqrt{3}}}{{\sqrt{9}}}$
$latex =\frac{{\sqrt{3}}}{3}$
The denominator of the fraction is no longer a radical.
We decided to multiply by $latex \frac{{\sqrt{3}}}{{\sqrt{3}}}$ because we know that the square root of a number multiplied by itself will equal a whole number. We have the expression $latex \sqrt{x}\times \sqrt{x}=x$.
Therefore, to rationalize expressions that have only one term that is a radical in the denominator, we multiply both the denominator and the numerator by that radical and simplify. We can look at this in the following examples.
EXAMPLE 1
Rationalize the denominator of the expression $latex \frac{4}{{\sqrt{2}}}$.
Solution: We see that the denominator contains a radical expression, the square root of 2. We eliminate the radical by multiplying the denominator by itself, but in order not to affect the expression, we also multiply the numerator. Therefore, we multiply by the expression $latex \frac{{\sqrt{2}}}{{\sqrt{2}}}$:
$latex \frac{4}{{\sqrt{2}}}\times \frac{{\sqrt{2}}}{{\sqrt{2}}}$
$latex =\frac{{4\sqrt{2}}}{{\sqrt{4}}}$
Now, we can simplify the radical in the denominator and simplify the resulting fraction if possible:
$latex =\frac{{4\sqrt{2}}}{2}$
$latex =2\sqrt{2}$
EXAMPLE 2
Rationalize the denominator of the expression $latex \frac{5}{{\sqrt{3}}}$.
Solution: In this case, we have the square root of 3 in the denominator. To rationalize, we multiply the denominator and the numerator by the square root of 3. Then, we multiply by the expression $latex \frac{{\sqrt{3}}}{{\sqrt{3}}}$:
$latex \frac{5}{{\sqrt{3}}}\times \frac{{\sqrt{3}}}{{\sqrt{3}}}$
$latex =\frac{{5\sqrt{3}}}{{\sqrt{9}}}$
Now, we can simplify the radical in the denominator:
$latex =\frac{{5\sqrt{3}}}{3}$
In this case, we can no longer simplify.
EXAMPLE 3
Simplify by rationalizing the denominator of the expression $latex \frac{{5\sqrt{{10}}}}{{\sqrt{2}}}$.
Solution: Similar to the previous problems, we multiply by the expression $latex \frac{{\sqrt{2}}}{{\sqrt{2}}}$:
$latex \frac{{5\sqrt{{10}}}}{{\sqrt{2}}}\times \frac{{\sqrt{2}}}{{\sqrt{2}}}$
$latex =\frac{{5\sqrt{{20}}}}{{\sqrt{4}}}$
Now, we can simplify the radical in the denominator. But we also note that we can rewrite the radical in the numerator to simplify:
$latex =\frac{{5\sqrt{{4\times 5}}}}{2}$
$latex =\frac{{5\times 2\sqrt{5}}}{2}$
$latex =5\sqrt{5}$
Try solving the following practice problems
How many cases of rationalization of denominators are there?
We can distinguish two more important cases of rationalization of denominators based on the number of terms that the expression has in the denominator. The rationalization of denominators with one term that we saw earlier is a case of rationalization of denominators.
| Irrational | Rational | |
| $latex \frac{1}{{\sqrt{3}}}$ | = | $latex \frac{{\sqrt{3}}}{3}$ |
| $latex \frac{{3+\sqrt{2}}}{{\sqrt{2}}}$ | = | $latex \frac{{3\sqrt{2}+2}}{2}$ |
Additionally, we also have the rationalization of denominators with two terms or also known as rationalization of denominators with binomials.
| Irrational | Rational | |
| $latex \frac{4}{{\sqrt{6}+5}}$ | = | $latex \frac{{4\sqrt{6}-20}}{{-19}}$ |
| $latex \frac{2}{{3+\sqrt{3}}}$ | = | $latex \frac{{3-\sqrt{3}}}{3}$ |
How to rationalize a denominator with a binomial?
Denominators do not always contain a single term, many times we have denominators with binomials. The following are the steps required to rationalize a denominator with a binomial:
Step 1: To rationalize the denominator, we have to multiply both the numerator and the denominator by the conjugate of the denominator. Remember that to find the conjugate, all we have to do is to change the sign that goes between the terms.
Step 2: Perform the multiplication by distributing to both the numerator and denominator.
Step 3: Combine like terms.
Step 4: Simplify the radicals.
Step 5: Combine like terms.
Step 6: Reduce the fraction if possible.
EXAMPLE 1
Rationalize the denominator of the expression $latex \frac{3}{{\sqrt{3}+4}}$.
Step 1: We multiply the numerator and the denominator by the conjugate of the denominator:
$latex \frac{3}{{\sqrt{3}+4}}\times \frac{{\sqrt{3}-4}}{{\sqrt{3}-4}}$
Step 2: We distribute the multiplication:
$latex \frac{{3\sqrt{3}-12}}{{\sqrt{9}+4\sqrt{3}-4\sqrt{3}-16}}$
Step 3: We combine like terms:
$latex \frac{{3\sqrt{3}-12}}{{\sqrt{9}-16}}$
Step 4: We simplify the radicals:
$latex \frac{{3\sqrt{3}-12}}{{3-16}}$
Step 5: We combine like terms:
$latex \frac{{3\sqrt{3}-12}}{{-13}}$
Step 6: The fraction can no longer be simplified.
EXAMPLE 2
Rationalize the denominator of the expression $latex \frac{{3\sqrt{6}+2\sqrt{3}}}{{4\sqrt{6}+3\sqrt{3}}}$.
Step 1: We start by multiplying the numerator and denominator by the conjugate of the denominator:
$$\frac{{3\sqrt{6}+2\sqrt{3}}}{{4\sqrt{6}+3\sqrt{3}}}\times \frac{{4\sqrt{6}-3\sqrt{3}}}{{4\sqrt{6}-3\sqrt{3}}}$$
Step 2: We apply and distribute the multiplication:
$$\frac{{12\sqrt{{36}}+8\sqrt{{18}}-9\sqrt{{18}}-6\sqrt{9}}}{{16\sqrt{{36}}+12\sqrt{{18}}-12\sqrt{{18}}-9\sqrt{9}}}$$
Step 3: We combine like terms:
$latex \frac{{12\sqrt{{36}}-\sqrt{{18}}-6\sqrt{9}}}{{16\sqrt{{36}}-9\sqrt{9}}}$
Step 4: We simplify the radicals:
$latex \frac{{12\left( 6 \right)-3\sqrt{2}-6\left( 3 \right)}}{{16\left( 6 \right)-9\left( 3 \right)}}$
$latex =\frac{{72-3\sqrt{2}-18}}{{96-27}}$
Step 5: We combine like terms:
$latex \frac{{64-3\sqrt{2}}}{{69}}$
Step 6: The fraction can no longer be reduced.
EXAMPLE 3
Rationalize the denominator of the expression $latex \frac{{2\sqrt{8}}}{{3\sqrt{6}-5\sqrt{2}}}$.
Step 1: We start by multiplying the numerator and denominator by the conjugate of the denominator:
$$\frac{{2\sqrt{8}}}{{3\sqrt{6}-5\sqrt{2}}}\times \frac{{3\sqrt{6}+5\sqrt{2}}}{{3\sqrt{6}+5\sqrt{2}}}$$
Step 2: We apply and distribute the multiplication:
$$ \frac{{12\sqrt{{36}}+8\sqrt{{18}}-9\sqrt{{18}}-6\sqrt{9}}}{{16\sqrt{{36}}+12\sqrt{{18}}-12\sqrt{{18}}-9\sqrt{9}}}$$
Step 3: We combine like terms:
$latex \frac{{6\sqrt{{48}}+10\sqrt{{16}}}}{{9\sqrt{{36}}-25\sqrt{4}}}$
Step 4: We simplify the radicals:
$latex \frac{{6\left( {4\sqrt{3}} \right)+10\left( 4 \right)}}{{9\left( 6 \right)-25\left( 2 \right)}}$
$latex =\frac{{24\sqrt{3}+40}}{{54-50}}$
Step 5: We combine like terms:
$latex \frac{{24\sqrt{3}+40}}{4}$
Step 6: We simplify the fraction.
$latex 6\sqrt{3}+10$
Try solving the following practice problems
See also
Interested in learning more about algebraic expressions and factoring? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
