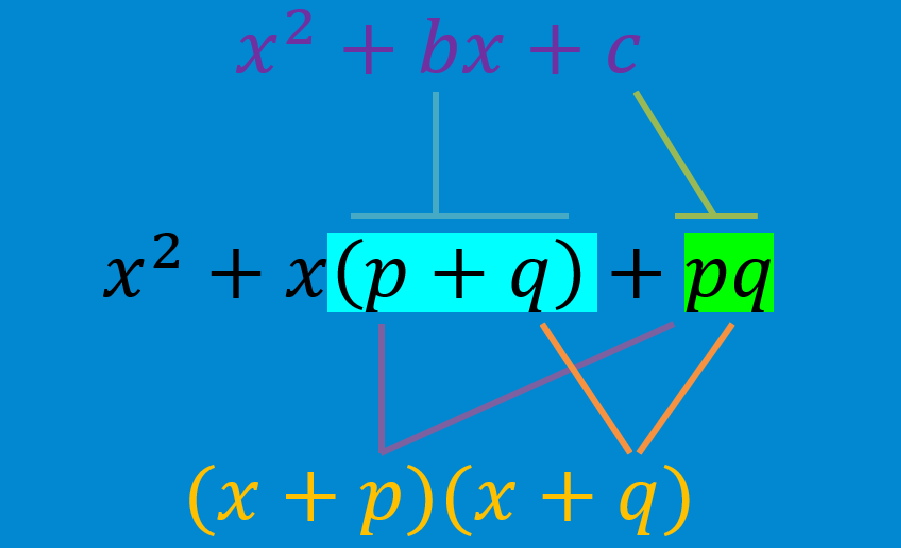Factoring Quadratic Polynomials – Cases and Examples

EXAMPLE 1

Solve the equation $latex 2(x^2+1)=5x$.

Solution: We start by expanding and moving all the terms to the left of the equals sign:

$latex 2(x^2+1)=5x$

⇒  $latex 2x^2+2=5x$

⇒  $latex 2x^2-5x-2=0$

Then, we separate the middle term to factor:

⇒  $latex 2x^2-4x-x-2=0$

⇒  $latex (x-2)(2x-1)=0$

Now, we can set each factor equal to zero and solve:

⇒  $latex (x-2)=0$   y   $latex (2x-1)=0$

⇒  $latex x=2$   y   $latex x=\frac{1}{2}$

EXAMPLE 2

Solve the equation $latex 3x^2-8x-5=0$.

Solution: In this case, we have nothing to expand and all the terms are already on the left, so we start by separating the middle terms and factoring:

$latex 3x^2-8x-5=0$

⇒  $latex 3x(x-3)+1(x-3)=0$

⇒  $latex (3x+1)(x-3)=0$

Now, we can set each factor equal to zero and solve:

⇒  $latex (3x+1)=0$   y   $latex (x-3)=0$

⇒  $latex x=-\frac{1}{3}$   y   $latex x=3$

EXAMPLE 3

Solve the equation $latex (2x-3)^2=25$.

Solution: We start by expanding the equation to obtain:

$latex 4x^2-12x+9-25=0$

⇒  $latex 4{{x}^2}-12x-16=0$

Now, we can divide the entire expression by 4 and factor:

⇒  $latex {{x}^2}-3x-4=0$

⇒  $latex (x-4)(x+1)=0$

Now, we can set each factor equal to zero and solve:

⇒  $latex (x-4)=0$   y   $latex (x+1)=0$

⇒  $latex x=4$   y   $latex x=-1$There are several methods for factoring quadratic polynomials. Our approach here will be to factor quadratic polynomials in which the coefficient of x² is either 1 or greater than 1.

Therefore, we will use trial and error to get the correct factors to factor the quadratic equations.

EXAMPLE 1

Factor and solve the equation $latex {{x}^2}+5x+6=0$.

Solution: We list the factors of 6: 1×6,  2×3.

Now, we identify the factors with a product of 6 and a sum of 5:

1+6≠5

2+3=5

We check the factors using the distributive property:

$$(x+2)(x+3)={{x}^2}+2x+3x+6$$

$latex ={{x}^2}+5x+6$

Therefore, the factored equation is:

$latex (x+2)(x+3)=0$

Now, we can set each factor equal to zero and solve:

⇒  $latex (x+2)=0$   y   $latex (x+3)=0$

⇒  $latex x=-2$   y   $latex x=-3$

EXAMPLE 2

Factor and solve the equation $latex {{x}^2}+8x+16=0$.

Solution: We identify the factors that produce a product of 16 and a sum of 8:

4×4=16   y   4+4=8

We check the factors using the distributive property:

$$(x+4)(x+4)={{x}^2}+4x+4x+16$$

$latex ={{x}^2}+8x+16$

The factored equation is:

$latex (x+4)(x+4)=0$

We set each factor equal to zero and solve:

⇒  $latex (x+4)=0$   y   $latex (x+4)=0$

⇒  $latex x=-4$

EXAMPLE 1

Factor and solve the equation $latex {{x}^2}+4x-5=0$.

Solution: We start by writing the factors of -5:  -1×5,  1×-5.

We identify the factors that produce a product of -5 and a sum of 4:

-1+5=4

1-5≠4

We check the factors using the distributive property:

$$(x-1)(x+5)={{x}^2}-x+5x+-5$$

$latex ={{x}^2}+4x-5$

The factored equation is:

$latex (x-1)(x+5)=0$

We set each factor equal to zero and solve:

⇒  $latex (x-1)=0$   y   $latex (x+5)=0$

⇒  $latex x=1$   y    $latex x=-5$

EXAMPLE 1

Factor and solve the equation $latex {{x}^2}-2x-8=0$.

Solution: We start by writing the factors of -8:  -1×8,  1×-8,  -2×4, 2×-4.

We identify the factors that produce a product of -8 and a sum of -2:

2-4=-2

We check the factors using the distributive property:

$$(x+2)(x-4)={{x}^2}+2x-4x-8$$

$latex ={{x}^2}-2x-8$

The factored equation is:

$latex (x+2)(x-4)=0$

We set each factor equal to zero and solve:

⇒  $latex (x+2)=0$   y   $latex (x-4)=0$

⇒  $latex x=-2$   y    $latex x=4$

EXAMPLE 1

Factor and solve the equation $latex {{x}^2}-7x+10=0$.

Solution: We start by writing the factors of 10:  -1×-10,  -2×-5.

We identify the factors that produce a product of 10 and a sum of -7:

-2-5=-7

-1-10≠-7

We check the factors using the distributive property:

$$(x-2)(x-5)={{x}^2}-2x-5x+10$$

$latex ={{x}^2}-7x+10$

The factored equation is:

$latex (x-2)(x-5)=0$

We set each factor equal to zero and solve:

⇒  $latex (x-2)=0$   y   $latex (x-5)=0$

⇒  $latex x=2$   y    $latex x=5$

EXAMPLE 1

Factor and solve the equation $latex 2{{x}^2}-14x+20=0$.

Solution: In this case, we start by looking for whether we have common factors in the expression. Here, we can extract the 2:

⇒   $latex 2({{x}^2}-7x+10)=0$

Now, we can find the factors of $latex ({{x}^2}-7x+10)$.Therefore, we write the factors of 10: -1×-10 ,  -2×-5.

We identify the factors that produce a sum of -7:

-2-5=-7

-1-10≠-7

We check the factors using the distributive property:

$$2(x-2)(x-5)=2({{x}^2}-2x-5x+10)$$

$latex =2({{x}^2}-7x+10)$

$latex =2{{x}^2}-14x+20$

The factored equation is:

$latex 2(x-2)(x-5)=0$

We set each factor equal to zero and solve:

⇒  $latex (x-2)=0$   y   $latex (x-5)=0$

⇒  $latex x=2$   y    $latex x=5$

EXAMPLE 2

Factor and solve the equation $latex 7{{x}^2}+18x+11=0$.

Solution: We write the factors of 7 and 11:

1×7=7

1×11=11

We apply the distributive property to verify the factors:

$$(7x+1)(x+11)\ne 7{{x}^2}+18x+11$$

$$(7x+11)(x+1)=7{{x}^2}+18x+11$$

The factored equation is:

$latex (7x+11)(x+1)=0$

We set each factor equal to zero and solve:

⇒  $latex (7x+11)=0$   y   $latex (x+1)=0$

⇒  $latex x=-\frac{11}{7}$   y    $latex x=-1$

EXAMPLE 3

Factor and solve the equation $latex 9{{x}^2}+6x+1=0$.

Solution: Following the same process as the previous examples, we can obtain the factored equation:

$latex (3x+1)(3x+1)=0$

We set each factor equal to zero and solve:

⇒  $latex (3x+1)=0$   y   $latex (3x+1)=0$

⇒  $latex x=-\frac{1}{3}$

EXAMPLE 4

Factor and solve the equation $latex 6{{x}^2}-7x+2=0$.

Solution: We can start by separating the middle term:

$latex 6{{x}^2}-4x-3x+2=0$

And now we follow the same process used in the previous examples:

$latex 2x(3x-2)-1(3x-2)=0$

$latex (3x-2)(2x-1)=0$

We set each factor equal to zero and solve:

⇒  $latex (3x-2)=0$   y   $latex (2x-1)=0$

⇒  $latex x=\frac{2}{3}$    y    $latex x=\frac{1}{2}$