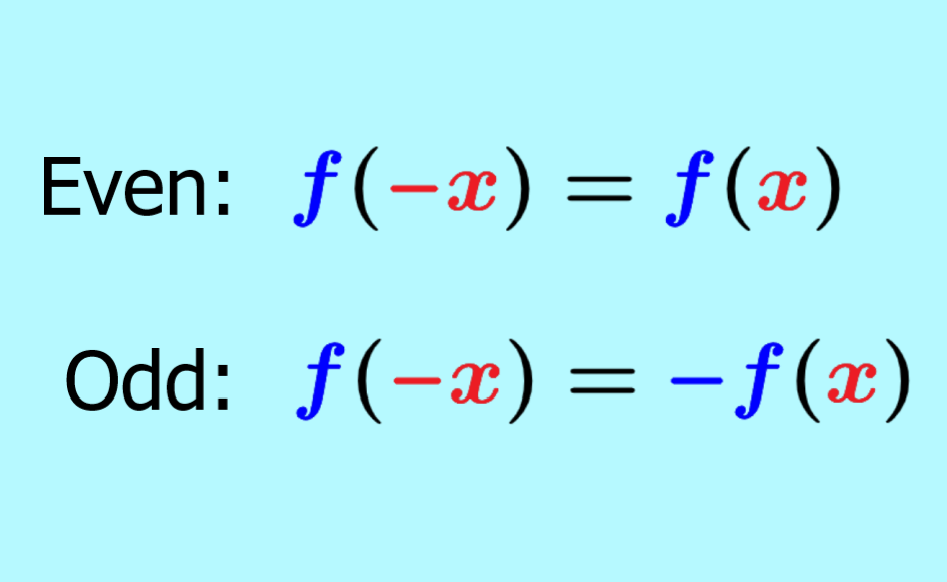An even function is a function, which has a graph with symmetry about the y-axis. On the other hand, the odd function has a graph with rotational symmetry of 180° about the origin. A function is even when f(-x) = f(x) and it is odd when f(-x) = f(x).
Here, we will learn how to determine whether a function is even or odd, both graphically and algebraically. We will look at some examples to practice the concepts.
How to determine if a function is even or odd graphically
Since the graphs of even and odd functions have unique characteristics, we can determine whether a function is even or odd using its graph.
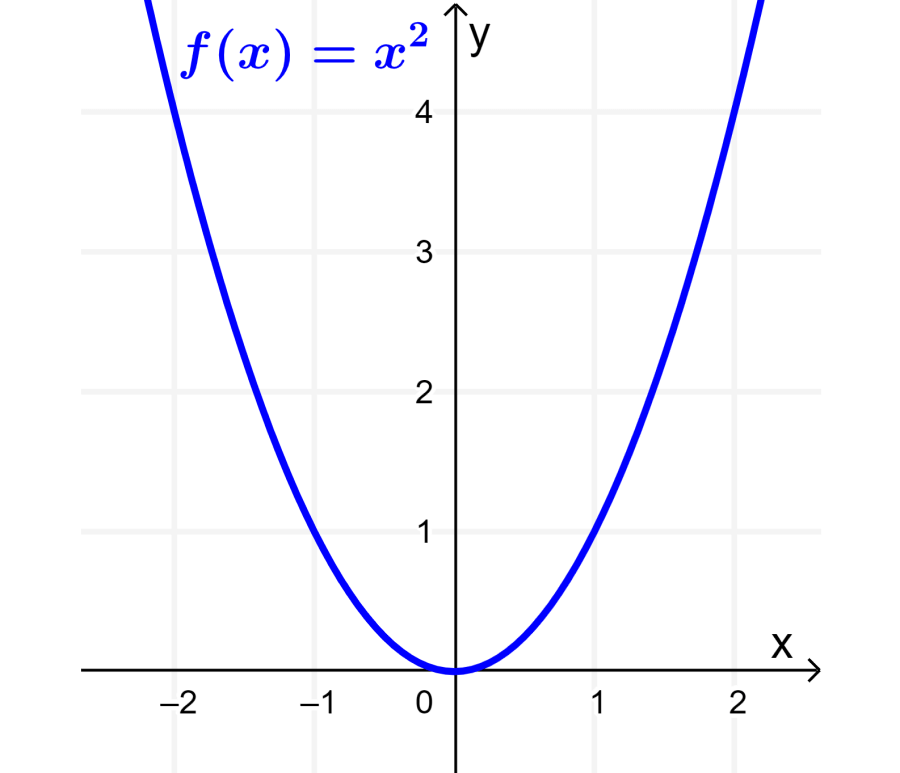
Even Function: The graph of an even function is symmetric about the y-axis. This means that if we were to fold the function on the y-axis, we would get two equal parts of the graph.
For example, the function $latex f(x)=x^2$ is an even function because it has symmetry on the y-axis as shown in the following graph:
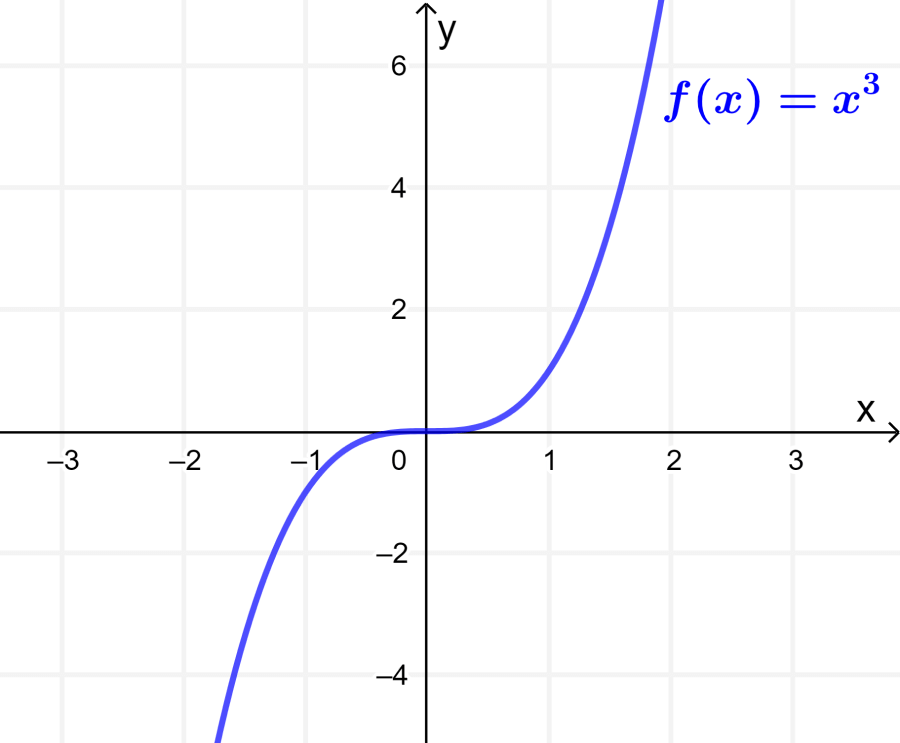
Odd Function: The graph of an odd function has rotational symmetry of 180° about the origin. This means that if we rotate the graph by 180°, the graph remains unchanged.
For example, the function $latex f(x)=x^3$ is an odd function because its graph does not change when we rotate it by 180° about the origin:
How to determine if a function is even or odd algebraically
When we don’t have a graph of the function, we can determine if a function is even or odd algebraically. For this, we consider the following.
Even Function: A function is even if $latex f(-x)=f(x)$ for all values of x that belong to the domain of the function.
For example, the function $latex f(x)=x^2$ is even, since:
$latex f(-x)=(-x)^2=x^2=f(x)$
Odd Function: A function is odd if $latex f(-x)=-f(x)$ for all values of x that belong to the domain of the function.
For example, the function $latex f(x)=x^3$ is odd, since:
$latex f(-x)=(-x)^3=-x^3=-f(x)$
In short, if we have a function f such that $latex f(-x)=f(x)$, the function is even. If we have a function f such that $latex f(-x)=-f(x)$, the function is odd
Determining if a function is even or odd – Examples with answers
Graphical and algebraic methods are used to solve the following odd and even function examples. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Prove that the function $latex f(x)=x^2-2$ is even.
Solution
The graph of the function $latex f(x)=x^2-2$ is equal to the graph of $latex f(x)=x^2$ translated 2 units down:
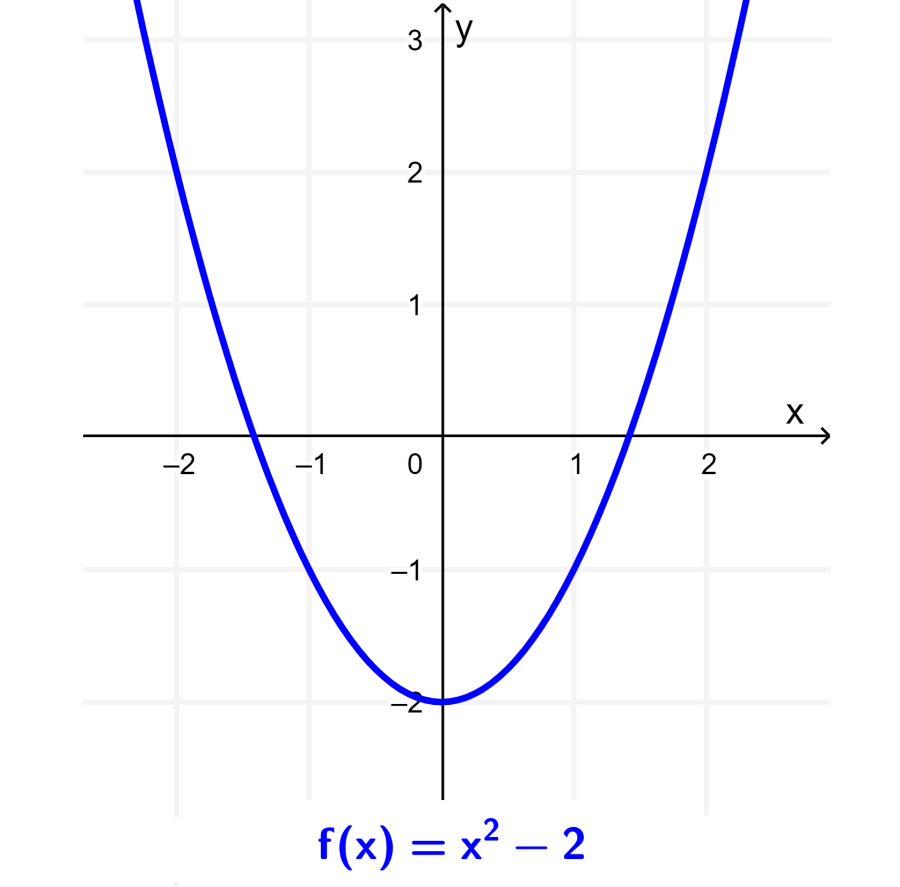
Clearly, we see that the graph of $latex f(x)=x^2-2$ is symmetric about the y-axis. This means that the function is even.
EXAMPLE 2
Prove that the function $latex f(x)=2x^4+x^2-1$ is an even function.
Solution
Proving this graphically would be more difficult. Therefore, let’s prove algebraically.
If the function is even, we must have $latex f(-x)=f(x)$. Thus, we check:
$latex f(-x)=2(-x)^2+(-x)^2-1$
$latex f(-x)=2x^2+x^2-1$
We see that we got the original function, so we have proved that the function is even.
EXAMPLE 3
Prove that the function $latex f(x)=4x^3-x$ is an odd function.
Solution
Odd functions are generally difficult to demonstrate graphically. Therefore, let’s prove algebraically.
If a function is odd, we must have $latex f(-x)=-f(x)$. Then, we check this:
$latex f(-x)=4(-x)^3-(-x)$
$latex f(-x)=-4-x^3+x$
The expression on the right-hand side is equivalent to having $latex -f(x)$. This means that the function is odd.
EXAMPLE 4
Determine whether the function $latex f(x)=3x^2-|x|$ is odd or even.
Solution
To prove whether a function is even or odd, we can start by performing the even function test. If the function fails that test, we can proceed with the odd function test.
For a function to be even, we must have $latex f(-x)=f(x)$. Checking, we have:
$latex f(-x)=3(-x)^2-|-x|$
$latex f(-x)=3x^2-|x|$
We see that the expression we got is equal to $latex f(x)$, so the function is even.
Since the function is even, we no longer have to test for odd functions.
EXAMPLE 5
Determine whether the function $latex f(x)=\frac{1}{x}+x$ is odd or even.
Solution
Again, we can start with the even functions test and then carry out the test for odd functions.
For a function to be even, we must have $latex f(-x)=f(x)$. Checking, we have:
$latex f(-x)=\frac{1}{-x}+(-x)$
$latex f(-x)=-\frac{1}{x}-x$
We see that the expression we got is not equal to $latex f(x)$, so the function is not even. Thus, we proceed with the test for odd functions.
For a function to be odd, we must have $latex f(-x)=-f(x)$. Looking at the expression we got above, we see that the resulting expression is indeed equal to $latex -f(x)$, so the function is odd.
EXAMPLE 6
Determine whether the function $latex f(x)=(x^3-5)^2$ is even, odd, or neither.
Solution
We start with the test for even functions. Therefore, we check if $latex f(-x)=f(x)$:
$latex f(-x)=((-x)^3-5)^2$
$latex f(-x)=(-x^3-5)^2$
The expression we got is not equal to $latex f(x)$. Thus, we proceed with the test for odd functions.
To check if the function is odd, we must have $latex f(-x)=-f(x)$. However, the function is also not odd, since the expression obtained above is not equal to $latex -f(x)$.
Note: $latex -f(x)$ would be equal to $latex -(x^3-5)^2$.
Determining if a function is even or odd – Practice problems
Use the odd and even function tests to solve the following practice problems. You can use the examples with answers shown above as a guide.
See also
Interested in learning more about algebraic functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
