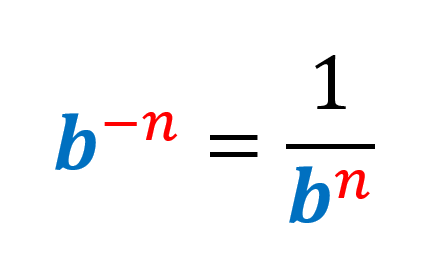The negative exponents’ problems can be solved by applying the negative exponents’ rule, which tells us that a negative exponent can be transformed into a positive one by taking the reciprocal of its base.
Here, we will look at a summary of expressions with negative exponents. Then, we will see several examples with answers to learn how to solve these types of problems. We will also look at interactive problems to put what we have learned into practice.
Summary of negative exponents
The negative exponent in an expression tells us to rewrite this expression by taking the reciprocal of the base and then changing the sign of the exponent.
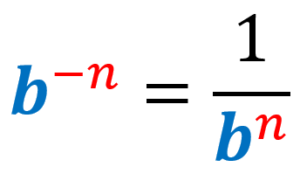
Any expression that has negative exponents is not considered an expression in its simplest form. We simply flip the fraction and convert the negative exponent to a positive exponent.
Negative exponents – Examples with answers
The following negative exponent examples have their respective solution to learn the process and the reasoning behind each answer. It is recommended that you try to solve the exercises yourself before looking at the solution.
EXAMPLE 1
Simplify the expression $latex {{5}^{-1}}$.
Solution
The negative exponent rule tells us that $latex {{b}^{-n}}=\frac{1}{{{b}^n}}$. Therefore, we have to take the reciprocal of the base and change the exponent from negative to positive:
$latex {{5}^{-1}}=\frac{1}{{{5}^1}}$
Now, we apply the exponent to simplify:
$latex \frac{1}{{{5}^1}}=\frac{1}{5}$
EXAMPLE 2
Simplify the expression $latex 3^{-3}$.
Solution
Using the negative exponents rule $latex {{b}^{-n}}=\frac{1}{{{b}^n}}$, we take the reciprocal of 3 and change the exponent to positive:
$latex {{3}^{-3}}=\frac{1}{{{3}^3}}$
We simplify by applying the exponent:
$latex \frac{1}{{{3}^3}}=\frac{1}{27}$
EXAMPLE 3
Simplify the algebraic expression $latex 2{{x}^{-4}}$.
Solution
In this case, only the variable is raised to a negative exponent, so the negative exponents’ rule only applies to the variable. We take the reciprocal of x and -4 changes to 4:
$latex 2{{x}^{-4}}=\frac{2}{{{x}^4}}$
In this case, we no longer have anything to simplify.
EXAMPLE 4
Simplify the algebraic expression $latex {{3}^{-2}}{{x}^{-3}}$.
Solution
We take the reciprocal of 3 and raise it to positive 2 and we take the reciprocal of x and raise it to positive 3:
$latex {{3}^{-2}} {{x}^{-3}}=\frac{1}{{{3}^2}{{x}^3}}$
We apply the exponent of 3 to simplify:
$latex \frac{1}{{{3}^2}{{x}^3}}=\frac{1}{9{{x}^3}}$
EXAMPLE 5
Simplify the algebraic expression $latex \frac{4x}{{{2}^{-2}}}$.
Solution
Here, we start with a fraction and a negative exponent in the denominator. Therefore, we apply the negative exponents’ rule to the denominator:
$latex \frac{4x}{{{2}^{-2}}}=4x({{2}^2})$
We simplify by applying the exponent:
$latex 4x({{2}^2})=4x(4)$
$latex =16x$
EXAMPLE 6
Simplify the algebraic expression $latex \frac{{{x}^{-2}}}{5({{5}^{-3}})}$.
Solution
We have negative exponents in both the numerator and the denominator. We take the reciprocal of x and raise it to the positive power of 2. We take the reciprocal of 5 and raise it to the positive power of 3 :
$latex \frac{{{x}^{-2}}}{5({{5}^{-3}})}=\frac{{{5}^3}}{5{{x}^2}}$
We apply the exponent and simplify the fraction:
$latex \frac{{{5}^3}}{5{{x}^2}}=\frac{125}{5{{x}^2}}$
$latex =\frac{25}{{{x}^2}}$
EXAMPLE 7
Simplify the algebraic expression $latex \frac{{{4}^{-2}}{{x}^{-5}}}{{{2}^{-5}}{{x}^{-3}}}$.
Solution
We have negative exponents in both the numerator and the denominator. We take the reciprocal of x and raise it to the positive power of 2. We take the reciprocal of 5 and raise it to the positive power of 3:
$latex \frac{{{4}^{-2}}{{x}^{-5}}}{{{2}^{-5}}{{x}^{-3}}}=\frac{{{2}^5}{{x}^3}}{{{4}^2}{{x}^5}}$
We apply the exponents and simplify the fraction:
$latex \frac{{{2}^5}{{x}^3}}{{{4}^2}{{x}^5}}=\frac{32{{x}^3}}{16{{x}^5}}$
$latex =\frac{2}{{{x}^2}}$
EXAMPLE 8
Simplify the algebraic expression $latex \frac{{{6}^{-3}}{{y}^{-2}}}{{{3}^{-4}}{{y}^{-6}}}$.
Solution
We apply the rule of negative exponents to all variables and numbers. We change the 6 to the y denominator and raise them to the power of 3 positive and 2 positive respectively.
In the same way, we change the 3 and y to the numerator and raise them to the power of 4 positive and 6 positive respectively:
$latex \frac{{{6}^{-3}}{{y}^{-2}}}{{{3}^{-4}}{{y}^{-6}}}=\frac{{{3}^4}{{y}^6}}{{{6}^3}{{y}^2}}$
We simplify everything by applying the exponents:
$latex \frac{{{3}^4}{{y}^6}}{{{6}^3}{{y}^2}}=\frac{81{{y}^6}}{216{{y}^2}}$
$latex =\frac{3{{y}^4}}{8}$
Negative exponents – Practice problems
Test what you have learned with the following negative exponent exercises. Solve the problems and choose your answer. Check your answer by clicking “Check.” See the solved examples above if you have any problems solving these problems.
See also
Interested in learning more about exponents? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
