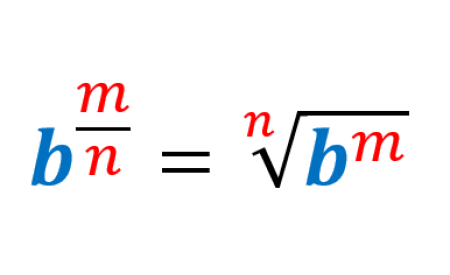Fractional Exponents – Examples and Practice Problems

The fractional exponent rule tells us that $latex {{b}^{\frac{m}{n}}}=\sqrt[n]{{{b}^m}}$. Therefore, we write 3 to the power of 3 and then we take the square root of this:

$latex 3^{\frac{3}{2}}=\sqrt[2]{3^3}$

Now, we simplify the expression by applying the exponent of 3:

$latex \sqrt[2]{3^3}=\sqrt[2]{81}$

We can simplify again by recognizing that the square root of 81 is 9:

$latex \sqrt[2]{81}=9$

Now, we have to write 4 raised to the power of 2 and we have to take the cube root of that expression:

$latex 4^{\frac{2}{3}}=\sqrt[3]{4^2}$

We simplify by applying the exponent:

$latex \sqrt[3]{4^2}=\sqrt[3]{16}$

We can simplify by rewriting 16 as 8 × 2:

$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$

The cube root of 8 is 2, so we have:

$latex \sqrt[3]{8\times 2}=2\sqrt[3]{2}$

Here we have a number and a variable. Raise -2 to the fourth power and take its cube root and square x and take its cube root:

$latex -2^{\frac{4}{3}}x^{\frac{2}{3}}=\sqrt[3]{(-2)^4}\sqrt[3]{x^2}$

We can apply the exponent to -2 to simplify:

$latex \sqrt[3]{(-2)^4}\sqrt[3]{x^2}=\sqrt[3]{16}\sqrt[3]{x^2}$

Similar to the previous problem, we can simplify by rewriting 16 as 8 × 2:

$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$

$latex =2\sqrt[3]{2}$

Therefore, we have:

$latex \sqrt[3]{16}\sqrt[3]{x^2}=2\sqrt[3]{2}\sqrt[3]{x^2}$

Now, we can combine the cube roots to simplify:

$latex 2\sqrt[3]{2}\sqrt[3]{x^2}=2\sqrt[3]{2x^2}$

We write 6 cubed and take its square root. We write to the x raised to the fifth and take its square root:

$latex 6^{\frac{3}{2}}x^{\frac{5}{2}}=\sqrt{6^3}\sqrt{x^5}$

We simplify 6 cubed:

$latex \sqrt{6^3}\sqrt{x^5}=\sqrt{216}\sqrt{x^5}$

It is possible to simplify by writing to 216 as 36 × 6:

$latex \sqrt{216}=\sqrt{36\times 6}$

$latex =6\sqrt{6}$

Therefore, we have:

$latex \sqrt{216}\sqrt{x^5}=6\sqrt{6}\sqrt{x^5}$

Combining the square roots, we have:

$latex 6\sqrt{6}\sqrt{x^5}=6\sqrt{6x^5}$

In this case, we have a negative exponent. Remember that a negative exponent can be transformed to positive by taking the reciprocal of the base. Therefore, we have:

$latex {{4}^{-\frac{3}{2}}}{{x}^{\frac{1}{2}}}=\frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}$

Now, we cube 4 and take its square root and take the square root of the x:

$latex \frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}=\frac{\sqrt{x}}{\sqrt{{{4}^3}}}$

We can apply the exponent to 4 to simplify:

$latex \frac{\sqrt{x}}{\sqrt{{{4}^3}}}=\frac{\sqrt{x}}{\sqrt{64}}$

Now, we can take the square root of 64:

$latex \frac{\sqrt{x}}{\sqrt{64}}=\frac{\sqrt{x}}{8}$

We start transforming the exponent to positive by taking the reciprocal of the base. Therefore, we have:

$latex {{12}^{-\frac{2}{3}}}{{x}^{\frac{3}{5}}}=\frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}$

Now, we square 12 and take its cube root. We cube x and take its fifth root:

$latex \frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}$

We apply the exponent to 12:

$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}$

We can write 144 as 8×18 and take the cube root of 8:

$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{8\times 18}}$

$latex =\frac{\sqrt[5]{{{x}^3}}}{2\sqrt[3]{18}}$

We simply apply the rule of fractional exponents to form radicals:

$latex {{x}^{{\frac{1}{2}}}}{{y}^{{\frac{2}{3}}}}=\sqrt{x}~\sqrt[3]{{{{y}^{2}}}}$

Again, we just have to apply the rule of fractional exponents to form radicals and then we simplify:

$latex {{81}^{{\frac{1}{4}}}}{{x}^{{\frac{3}{2}}}}=\sqrt[4]{{81}}~\sqrt{{{{x}^{3}}}}$

$latex =3~\sqrt{{{{x}^{3}}}}$

Here, we have negative exponents, so we start by transforming negative exponents to positive using the negative exponents rule:

$latex {{4}^{{-\frac{1}{2}}}}{{x}^{{-\frac{1}{2}}}}=\frac{1}{{{{4}^{{\frac{1}{2}}}}{{x}^{{\frac{1}{2}}}}}}$

Now, we use the fractional exponent rule and simplify:

$latex =\frac{1}{{\sqrt{4}~\sqrt{x}}}$

$latex =\frac{1}{{2~\sqrt{x}}}$

We have negative exponents, so we start with the negative exponents rule:

$$\frac{{{{{16}}^{{-\frac{1}{2}}}}~{{y}^{{-\frac{1}{3}}}}}}{{{{x}^{{-\frac{1}{2}}}}~}}=\frac{{{{x}^{{\frac{1}{2}}}}~}}{{{{{16}}^{{\frac{1}{2}}}}~{{y}^{{\frac{1}{3}}}}~}}$$

Now, we use the fractional exponent rule and simplify:

$latex =\frac{{\sqrt{x}}}{{\sqrt{{16}}~\sqrt[3]{y}}}$

$latex =\frac{{\sqrt{x}}}{{4~\sqrt[3]{y}}}$