The exponential function is one of the most important functions in mathematics. To form an exponential function, we make the independent variable the exponent. These functions are used in many real-life situations. They are mainly used for population growth, compound interest, or radioactivity.
Here, we will see a summary of the exponential functions. Also, we will explore various examples of exponential functions problems with answers to understand the use of these functions.
Summary of exponential functions
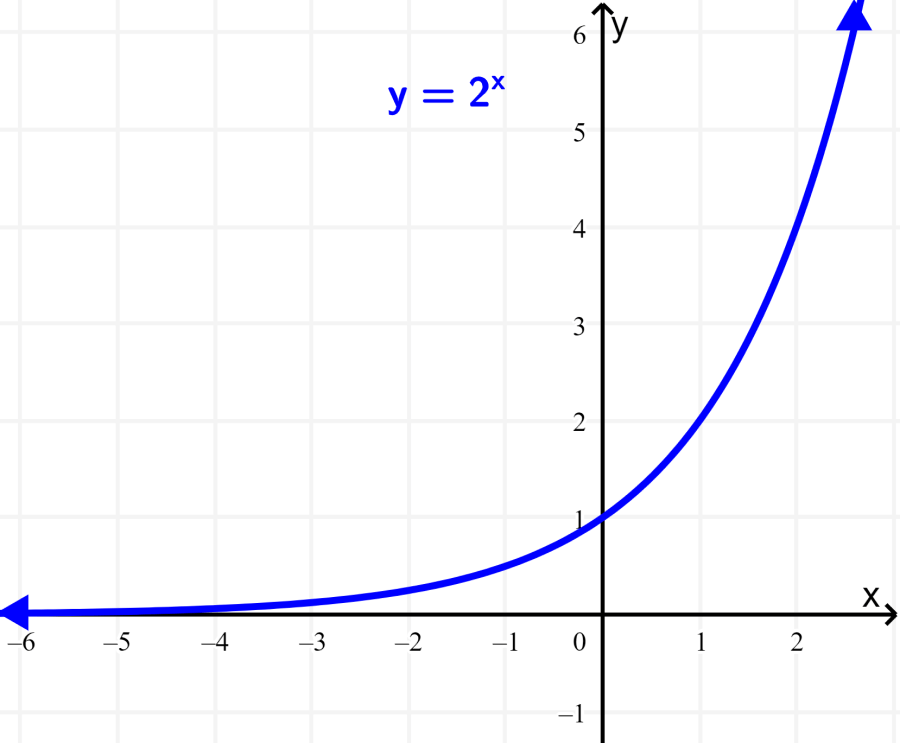
An exponential function is a mathematical function that has the general form $latex f(x)={{b}^x}$, where x is a variable and b is a constant called the base of the function and must be greater than 0. In the exponential functions, the input variable, x, occurs as an exponent.
The following are the properties of the standard exponential function $latex f(x)={{b}^x}$:
1. The graph of $latex f(x)$ will always contain the point (0, 1). This is equivalent to having $latex f(0)=1$ regardless of the value of b.
2. For any possible value of b, we have $latex {{b}^x}>0$. This implies that $latex {{b}^x}$ is different from zero.
3. If we have $latex 0<b<1$, then the graph of $latex f(x)={{b}^x}$ will grow from left to right.
5. If we have $latex {{b}^x}={{b}^y}$, this means that $latex x=y$.
Examples with answers of exponential function problems
The following examples use some of the applications of exponential functions. Each example has its respective solution that can be useful to understand the process and reasoning used.
EXAMPLE 1
Given the function $latex f(x)={{2}^x}$, find $latex f(-2)$.
Solution
To evaluate any function, we simply have to use the given input. Therefore, we have:
$latex f(-2)={{2}^{-2}}$
$latex =\frac{1}{{{2}^2}}$
$latex =\frac{1}{4}$
EXAMPLE 2
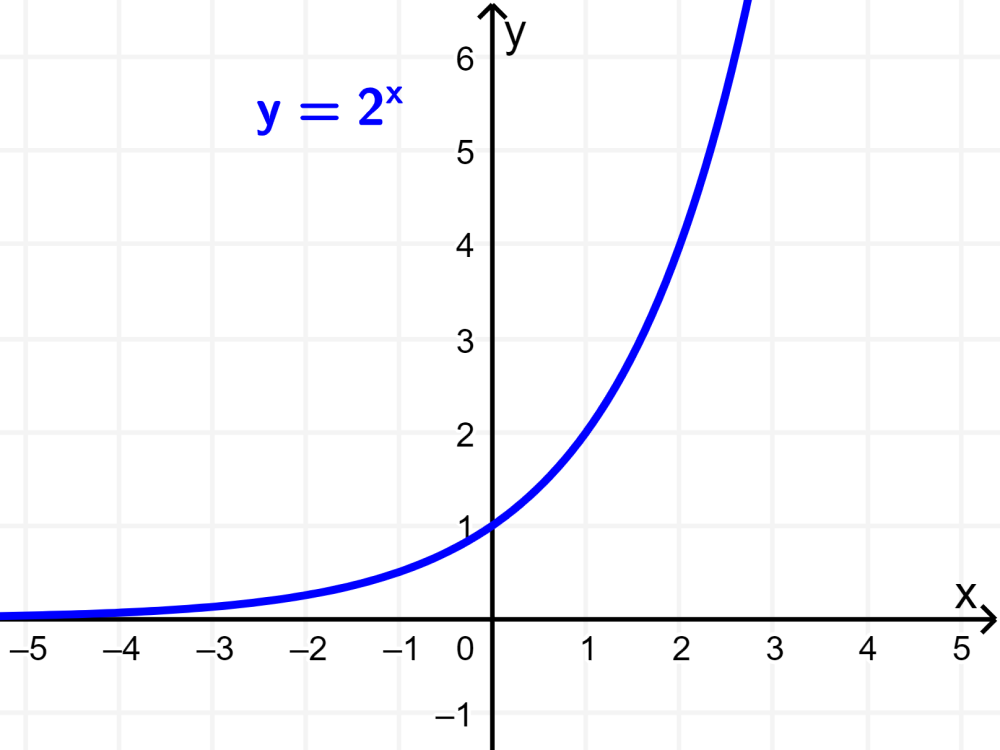
Graph the function $latex f(x)={{2}^x}$.
Solution
To graph a function, we can use various values of x to find points that lie on the graph. We know that all exponential functions pass through the point (0, 1), so we already have a point.
Additionally, we can use the values $latex x=-1$, $latex x=-2$, $latex x=1$ and $latex x=2$:
- When $latex x=-1$, we have $latex f(-1)={{2}^{- 1}} =\frac{1}{2}$.
- When $latex x=-2$, we have $latex f(-2)={{2}^{- 2}} = \frac{1}{4}$.
- When $latex x=1$, we have $latex f(1)={{2}^1}=2$.
- When $latex x=2$, we have $latex f(2)={{2}^2}=4$.
Plotting these points and graphing the curve, we have the following:
EXAMPLE 3
The population of a certain region can be modeled with the formula $latex A=10000({{e}^{0.005t}})$, where A represents the population and t represents time in years. Find the population at the end of 10 years.
Solution
This is an example of using exponential functions to model population growth. We have the function $latex A=10000({{e}^{0.005t}})$ and we have the time $latex t=10$. Substituting $latex t=10$, we have:
$latex A=10000({{e}^{0.005(10)}})$
$latex =10000({{e}^{0.05}})$
$latex =10000(1.0513)$
$latex =10513$
Therefore, the population of the region after 10 years will be 10,513.
EXAMPLE 4
In 1950, the population of a city was 10,000. Twenty years later, the population was found to be 20,000. Find the exponential function that models the population P after t years have passed.
Solution
We know that the exponential function that models population growth has the general form $latex P=N({{e}^{\lambda t}})$, where N is the initial population, λ is a constant and t is time. We have to find the constant λ with the given information. Therefore, we have:
$latex P=N({{e}^{\lambda t}})$
$latex 20000=10000({{e}^{20 \lambda}})$
$latex \frac{20000}{10000}={{e}^{20 \lambda}}$
$latex 2={{e}^{20 \lambda}}$
$latex \ln(2)=20 \lambda$
$latex \frac{\ln(2)}{20}=\lambda$
$latex 0.0347=\lambda$
The formula that models this population growth is $latex P=10000 ({{e}^{0.0347 t}})$.
EXAMPLE 5
Having the population growth formula $latex P=N({{e}^{0.1234t}})$, estimate when the population will reach 37,500 if in 1950 the population was 12,500.
Solution
With the given information, we can complete the population growth formula:
$latex P=N({{e}^{0.1234t}})$
$latex 37500=12500({{e}^{0.1234t}})$
Now, we solve for time:
$latex 37500=12500({{e}^{0.1234t}})$
$latex \frac{37500}{12500}=({{e}^{0.1234t}})$
$latex 3=({{e}^{0.1234t}})$
$latex \ln(3)=0.1234t$
$latex \frac{\ln(3)}{0.1234}=t$
$latex 8.9=t$
This means that the population will reach 37,500 in 1959.
EXAMPLE 6
An amount of USD 10 000 is deposited into an account that pays 7.5% interest compounded four times a year. How much money will there be in the account after 10 years?
Solution
The exponential function used to calculate money with compound interest is $latex D=A{{(1+\frac{r}{n})}^{nt}}$, where, D is the final amount of money, A is the initial amount of money, r is the interest rate in decimals, n is the number of times the interest is compounded per year, and t is the time in years.
Using the given data, we have:
$latex D=10000{{(1+\frac{0.075}{4})}^{4(10)}}$
$latex D=10000{{(1.01875)}^{40}}$
$latex D=21023.5$
Therefore, after 10 years, there will be USD 21023.5 in the account.
EXAMPLE 7
If we have USD 2 000 in an account that pays 7% compound interest four times a year, how long will it take for the account to have USD 10,000?
Solution
We can use the given data to form the exponential function of compound interest:
$latex D=A{{(1+\frac{r}{n})}^{nt}}$
$latex 10000=2000{{(1+\frac{0.07}{4})}^{4t}}$
$latex 10000=2000{{(1.0175)}^{4t}}$
$latex \frac{10000}{2000}={{(1.0175)}^{4t}}$
$latex 5={{(1.0175)}^{4t}}$
$latex \ln(5)=\ln({{(1.0175)}^{4t}})$
$latex \ln(5)=4t\ln(1.0175)$
$latex \frac{\ln(5)}{\ln(1.0175)}=4t$
$latex \frac{99.77}{4}=t$
$latex 23.2=t$
Therefore, after 23.2 years, there will be USD 10 000 in the account.
→ Exponential Equations Calculator
Exponential function problems – Practice problems
Test your knowledge of exponential functions with the following problems. Solve the exercises and select your answer. Check your chosen answer to see if it is correct. See the solved examples above if you need help.
See also
Interested in learning more about exponential functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
