The sine of an angle is a function that relates to the sides of a right triangle. Specifically, the sine is found by taking the side that is opposite the angle and dividing it by the hypotenuse of the triangle. Outside the triangle, the sine function can be used to find the y component of a vector that has any angle. The sine is also equivalent to the cosine of the complementary angle.
Here, we will learn more details about the sine of angles. We will know the learn about the sine of important angles and we will solve some practice problems.
Definition of the sine of an angle
The sine of an angle is defined using a right triangle. When we have a right triangle, the sine is equal to the length of the side opposite the angle divided by the length of the hypotenuse of the triangle.
On the other hand, the sine can also be defined as the cosine of the complementary angle. In turn, the complementary angle is defined as 90° (a right angle) minus the given angle. For example, the complement of the angle 30° is equal to 90°-30° = 60°.
Therefore, for an angle θ, we have the following relationship:
$latex \sin(\theta)=\cos(90^{\circ}-\theta)$
In terms of radians, we have:
$latex \sin(\theta)=\cos(\frac{\pi}{2}-\theta)$
Sines in right triangles
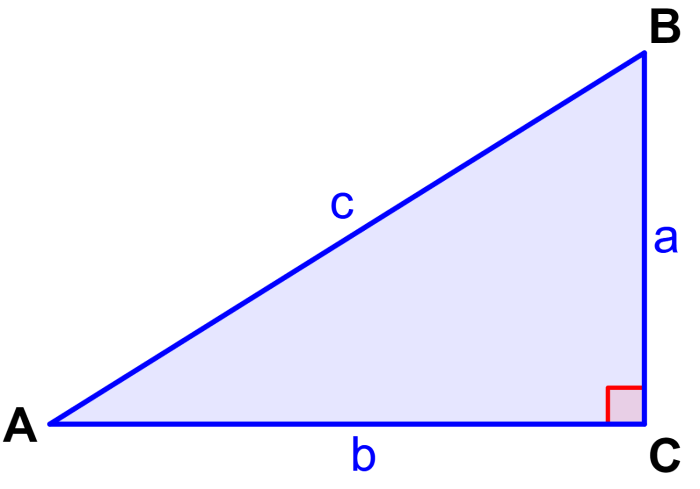
We can define the sine function using the following right triangle that has a right angle at C.
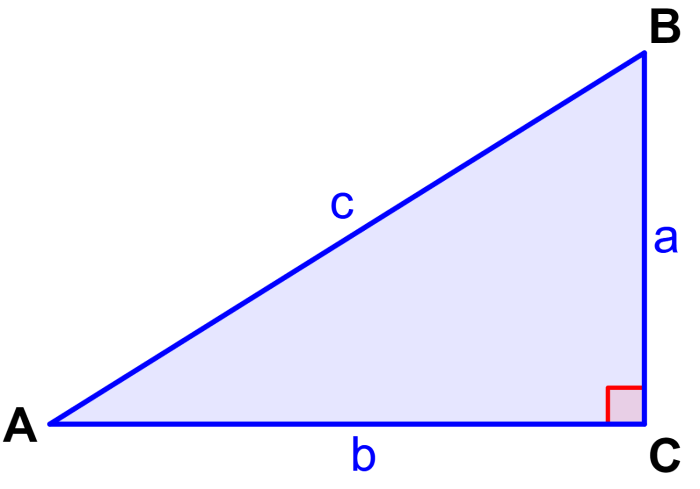
Generally, we use lowercase letters to denote the sides of triangles and capital letters to denote the respective angles. For example, side a is the side opposite angle A, side b is the side opposite angle B, and side c is the side opposite angle C.
All triangles have interior angles that add up to 180°. We know that angle C measures 90°, so we know that angles A and B must add up to 90° (complementary angles).
Therefore, we can deduce that the sine of angle A is equal to the cosine of angle B. The sine of an angle in a right triangle is equal to the opposite side divided by the hypotenuse:
| $latex \sin=\frac{\text{opposite}}{\text{hypotenuse}}$ |
Using this, we have the relations $latex \sin(A)=\frac{a}{c}$ y $latex \sin(B)=\frac{b}{c}$ in the triangle above.
Sines for common special angles
The values of the sines of the most important angles can be found using the proportions of the special triangles. To find the value of the sine of 45° we use a right isosceles triangle, which has the angles 45°-45°-90°.
In a right triangle, we can use the Pythagorean theorem: $latex {{c}^2} = {{a}^2}+{{b}^2}$. However, in the case of the 45°-45°-90° triangle, we have $latex a = b$, so the Pythagorean theorem becomes $latex {{c}^2}=2{{a}^2}$.
Solving, we have $latex c= a \sqrt{2}$. Using this, we determine that both the sine and cosine of 45° are equal to $latex \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
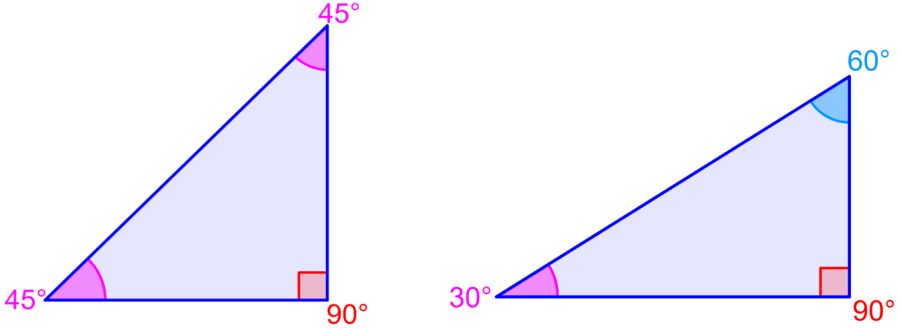
We can also use the 30°-60°-90° triangle to find the sine values of 30° and 60°. The proportions of the sides of this triangle are 1:$latex \sqrt{3}$:2. Using these proportions, we have $latex \sin(30^{\circ})=\cos(60^{\circ})=\frac{1}{2}$ and we also have $latex \sin(60^{\circ})=\cos(30^{\circ})=\frac{\sqrt{3}}{2}$.
| Degrees | Radians | Sine |
| 90° | $latex \frac{\pi}{2}$ | 1 |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{\sqrt{3}}{2}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ |
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{1}{2}$ |
| 0° | 0 | 0 |
Sine of an angle – Examples with answers
The following examples are solved using what has been learned about the sine of an angle. Each example has its respective solution, but it is recommended that you try to solve the problems yourself before looking at the solution.
EXAMPLE 1
If we have $latex \cos(A) = 0.25$ and $latex a=5$, what is the value of c?
Solution
We use the right triangle above to get the correct relationships. Therefore, we can use the equation $latex \sin(A) = \frac{a}{c}$. Using this equation with the given values and solving for c, we have:
$latex \cos(A)=\frac{a}{c}$
$latex 0.25=\frac{5}{c}$
$latex c=\frac{5}{0.25}$
$latex c=20$
The value of the hypotenuse is 20.
EXAMPLE 2
We have $latex b=8$ and $latex \sin(B) = \frac{1}{4}$. What is the value of c?
Solution
If we use the right triangle above, we have the equation $latex \cos(B) = \frac{b}{c}$. Therefore, we use this equation along with the given values and solve for c:
$latex \cos(B)=\frac{b}{c}$
$latex \frac{1}{4}=\frac{8}{c}$
$latex c=4(8)$
$latex c=32$
The value of the hypotenuse is 32.
EXAMPLE 3
What is the value of B if we have $latex b = 5$ and $latex c = 9$?
Solution
Using this relation: $latex \sin(B)=\frac{b}{c}$. Substituting the given values, we have:
$latex \sin(B)=\frac{b}{c}$
$latex \sin(B)=\frac{5}{9}$
$latex \sin(A)=0.556$
We use the function $latex {{\sin}^{-1}}$ on a calculator to get the result:
$latex {{\sin(0.556)}^{-1}}=33.8$°
Angle B measures 33.8°.
→ Sine Calculator (Degrees and Radians)
Sine of an angle – Practice problems
Use what you have learned about the sine of an angle to solve the following practice problems. Select an answer and check it to see if you got the correct answer.
See also
Interested in learning more about sine of an angle? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
