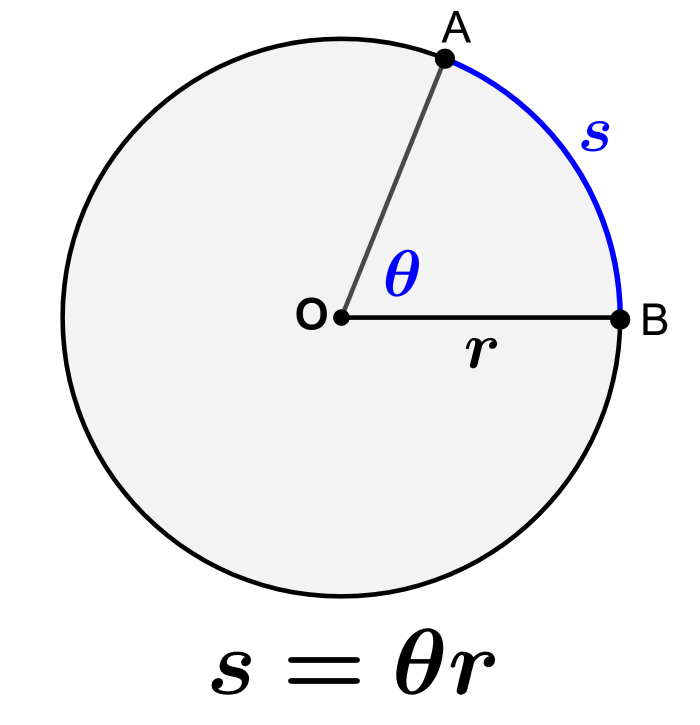
An arc of a circumference or of a circle is a portion of the circumference. The length of an arc is simply the length of this portion of the circumference. The circumference itself can be considered an arc that goes around the circle.
Here, we will learn about the different formulas and methods that we can use to find the arc length using both degrees and radians. Then, we will look at some exercises where we will apply these methods.
How to find the arc length?
The length of the arc is equal to the length of a portion of the circumference. In addition, we also have to consider the measure of the arc, which is equal to the central angle that intersects the arc. We can look at the measurement of the arc and the length of the arc in the following diagram:
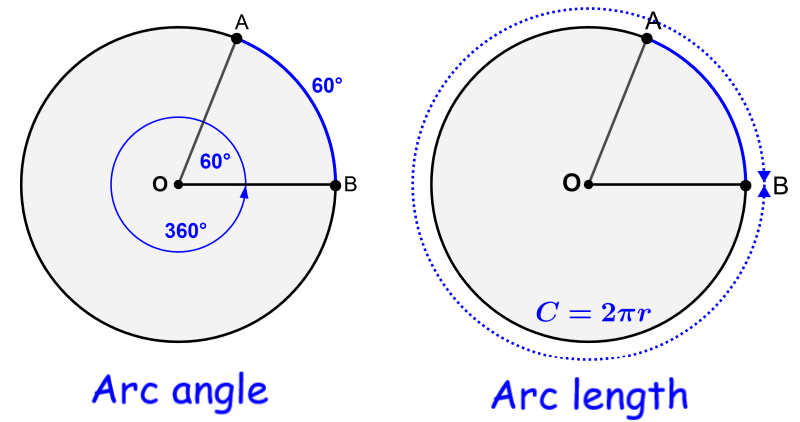
Now, let’s consider the following proportions:
$latex \frac{\text{arc angle}}{360^{\circ} }=\frac{\text{arc length}}{\text{circumference}}$
We can solve this for the arc length and replace “arc angle” with “central angle” since they are equivalent. Therefore, we have:
$$\text{arc length}=\frac{\text{central angle}}{360^{\circ}}\times \text{circumference}$$
We can see that the length of the arc is a fractional part of the circumference. For example, the arc measure of 60° is equal to one-sixth of 360°, which means that the length of the arc will also be equal to one-sixth of the length of the circumference.
Arc angles in radians
The radian measure, θ, of a central angle is defined as the ratio of the length of the arc, s, divided by the radius of the circle, r:
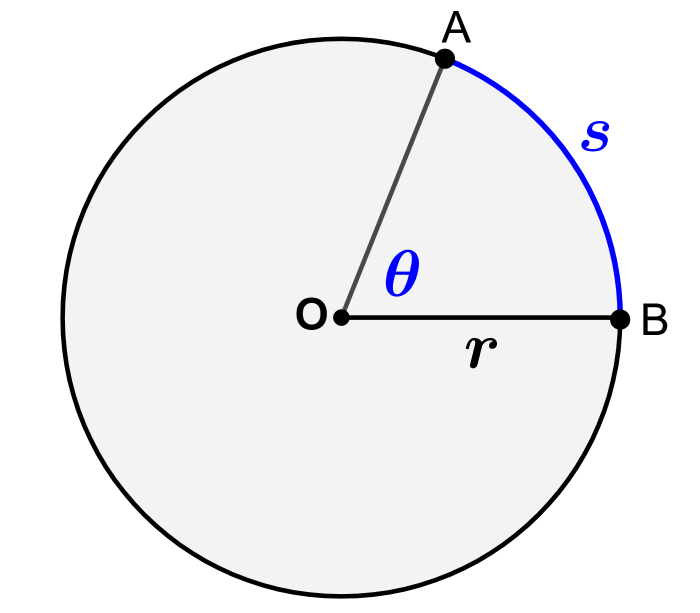
Using this, we can calculate the length of the arc as follows:
$latex s= \theta r$
Arc of a circumference – Examples with answers
The formulas and methods listed above are used to find the lengths of the arcs in the following examples. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the length of an arc that has a central angle of 60° if the circumference is 12 m?
Solution
The value of the central angle is 60° and the length of the circumference is 12 m. Therefore, we substitute these values in the arc length formula:
$$\text{arc length}=\frac{\text{central angle}}{360^{\circ}}\times \text{circumference}$$
$latex =\frac{60^{\circ}}{360^{\circ}}\times 12$
$latex =\frac{1}{6}\times 12$
$latex =2$
The length of the arc is equal to 2 m.
EXAMPLE 2
If an arc has a central angle of 40° and the circumference has a length of 27 m, what is the length of the arc?
Solution
The central angle is 40° and the circumference is 27 m. Using these values in the arc length formula, we have:
$$\text{arc length}=\frac{\text{central angle}}{360^{\circ}}\times \text{circumference}$$
$latex =\frac{40^{\circ}}{360^{\circ}}\times 27$
$latex =\frac{1}{9}\times 27$
$latex =3$
The length of the arc is equal to 3 m.
EXAMPLE 3
What is the length of an arc that has a central angle of 120° and is formed by a radius of 6 m?
Solution
In this case, we have the value of the radius instead of the circumference. Therefore, we have to calculate the length of the circumference using the radius $latex r=6$. Therefore, we have:
$$\text{arc length}=\frac{\text{central angle}}{360^{\circ}}\times \text{circumference}$$
$latex =\frac{120^{\circ}}{360^{\circ}}\times (2\pi (6))$
$latex =\frac{1}{3}\times 37.7$
$latex =12.57$
The length of the arc is equal to 12.57 m.
EXAMPLE 4
What is the length of the arc that has a radius of 3 m and an angle of 1.5 radians?
Solution
In this case, we have the length of the radius $latex r = 3$ and the measure of the arc in radians $latex \theta = 1.5$. Therefore, we have to use the second formula with these values:
$latex s=\theta r$
$latex =(1.5)(3)$
$latex =4.5$
The length of the arc is 4.5 m.
EXAMPLE 5
If an arc has an angle of 2.1 radians and is formed by a radius of 5 m, what is its length?
Solution
We have the radius $latex r=5$ and the angle of the arc $latex \theta = 2.1$. Using the second formula with these values, we have:
$latex s=\theta r$
$latex =(2.1)(5)$
$latex =10.5$
The length of the arc is 10.5 m.
Arc of a circumference – Practice problems
Practice using the formulas and methods above to find arc lengths and solve the following problems. Look at the solved examples above if you need help.
See also
Interested in learning more about circles and circumferences? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
