Vertical projectile motion is a particular case of projectile motion, where an object is thrown vertically upwards or downwards, with no horizontal component of velocity. In this type of motion, the object is subject only to the force of gravity, which acts downward with a constant acceleration denoted by “g” (approximately 9.8 m/s² on Earth).
Here, we will learn about the formulas that we can use to predict the behavior of objects in vertical projectile motion, and we will use them to solve problems related to this type of motion.
PHYSICS

Relevant for…
Learning about vertical projectile motion in physics with exercises.
PHYSICS

Relevant for…
Learning about vertical projectile motion in physics with exercises.
Formulas for vertical projectile motion
Vertical projectile motion is any vertical motion accelerated under the action of gravity, whether the object travels upward or downward (free fall). Air resistance, which tends to slow the motion, is ignored. This is an extremely common motion in nature and everyday life.
Vertical projectile motion is considered free fall even if it has initial velocity since free fall is the movement of an object accelerated under the action of gravity alone.
Therefore, the equation for position as a function of time in a vertical projectile motion is the same as that for any rectilinear motion with constant acceleration. This acceleration is denoted $latex g$ and commonly its value is $latex g= 9.8\hspace{1mm}\dfrac{m}{s^2}$, assuming that the movement occurs in the vicinity of the Earth.
Vertical projectile motion: formula for position.
In all cases, if a reference system is chosen, in which the vertical downward direction is negative, the equation for the position of an object as a function of time, acquires the form:
$$y(t)=y_{0}+v_{0}t-\frac{1}{2}gt^2$$
However, in some cases, it will be more convenient to take the vertical downward direction as positive, so care must be taken to be consistent with the choice of signs.
In the equation shown, $latex y(t)$ denotes the vertical position as a function of elapsed time, and $latex y_{0}$ is the initial position, which can be chosen to be equal to 0 at the launch point, simplifying equation a:
$$y(t)=v_{0}t-\frac{1}{2}gt^2$$
The sign of the initial velocity can be positive or negative, depending on whether the object is propelled upward or downward. That is, if the object is propelled upwards, the initial velocity is positive, and as the projectile ascends, its magnitude decreases little by little until it stops. At that point, the object reaches its maximum height.
Numerous applications require knowledge of this maximum height, for which it is not difficult to develop an expression:
Vertical projectile motion: formula for maximum height.
Starting from the equation relating velocity and position for a uniformly accelerated motion:
$$v^2 =v_0^2 – 2gy$$
Making $latex v=0$, results in the maximum height $latex y_{max}$, given by:
$$0 =v_0^2 – 2gy_{max}$$
Therefore:
$$y_{máx}=\frac{v_0^2}{2g}$$
As can be seen, the maximum height depends on the initial velocity given to the projectile. The higher this velocity, the more height the object will reach.
Projectile vertical motion: formula for maximum time.
The maximum time is the time it takes for the projectile to reach its maximum height. It can be calculated from the equation relating velocity and time:
$$v=v_0-gt$$
When the projectile reaches the maximum height, it momentarily stops and begins to descend, just there the maximum time $latex t_{max}$ is reached:
$$0=v_0-gt_{max}$$
$$t_{max}=\frac{v_0}{g}$$
The higher the initial velocity of the object, the longer it will take to reach the maximum height.
Solved exercises on vertical projectile motion in Physics
Note: In the exercises that follow, air resistance is ignored and the value of the acceleration of gravity is taken as $latex g=9.8\frac{m}{s}$.
EXERCISE 1
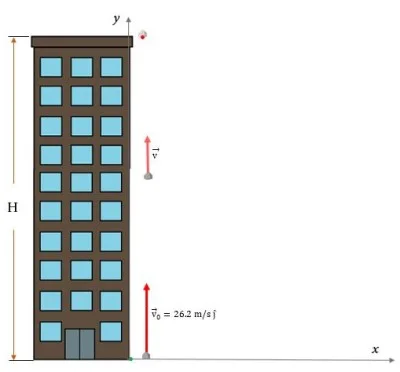
A stone is thrown vertically upward with an initial speed of 26.2 m/s, which arrives just at the edge of the roof of a building. Calculate:
a) The height H of the building.
b) The time it remains in the air.
c) How many stories does the building have? Assume that each floor is 3.5 m high.
Solution
a) To find the height of the building, knowing the initial velocity, we use:
$$h_{max}=H=\frac{v_0^2}{2g}$$
The reference system is used with the origin at the starting point and vertical direction upward positive.
Substituting the given values, we get:
$$H=\frac{\left(26.2\hspace{1mm}\dfrac{m}{s}\right)^2}{2\times 9.8\hspace{1mm}\dfrac{m}{s^2}}=35.02\hspace{1mm}m$$
b) The time duration can be found from:
$$t=\frac{v_0}{g}$$
$$t=\frac{26.2\hspace{1mm}\dfrac{m}{s}}{9.8\hspace{1mm}\dfrac{m}{s^2}}=2.7\hspace{1mm}s$$
c) Dividing the height of the building by the height of each floor, results in n, the number of floors:
$$n=\frac{35.2}{3.5}\approx 10\hspace{1mm}floors$$
EXERCISE 2
A ball is thrown vertically upwards to reach a maximum height of 20 m.
a) What is the initial velocity to be provided?
b) How long will it last in the air?
Solution
a) From the equation that relates the maximum height to the initial velocity, we solve for initial velocity:
$$h_{max}=\frac{v_0^2}{2g}\Rightarrow v_0=\sqrt{2gh_{max}}$$
Substituting the value given in the statement for the maximum height, we obtain:
$$v_0=\sqrt{2\times\hspace{1mm}9.8\dfrac{m}{s^2}\times 20\hspace{1mm}m}=19.8\dfrac{m}{s}$$
b) Since the ball returns to its starting place, the time it will last in the air, or flight time $latex t_{flight}$, is twice the time it takes to reach the maximum height $latex t_{max}$:
$$t_{flight}=2\cdot t_{max}=\frac{2v_0}{g}=\frac{2\times 19.8\dfrac{m}{s}}{9.8\dfrac{m}{s^2}}=4.04\hspace{1mm}s$$
EXERCISE 3
From the roof of a building, located 10 m above the ground, two objects are launched vertically upwards, with a time interval of 2 s between each launch. The initial velocity of the first object is 80 m/ and that of the second object is 100 m/s.
a) After how long will the objects be at the same height?
b) What height will this be?
c) What will be the velocity of each object at that instant?
Solution
a) Let $latex y_1$ and $latex y_2$ be the respective positions of each object, and let $latex t_1$ and $latex t_2$ be their respective times. Calling $latex t$ the time of the first object, the time of the second will be delayed by 2 seconds, so $latex t_2=t-2$.
For the encounter to occur, the positions and times of the objects must be the same:
$$y_1=y_2\Rightarrow v_{01}t-\frac{1}{2}gt^2= v_{02}(t-2)-\frac{1}{2}g(t-2)^2$$
$$ 80t-4.9t^2= 100(t-2)-4.9(t-2)^2$$
Then, the following equation is obtained:
$$ 80t-4.9t^2= 100t-200-4.9t^2+19.6t-19.6$$
$$-20t-19.6t=-200-19.6$$
$$39.6t=219.2\Rightarrow t =\frac{219.6}{39.6}\hspace{1mm}s=5.5\hspace{1mm}s$$
b) The height can be found by substituting this result into the equation of the position of the objects, for example:
$$y_1=80t-4.9t^2=(80\times 5.5-4.9\times 5.5^2)\hspace{1mm}m=291.8\hspace{1mm}m $$
c) The equation of the velocity for any of the objects is:
$$v(t)=v_0-gt$$
So, for each one:
$$v_1=80\frac{m}{s}-\left(9.8\frac{m}{s^2}\times 5.5\hspace{1mm}s\right)=26.1\hspace{1mm}\frac{m}{s}$$
$$v_2=100\frac{m}{s}-\left(9.8\frac{m}{s^2}\times 5.5\hspace{1mm}s\right)=46.1\hspace{1mm}\frac{m}{s}$$
EXERCISE 4
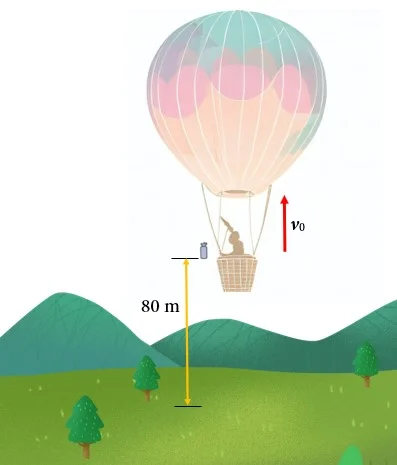
A balloon is at 80 m, ascending with a constant speed of 58 m/s, when it suddenly releases a package.
a) How long does it take for the package to reach the ground?
b) What is its maximum height?
Solution
a) The package leaves the balloon with the initial velocity $latex v_{0}$. Taking the origin of the coordinate system at the place where the package is released, the position equation is:
$$y(t)=v_0t-\frac{1}{2}gt^2$$
And substituting the initial velocity indicated in the statement, it results:
$$y(t)=58t-4.9t^2$$
The ground is in the position $latex y=-80\hspace{1mm}m$, which leads to the following quadratic equation:
$$-80=58t-4.9t^2$$
Whose solutions are:
$latex t_1=-1.25$
$latex t_2=13.1$
Only the positive solution makes sense, therefore, the package lasts in the air for a time $latex t_{flight}=13.1\hspace{1mm}s$.
b) Since the initial velocity of the package is upward, it is taken as positive. The package will climb a certain height before descending.
The maximum height with respect to the position its released is:
$$h_{max}=\frac{v_0^2}{2g}=\frac{\left(58\dfrac{m}{s}\right)^2}{2\times 9.8\dfrac{m}{s^2}}=171.6\hspace{1mm}m$$
Then, the maximum height, measured with respect to the ground is:
$$H_{max}=(171.6+80)\hspace{1mm}m=251.6 \hspace{1mm}m$$
EXERCISE 5
A test rocket is launched vertically with an initial velocity of 75.0 m/s and moves away from the launch pad with an acceleration of 5.50 m/s2. After a while, the rocket exhausts its fuel and its engine shuts down at an altitude of 1.20 km, after which it is released to the action of gravity.
a) How long does the rocket stay in the air?
b) What is the maximum altitude reached by the rocket?
c) What is the velocity of the rocket just before it hits the ground?
Solution
a) The movement is vertical and occurs in two stages: the first in which the rocket is propelled by the acceleration provided by its fuel and ascends $latex 1.20\hspace{1mm} km = 1200 \hspace{1mm}m$ .
The second begins when the fuel runs out and the rocket is under the action of gravity.
In the first stage, the acceleration propels the rocket upward and is assigned a + sign, while in the second stage, the acceleration is that of gravity, directed vertically downward and with a – sign.
First stage
The equation for position in the first stage is:
$$ y=75t+\left(\frac{1}{2}\right)5.5t^2=75t+2.75t^2$$
Where the origin of the coordinate system has been taken at the launch point.
Solving the equation in $latex t$ for $latex y=1200$, results:
$$2.75t^2+75t-1200=0$$
The positive solution is:
$$t=11.3\hspace{1mm}s$$
By that time, the rocket’s velocity is:
$$v=75+5.5t=(75+5.5\times 11.3)\hspace{1mm}\frac{m}{s}=137.15\hspace{1mm}\frac{m}{s} $$
Second stage
The next stage takes place under the action of gravity and starts with the speed it had at the end of the first stage, which has just been calculated.
The new position equation will be:
$$ y=1200+137.15t-4.9t^2$$
The time required to return to $latex y = 0$ is obtained by solving the equation:
$$ 1200+137.15t-4.9t^2=0$$
Whose solution is:
$$t=35.0\hspace{1mm}s$$
Therefore, the rocket stayed in the air for a time $latex t_{total}$:
$$t_{total}=11.3\hspace{1mm}s+35.0\hspace{1mm}s=46.3\hspace{1mm}s$$
b) During the first stage of the movement, the rocket ascended $latex h_1= 1200\hspace{1mm}m$. So, now we calculate the height it reaches during the second stage, which we will call $latex h_2$:
$$h_2=h_{max}=\frac{v_0^2}{2g}=\left(\frac{137.15^2}{2\times 9.8}\right)\hspace{1mm}{m}=964.6\hspace{1mm}{m}$$
Therefore:
$$h_2=964.6\hspace{1mm}{m}$$
The rocket ascends to a total height $latex H$ of:
$$H=1200\hspace{1mm}{m}+964.6\hspace{1mm}{m}=2164.6\hspace{1mm}{m}$$
c) The equation for the velocity in the second stage is:
$$v(t)=137.15-9.8t$$
Therefore, the velocity when it reaches the ground is:
$$v(t)=(137.15-9.8\times35.0)\hspace{1mm}\frac{m}{s}=-205.85\hspace{1mm}\frac{m}{s}$$
EXERCISE 6
A ball is dropped from the roof of an 80 m building, and two seconds later, another identical ball is thrown from the ground, vertically upwards, with initial velocity 20 m/s. Calculate:
a) At what instant do they cross?
b) At what height does the crossing occur?
Solution
a) The origin of the coordinate system can be chosen on the roof so that the ground is at the position $latex y_{ground}=-80\hspace{1mm}m$.
For ball 1, the position equation is:
$latex y_1=-4.9t^2$
For ball 2, which starts 2 seconds later than ball 1 and has an initial upward velocity of $latex 20\frac{m}{s}$, the position equation is:
$latex y_2=-80+20(t-2)-4.9(t-2)^2$
For the balls to intersect, they must occupy the same vertical position:
$$y_1=y_2\Rightarrow -4.9t^2=-80+20(t-2)-4.9(t-2)^2$$
Using algebra:
$$-4.9t^2=-80+20t-40-4.9(t^2-4t+4)\Rightarrow $$
$$-4.9t^2=-80+20t-40-4.9t^2+19.6t-19.6$$
After simplifying like terms:
$$39.6t=139.6\Rightarrow t=\frac{139.6}{39.6}\hspace{1mm}s=3.5\hspace{1mm}s$$
b) The location of the intersection can be found by substituting this time in any of the position equations, for example:
$$ y_1=(-4.9\times 3.5^2)\hspace{1mm}m=-60\hspace{1mm}m$$
It means that, measured from the ground, the height at which the intersection occurs is:
$$h_{intersection}=(80-60)\hspace{1mm}m=20\hspace{1mm}m$$
EXERCISE 7
Wonder Woman is on a bridge, while a flatbed truck is heading towards her on the highway below, at a constant speed of 18 m/s. When she calculates it is opportune, Wonder Woman launches herself from the bridge and lands with great precision 10.0 m below, right on the roof of the truck. Calculate how far the truck was from the bridge when she jumped, in the following cases:
a) If she started with zero initial velocity.
b) She started vertically downward with an initial speed of 2 m/s.

Solution
To solve the exercise, it is necessary to take into account that there are two objects in motion. The first is the truck, with uniform rectilinear motion in the horizontal direction, and the second is the wonder woman, whose motion is accelerated in the vertical direction.
For Wonder Woman to land safely on the platform of the truck, the time it takes for the truck to travel the distance $latex \Delta x$ that separates it from the bridge must be equal to the time it takes for her to fall the 10 m height .
This time is as follows:
$$y=\frac{1}{2}gt^2\Rightarrow t=\sqrt{\frac{2y}{g}}$$
$$t=\sqrt{\frac{2\times 10\hspace{1mm}m}{9.8\hspace{1mm}\dfrac{m}{s^2}}}=1.43\hspace{1mm}s$$
During this time, the truck, which is in uniform rectilinear motion, will travel this distance:
$$\Delta x=18\hspace{1mm}\dfrac{m}{s}\times1.43\hspace{1mm}s= 25.74\hspace{1mm}m$$
And the answer is that the truck was 25.74 meters away from the bridge when Wonder Woman jumped off it.
b) If Wonder Woman starts with a certain initial velocity, the time it takes to fall the 10 meters is less. In the calculations that follow, for convenience the downward vertical position is assumed to be positive:
$$y=v_0t+\frac{1}{2}gt^2$$
$$10=2t+4.9t^2$$
$$4.9t^2+2t-10=0$$
Whose solution is:
$$t=1.24\hspace{1mm}s$$
In such a case, the truck must be at the following distance, also shorter than in the previous case:
$$\Delta x=18\hspace{1mm}\dfrac{m}{s}\times1.24\hspace{1mm}s= 22.32\hspace{1mm}m$$
Vertical projectile motion – Practice problems


Write the answer in the input box.
See also
Interested in learning more about motion in physics? You can take a look at these pages:



