Motion with constant acceleration is a type of motion in which the speed of an object changes constantly over time. This means that the acceleration is constant and different from zero. This type of motion can be observed in everyday situations, such as a car braking or accelerating, or an object falling under the influence of gravity.
The most commonly used equations to describe motion with constant acceleration are:
- Velocity equation: v(t) = v₀ + at
- Position equation: x(t) = x₀ + v₀t + (1/2)at²
- Velocity equation as a function of position: v² = v₀² + 2a(x – x₀)
PHYSICS
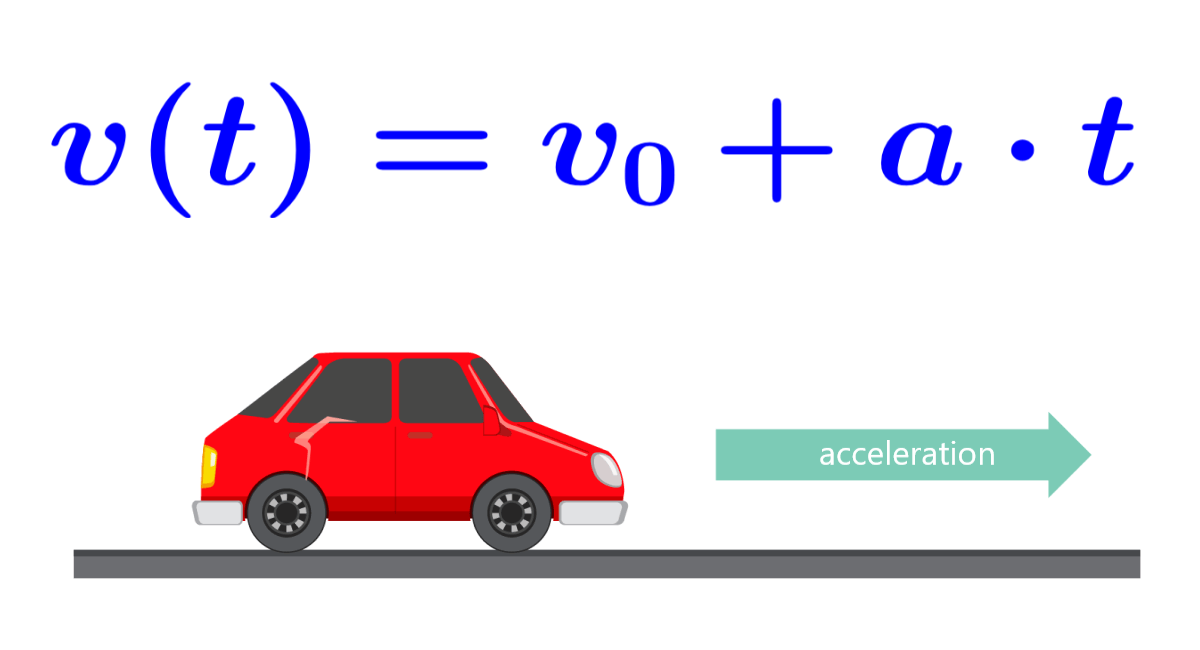
Relevant for…
Learning about motion with constant acceleration with exercises.
10 Solved Exercises on Motion with Constant Acceleration
EXERCISE 1
A car that is initially at rest begins to move (in a straight line) increasing its speed uniformly for 4 seconds, after which it acquires a speed of 36 km/h. What acceleration value did the car have during that period? (Express the result in $latex \dfrac{m}{s^2}$)
Solution
Acceleration is the change in velocity per unit time. Since we know that this is rectilinear motion with constant acceleration, then the acceleration is calculated by taking the difference between the final velocity minus the initial velocity and dividing by the length of time during which the motion occurred:
$$a=\dfrac{V_f-V_i}{\Delta t}$$
The final speed of the car is $latex V_f=36 \dfrac{km}{h}$ which is equivalent to:
$$V_f=\dfrac{36}{3.6} \dfrac{m}{s}=10 \dfrac{m}{s}$$
Then the acceleration of the car during its movement was:
$$a= \dfrac{(10 \frac{m}{s} – 0 \frac{m}{s})}{4 s}= \dfrac{10 \frac{m}{s}}{4 s} = 2.5 \dfrac{m}{s^2}$$
EXERCISE 2
In the previous exercise we calculated the acceleration of a car that, starting from rest, reached the speed of $latex 10 \dfrac{m}{s}$ in a time of $latex 4 s$, resulting in an acceleration $latex a= 2.5 \dfrac{m}{s^2}$. How far will the car have traveled in that time?
Solution
In rectilinear motion with constant acceleration, the position changes with time according to the following quadratic equation:
$$ x(t) = x_0 + v_0 \cdot t + \frac{1}{2} a \cdot t^2$$
In our case, we take the initial position of the car as $latex x_0=0$ and the initial velocity as $latex v_0=0$. The acceleration $latex a=2.5 \frac{m}{s^2}$. Then the distance traveled in the $latex 4s$ is:
$$x(4)=\frac{1}{2} 2.5 \cdot 4^2=20 m$$
EXERCISE 3
We have a car that starts from rest with acceleration $latex a=2.5 \frac{m}{s^2}$. How long does it take to travel the first 10 meters? What speed will it have at that moment?
Solution
The relationship between position and time is given by:
$$ x(t) = x_0 + v_0 \cdot t + \frac{1}{2} a \cdot t^2$$
But, in this exercise we have to have $latex x_0=0 \; and \; v_0=0$ so the formula simplifies to:
$$ x(t) = \frac{1}{2} a \cdot t^2$$
It is also known that at a certain time $latex t$ the position is $latex x(t)=d=10m$. Solving the time from the previous formula we have:
$$ t=\sqrt{\dfrac{2d}{a}}$$
Then, the time taken to travel the first 10 meters is: $$t=\sqrt{ \frac{2 \cdot 10}{2.5} }=2.828 s$$
We are also asked for the speed of the car at the time it traveled the first 10 meters. For this, we use the following relationship between speed and time:
$$ v(t)=v_0+a \cdot t$$
So the speed, for that instant, is: $$ v(2.83)=0 + 2.5 \cdot 2.828=7.07 \frac{m}{s}$$
EXERCISE 4
A motorcycle is stopped at a traffic light, waiting for the light to change. At the same moment that the light changes, a car coming with a constant speed of 14 m/s crosses the traffic light. The motorcycle starts just when the light changes with a constant acceleration of 2.4 m/s2. Calculate:
a) At what point does the motorcycle catch up with the car?
b) How fast was the motorcycle at that time?
c) At what distance from the traffic light does the encounter between the motorcycle and the car occur?
Solution
We take the traffic light as position zero and the moment when the light changes as time zero. In this case, the position of the car as a function of time is given by:
$$x_c(t)=V_c \cdot t$$
While the position of the motorcycle as a function of time is:
$$x_m(t)= \frac{1}{2} a \cdot t^2$$
At the instant of encounter, which we will call $latex t^*$, both vehicles will have the same position:
$$ x_c(t^*)=x_m(t^*)$$
That is, for that instant the following equality is satisfied:
$$V_c \cdot t^* = \frac{1}{2}a \cdot {t^*}^2 $$
It follows that:
$$ t^* = \dfrac{2 V_c}{a}$$
By using the corresponding numerical values, we obtain:
a) $$ t^* = \dfrac{2 \cdot 14 \frac{m}{s}}{2.4 \frac{m}{s^2}}=11.667s$$
As the motorcycle accelerates, its speed increases linearly with time according to:
$$ v_m(t)= a \cdot t$$
At the instant the motorcycle reaches the car, its speed will be:
b) $$ v_m(t^*)= a \cdot t^*= 2.4 \frac{m}{s^2} \cdot 11.667s =28 \frac{m}{s} $$
After $latex t^*=11.667s$, both the motorcycle and the car are at the same distance from the traffic light, which is given by:
c) $$ x_c(t^*)=V_c \cdot t^*= 14 \frac{m}{s} \cdot 11.667s = 163.34 m $$
EXERCISE 5
A tennis ball is thrown from the racket at a speed of 250 km/h. Taking into account that the ball starts from rest and is only in contact with the racket for 30 milliseconds, what acceleration was the ball subjected to?
Solution
Prior to calculating the acceleration, we proceed to convert the velocity of the ball to $latex \frac{m}{s}$:
$$250 \dfrac{km}{h}=250 \dfrac{10^3 m}{3600 s}= \dfrac{250}{3.6} \dfrac{m}{s}=69.44 \frac{m}{s}$$
We will assume that the acceleration of the ball was constant, from the moment it made contact with the racquet until the moment it comes off the racquet.
In this case the acceleration is calculated by taking the quotient of the variation of the speed divided by the lapse of time during which this variation occurred:
$$a = \dfrac{\Delta V}{\Delta t}= \dfrac{69.44 \frac{m}{s}}{0.030 s}=2314.8 \frac{m}{s^2}$$
This is an enormous acceleration, if we compare it with the acceleration of gravity, which is the acceleration with which a released object falls, which is $latex g=9.8 \frac{m}{s^2}$. The acceleration of the ball was 236 times greater than the acceleration of gravity:
$$a=236g$$
This is an enormous acceleration, considering that fighter pilots momentarily lose consciousness when subjected to accelerations between $latex 3g$ and $latex 4g$. At $latex 35g$ the ribs fracture.
EXERCISE 6
The acceleration of a Formula 1 race car is significantly higher than that of a conventional vehicle, as an F1 is capable of reaching 100 km/h in just 2.8 seconds. Calculate the acceleration of an F1 car and compare it with the acceleration of gravity. Also calculate the distance the F1 travels in the first 2.8 of acceleration.
Solution
First, we convert from km/h to m/s:
$$100 \frac{km}{h}=\dfrac{100}{3.6} \frac{m}{s}=27.77 \frac{m}{s}$$
Then the acceleration is calculated as follows:
$$a = \dfrac{\Delta V}{\Delta t}= \dfrac{27.77 \frac{m}{s}}{2.8 s}=9.92 \frac{m}{s^2}$$
Compared to the acceleration of gravity, which is $latex 9.8 \frac{m}{s^2}$, the acceleration of F1 is just one hundredth greater:
$$a= 1.01g$$
In the first 2.8 seconds F1 travels a distance given by:
$$d= 0.5 \cdot a \cdot t^2= 0.5 \cdot 9.92 \frac{m}{s^2} \cdot (2.8 s)^2 = 39 m $$
EXERCISE 7
The graph in the figure represents the velocity as a function of time of a cyclist moving along a straight line. Describe the movement of the cyclist. Calculate the distance traveled in the first three seconds and then between three seconds and five seconds. Find the braking acceleration.

Solution
The cyclist starts his movement with a speed of 3 m/s, which he maintains during 3 s. Then, he starts to brake and in 2 seconds he goes from a speed of 3 m/s to a speed of 0 m/s.
The distance traveled in the first 3 s is the area under the rectangle: $latex d_1 = v \cdot t = 3 m/s \cdot 3 s = 9m$.
In the next 2 seconds, the distance traveled is the area under the triangle: $latex d_2 = ( 3 m/s \cdot 2 s)/2 = 3m$.
The total distance traveled, from when the movement starts until it stops, is: $latex d= d_1+ d_2= 12m$.
Between 3s and 5s the cyclist’s speed decreases uniformly, at a rate of 3 m/s in 2 s. This means that his acceleration is:
$$ a=\dfrac{V_f-V_i}{t_f-t_i}=\dfrac{0 m/s – 3 m/s}{5 s – 3 s}= \dfrac{-3 m/s}{2 s}= -1.5 \frac{m}{s^2}$$
The negative sign tells us that the acceleration goes in the opposite direction to the velocity (which has been taken as the positive direction). Therefore, between 3s and 5s the cyclist decreases his speed at the rate of 1.5 m/s in each second.
EXERCISE 8
An electric car starts from rest and uniformly increases its speed at a rate of 2.0 m/s every second, following a straight path, until it reaches 20 m/s. It then maintains that speed for 2 seconds, until it sees a red traffic light and starts braking at a rate of 1 m/s2 until it stops.
Plot the motion of the car on a speed – time graph. Calculate the elapsed time from when it started moving until it stopped. Find the total distance traveled.
Solution
To plot the graph, we need to know how long it takes to reach 20 m/s. For this, we will use the following expression:
$$V(t)=V_0 + a \cdot t$$
We know that $latex V(t)=20 m/s$, the initial speed $latex V_0=0$, and that the acceleration is $latex a=2 m/s^2$. Therefore, we must solve for the time, $latex t$:
$$t= \dfrac{V(t)}{a}=\dfrac{20 m/s}{2 m/s^2}= 10 s$$
The car maintains the speed reached for 2 more seconds. From there it begins to brake with acceleration $latex a=-1 m/s^2$, this will take a period $latex \Delta t$ given by:
$$ \Delta t= \dfrac{0 m/s – 20 m/s}{-1 m/s^2}= 20 s$$
With this data we can construct the speed – time graph:

The carriage was moving for 32 sec.
The total distance traveled is the area under the v-t graph, which can be calculated in three sections as follows:
$$ d_1= \dfrac{ 20 m/s \cdot 10 s}{2}=100 m$$
$$ d_2= 20 m/s \cdot 2 s = 40 m$$
$$ d_3= \dfrac{20 m/s \cdot 20 s}{2}=200m$$
The total distance traveled by the electric car was:
$$ d= d_1+d_2+d_3= 100m + 40m + 200m = 340 m$$
EXERCISE 9
A car is waiting for the red light to change. When it turns green, the car accelerates, uniformly, at a rate of $latex 2 m/s^2$ for $latex 6s$, after which it continues at constant speed. Just as the car starts, a truck coming from behind with a constant speed of $latex10 m/s$ overtakes it.
In how long and at what distance (from the traffic light) does the car catch up with the truck? What is the speed of the car at that time?
Solution
The equation that gives the position of the car as a function of time is:
$$x_a(t)= \frac{1}{2} \cdot 2 \frac{m}{s^2} \cdot t^2$$
and the position of the truck at any instant $latex t$ is:
$$x_c(t)= 10 \frac{m}{s} \cdot t$$
If we call $latex t_e$ the instant of encounter, then it is true that for that instant the positions of the car and the truck are equal:
$$x_a(t_e)=x_c(t_e) \Rightarrow {t_e}^2=10 t_e$$
The solutions for this equation are: $latex t_e=0$ and $latex t_e=10s$. The first is when the truck passes the car at the traffic light and the second is when the car overtakes the truck, which is the solution that interests us.
That is, the car catches up to the truck at $latex 10s$ at a distance of $$ x_a(10s)=10^2 m= 100m$$
At that instant, the car has a speed given by:
$$V_a(t_e) = 2 \frac{m}{s^2} \cdot 10 s = 20 \frac{m}{s}$$

EXERCISE 10
An unidentified object moves with constant acceleration. It is observed that in the first 2 seconds, it travels a distance of 55m, while in the next 2 seconds it travels 77m. Determine at what acceleration the object is moving and what its initial speed was. Assuming it maintains its state of motion, how far will it travel in the next 2 seconds?
Solution
We know that the object moves with constant acceleration $latex a$. We also consider fixed time intervals of $latex \Delta t=2s$. In the first period, the object moves $latex \Delta x_1=55m$, in the second period (also 2s) the object moves $latex \Delta x_2=77m$.
The relationship between these quantities is as follows:
$$ \Delta x_1=V_{01} \cdot \Delta t + \frac{1}{2} \cdot a \cdot {\Delta t}^2 \; ; \; (ec.1)$$
$$ \Delta x_2=V_{02} \cdot \Delta t + \frac{1}{2} \cdot a \cdot {\Delta t}^2 \; ; \; (ec.2)$$
Where $latex V_{01}$ is the initial velocity in the first section, while $latex V_{02}$ is the initial velocity in the second section. However, the initial velocity of the second section is the final velocity of the first section, which leads us to write the following relationship:
$$ V_{02} = V_{01} + a \cdot \Delta t \; ; \; (ec.3)$$
Substituting the above expression, in the equation that gives the displacement of the second section, we are left with the following equation after operation and simplification:
$$ \Delta x_2=V_{01} \cdot \Delta t + \frac{3}{2} \cdot a \cdot {\Delta t}^2 \; ; \; (ec.4)$$
Subtracting(eq.4) minus (eq.1) we are left with:
$$ 22= a \cdot {\Delta t}^2=a \cdot 2^2 \; \Rightarrow \; a=\frac{11}{2} $$
Then using (eq.1) we can obtain $latex V_{01}$:
$$ 55=V_{01} \cdot 2 + \frac{1}{2} \cdot \frac{11}{2} \cdot 2^2 \; \Rightarrow \; V_{01}=22 $$
Now we are ready to calculate how far the strange object travels in the third period of 2 seconds. We will do this by calculating the total displacement that the object had in $latex 3 \cdot \Delta t = 6 s$:
$$ \Delta x(6s)= V_{01} \cdot 6s + \frac{1}{2} \cdot a \cdot {6s}^2= 22 \cdot 6 + \frac{1}{2} \cdot \frac{11}{2} \cdot 6^2=231m$$
Then in the third lapse of 2 seconds, it traveled a distance of $latex 231 -(55+77) = $99m.
In summary, for the unidentified object we discover that its acceleration is $latex \frac{11}{2} \frac{m}{s^2}$, that its motion begins with a speed of $latex 22 \frac{m }{s}$ and that in every period of 2 seconds, it moves following the following sequence:
$$ 55m; \; 77m; \; 99m$$
Motion with Constant Acceleration – Practice Problems


Write the answer in the input box.
See also
Interested in learning more about motion in physics? You can take a look at these pages:



