One important aspect in the study of projectiles is the range of a projectile. The ‘range of a projectile’ defines the horizontal distance a launched object will travel under the influence of gravity before it returns to the same vertical position.
In this article, we will explore the factors affecting the range and the equations we can use to calculate it. Then, we will look at a few examples with detailed solutions.
Equation for the range of a projectile
The range of a projectile is the horizontal distance that the projectile travels from its launch point to the point where it returns to the launch height. The range is a crucial component of projectile motion because it describes how far the object will travel given a specific initial velocity and launch angle.
The range of a projectile is dependent on several factors: the initial speed at which the object is launched, the angle of launch, and the acceleration due to gravity.
The equation for the range ($latex R$) of a projectile, launched at an initial speed ($latex u$) at an angle ($latex \theta$) to the horizontal, under ideal conditions (no air resistance), and assuming the start and end heights are the same, is given by:
$$R = \frac{u^2\sin(2\theta)}{g}$$
where:
- $latex R$ is the range or horizontal distance travelled,
- $latex u$ is the initial velocity,
- $latex g$ is the acceleration due to gravity (about 9.81 m/s² on Earth’s surface), and
- $latex \theta$ is the angle between the direction of the initial velocity and the horizontal.
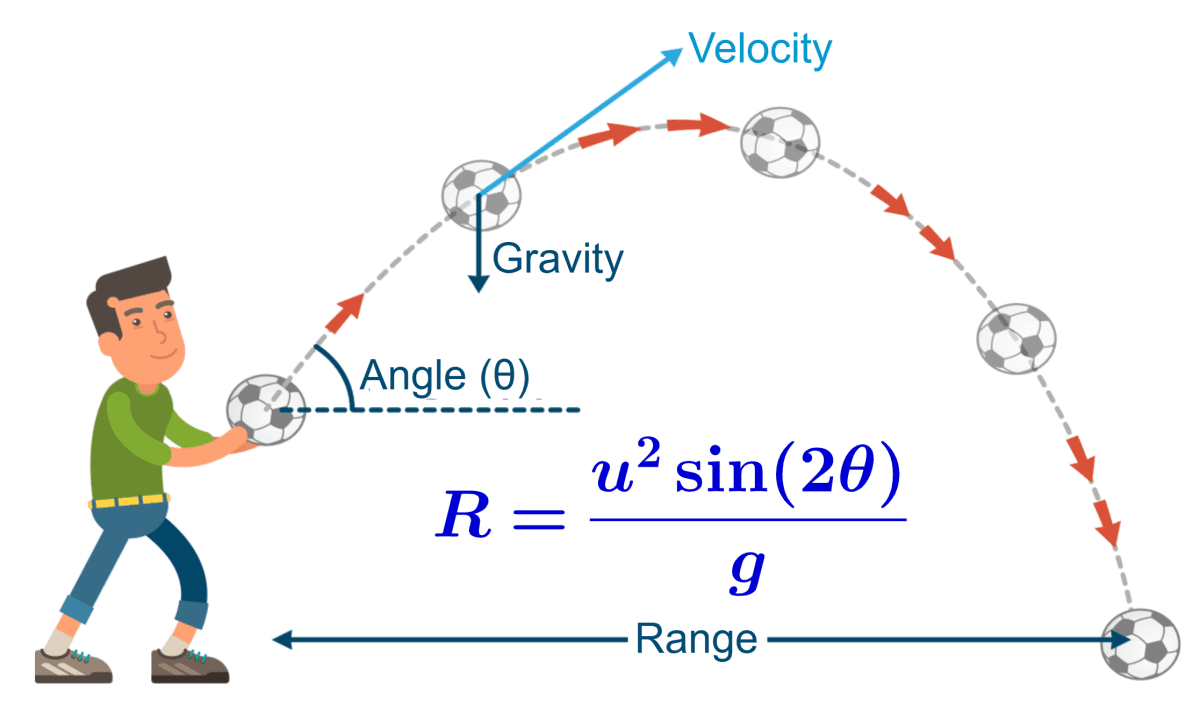
This equation is derived by combining the equations which govern the vertical and horizontal displacements of a projectile. For the vertical component or height, we have:
$latex h=ut \sin (\theta)-\frac{1}{2}gt^2$
Using this, we can find the time it takes for the projectile to hit the ground again. This happens when $latex h=0$:
$latex 0=ut \sin (\theta)-\frac{1}{2}gt^2$
$latex \frac{1}{2}gt^2=ut \sin (\theta)$
Solving for time:
$$t=\frac{2u\sin(\theta)}{g}$$
Now, for the horizontal component, we have:
$latex s=ut\cos(\theta)$
The horizontal displacement or range, $latex R$ happens when the projectile hits the ground. That is, when $latex h=0$ and when $latex t=\frac{2u\sin(\theta)}{g}$. Then,
$$R=u\times \frac{2u\sin(\theta)}{g}\times \cos(\theta)$$
$$= \frac{u^2\times 2\sin(\theta) \cos(\theta)}{g}$$
Using the trigonometric substitution $latex \sin(2\theta)=2\sin(\theta)\cos(\theta)$, we have:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
Impact of Various Factors on the Range of a Projectile
The range of a projectile is influenced by several factors, including the initial velocity, launch angle, and gravity.
Effect of Changes in Initial Velocity on Range
Assuming the launch angle and gravity remain constant, a higher initial velocity results in a larger range. This is because the initial velocity provides the projectile with its initial kinetic energy, and a higher initial velocity gives it more energy to overcome gravity for a longer distance.
Impact of the Angle of Projection on Range
At a fixed initial velocity and gravitational force, the range initially increases as the angle increases. However, beyond a certain point (45 degrees in the absence of air resistance), the range begins to decrease as the angle increases further. This is because a larger portion of the initial velocity is then directed upwards, counteracting gravity for longer, but not contributing as much to horizontal motion.
Influence of Gravity on the Range
In an environment with stronger gravity, the range of a projectile is shorter, assuming the launch angle and initial velocity remain the same. This is because a stronger gravitational pull brings the projectile down to the earth faster, thereby reducing the horizontal distance covered.
The Maximum Range at 45 degrees
For a given initial velocity, the maximum range of a projectile is achieved when it is launched at an angle of 45 degrees. This is a special case that results from the balance between the horizontal and vertical components of the initial velocity.
When a projectile is launched, the initial velocity is split into two components: the vertical component (which counteracts gravity) and the horizontal component (which contributes to the range).
If the launch angle is 45 degrees, these two components are equal, creating an optimal balance. This results in the maximum range since the projectile gets enough lift to stay in the air while also having enough horizontal velocity to cover a large distance.
Solved examples on the range of a projectile
EXAMPLE 1
A football is kicked at an angle of 30° with the horizontal at an initial speed of 25 m/s. How far does the football travel horizontally? Assume no air resistance and take $latex g = 9.8$ m/s².
Solution
To calculate the range of the projectile, we need the initial velocity and the angle with the horizontal. As we have that information, we can just use the equation given above:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
Using the given values:
$$R= \frac{25^2\times \sin(2\times 30^{\circ}) }{9.8}$$
$$= \frac{625 \times \sin(60^{\circ}) }{9.8}$$
$$= \frac{625 \times 0.866 }{9.8}$$
$latex R = 55.23$
So, the football will land approximately 55.23 meters away from the kick-off point.
EXAMPLE 2
A baseball is hit at a speed of 40 m/s at an angle of 30° with respect to the horizontal. How far does the baseball travel before it hits the ground? Assume no air resistance and use $latex g = 9.8$ m/s².
Solution
Again, we can use the formula for the range of a projectile:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
Now, we substitute the given values:
$$R= \frac{40^2\times \sin(2\times 30^{\circ}) }{9.8}$$
$$= \frac{1600 \times \sin(60^{\circ}) }{9.8}$$
$$= \frac{1600 \times 0.866 }{9.8}$$
$latex R = 141.39$
The baseball will travel approximately 141.39 meters before it hits the ground.
EXAMPLE 3
A golfer hits a golf ball at an angle of 35° horizontally with an initial speed of 60 m/s. How far will the golf ball travel horizontally?
Solution
The horizontal distance of the golf ball can be found using the equation for the range:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
Using the given values:
$$R= \frac{60^2\times \sin(2\times 35^{\circ}) }{9.8}$$
$$= \frac{3600\times \sin(70^{\circ}) }{9.8}$$
$$= \frac{3600 \times 0.94 }{9.8}$$
$latex R = 345.31$
The golf ball will travel approximately 345.31 meters
EXAMPLE 4
An athlete throws a javelin with an initial speed of 33 m/s at an angle of 35° to the horizontal. What is the range of the javelin throw? Assume no air resistance.
Solution
As we have the initial speed and the angle to the horizontal, we can substitute these values into the equation for the range:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
$$R= \frac{33^2\times \sin(2\times 35^{\circ}) }{9.8}$$
$$= \frac{1089\times \sin(70^{\circ}) }{9.8}$$
$$= \frac{1089 \times 0.94}{9.8}$$
$latex R = 104.46$
The range of the javelin throw is approximately 104.46 meters.
EXAMPLE 5
How far does the water travel in a fountain that shoots water at a speed of 10 m/s at an angle of 40° to the horizontal?
Solution
The range of the water in the water fountain can be found using the equation:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
Substituting the given values:
$$R= \frac{10^2\times \sin(2\times 40^{\circ}) }{9.8}$$
$$= \frac{100\times \sin(80^{\circ}) }{9.8}$$
$$= \frac{100 \times 0.985 }{9.8}$$
$latex R = 10.05$
Therefore, the water will travel approximately 10 meters before it hits the ground.
EXAMPLE 6
A cannon can fire a cannonball with a maximum speed of 500 m/s. What is the maximum range of the cannonball, and at what angle should the cannon be aimed to achieve this range? Ignore air resistance and take $latex g = 9.8$ m/s².
Solution
For maximum range, the cannon should be aimed at an angle of 45° to the horizontal. Using this angle, we calculate the maximum range using the formula:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
Using the given values:
$$R= \frac{500^2\times \sin(2\times 45^{\circ}) }{9.8}$$
$$= \frac{250000\times \sin(90^{\circ}) }{9.8}$$
$$= \frac{250000\times 1}{9.8}$$
$latex R = 25510.2$
Therefore, to achieve the maximum range, the cannon should be aimed at an angle of 45° to the horizontal, and the cannonball will travel approximately 25.5 kilometers.
EXAMPLE 7
A golfer can hit a golf ball with an initial speed of 70 m/s. What is the maximum range the golf ball can travel? Ignore air resistance and use $latex g = 9.8$ m/s².
Solution
As we saw in the last example, the maximum range can be achieved when making the golf ball travel at an angle of 45° to the horizontal.
Then, we use the formula for the range of a projectile with the initial speed given:
$$R= \frac{u^2\times \sin(2\theta) }{g}$$
$$R= \frac{70^2\times \sin(2\times 45^{\circ}) }{9.8}$$
$$= \frac{4900\times \sin(90^{\circ}) }{9.8}$$
$$= \frac{4900\times 1}{9.8}$$
$latex R = 500$
The golf ball has a maximum range of approximately 500 meters.
Range of a projectile – Practice problems
Write the answer in the input box.
See also
Interested in learning more about projectile motion? You can look at these pages:
–
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
