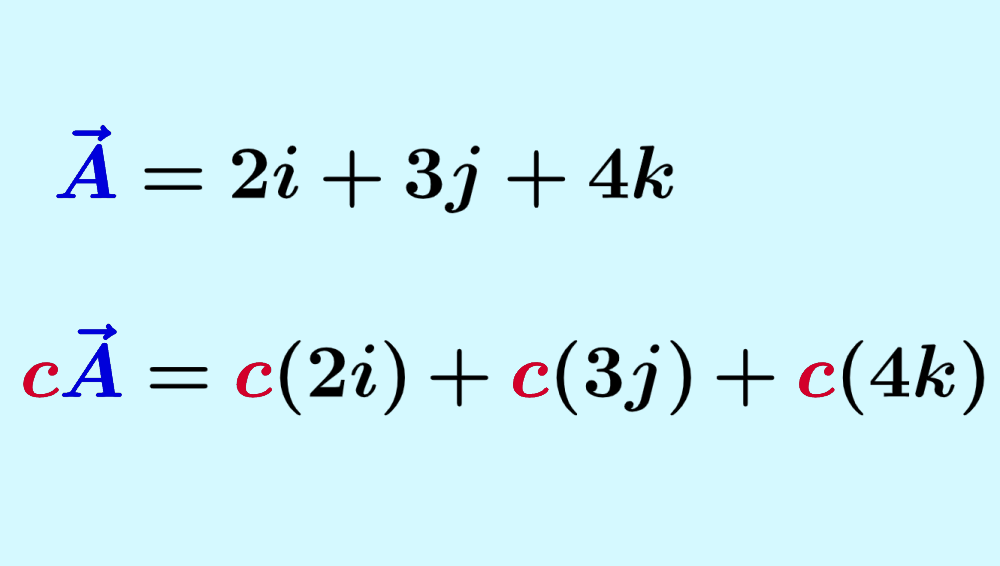The multiplication of a vector by a scalar is solved simply by multiplying the magnitude by the scalar. This is also equivalent to multiplying each of the components of the vector by the scalar.
In this article, we will learn about the multiplication of a vector by a scalar in more detail. We will solve some exercises and practice problems to apply what we have learned.
How to multiply a vector by a scalar?
To multiply a vector by a scalar, we just multiply its magnitude by the scalar. Alternatively, we multiply each of the components by the scalar.
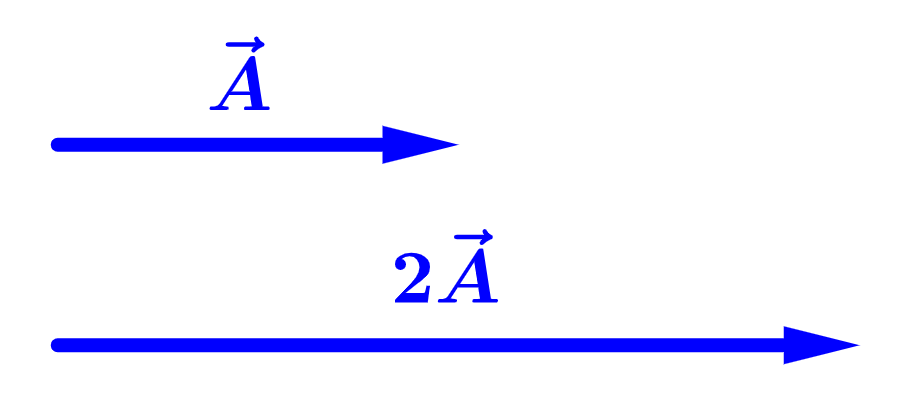
When we multiply a vector by a positive scalar, we change its magnitude, but not its direction:
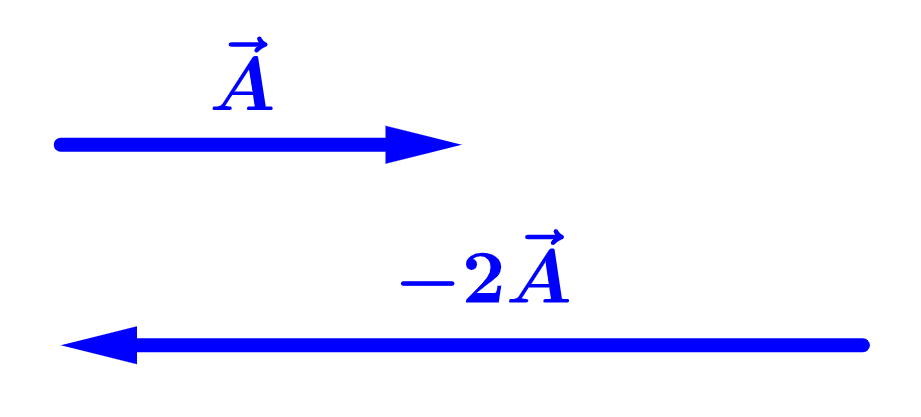
When we multiply a vector by a negative scalar, we change its magnitude and reverse its direction:
If we multiply a vector $latex \vec{A}$ by a scalar $latex k$, each component of the product $latex \vec{R}=k \vec{A}$, is the product of $latex k $ and the corresponding component of $latex \vec{A}$:
$latex R_{x}=kA_{x}$
$latex R_{y}=kA_{y}$
Note that the components are not vectors. The components of a vector are numbers and not vectors. For this reason, we use letters without arrows above them to represent them.
Solved examples on multiplication of a vector by a scalar
EXAMPLE 1
Multiply the vector $latex \vec{A} = 5i -2j+ 3k$ by the scalar $latex k = 4$.
Solution
We multiply each component of vector A by the scalar $latex k$:
$latex 5i \times 4 = 20i$
$latex -2j \times 4 = -8j$
$latex 3k \times 4 = 12k$
The resulting vector is: $latex \vec{R}= 20i -8j+ 12k$.
EXAMPLE 2
Find the product of the vector $latex \vec{B} = -1i+ 6j+ 0k$ by the scalar $latex k = -3$
Solution
By multiplying each component of vector B by the scalar $latex k$, we have:
$latex -1i \times -3 = 3i$
$latex 6j \times -3 = -18j$
$latex 0k \times -3 = 0k$
The resulting vector is: $latex \vec{R}= 3i -18j+ 0k$.
EXAMPLE 3
Multiply the vector $latex \vec{C} = 3i -4j +7k$ by the scalar $latex k = 0.5$.
Solution
When we multiply each component of the vector C by the scalar $latex k$, we have:
$latex 3i \times 0.5 = 1.5i$
$latex -4j \times 0.5 = -2j$
$latex 7k \times 0.5 = 3.5k$
The resulting vector is: $latex \vec{R}= 1.5i -2j+ 3.5k$.
EXAMPLE 4
What is the result of multiplying the vector $latex \vec{D} = 2i -5j+ 4k$ by the scalar $latex k = 3$?
Solution
By multiplying the scalar $latex k$ by each component of the given vector, we have:
$latex 2i \times 3 = 6i$
$latex -5j \times 3 = -15j$
$latex 4k \times 3 = 12k$
The resulting vector is: $latex \vec{R}= 6i -15j+ 12k$.
EXAMPLE 5
Multiply the vector $latex \vec{E} = 7i+ 0j -3k$ by the scalar $latex k = -2$.
Solution
When we multiply each component of the vector E by the scalar $latex k$, we have:
$latex 7i \times -2 = -14i$
$latex 0j \times -2 = 0j$
$latex -3k \times -2 = 6k$
The resulting vector is: $latex \vec{R}= -14i +0j+ 6k$.
EXAMPLE 6
Multiply the vector $latex \vec{F} = -4i+ 3j+ 8k$ by the scalar: $latex k = 0.25$.
Solution
By distributing the multiplication of the scalar $latex k$ to each component of the vector, we have:
$latex -4i \times 0.25 = -1i$
$latex 3j \times 0.25 = 0.75j$
$latex 8k \times 0.25 = 2k$
The resulting vector is: $latex \vec{R}= -i +0.75j+ 2k$.
Multiplying vectors by a scalar – Practice problems
If the magnitude of a vector is 17 units and we multiply the vector by 2.5, what is the magnitude of the new vector?
Write the answer in the input box.
See also
Interested in learning more about vectors? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
