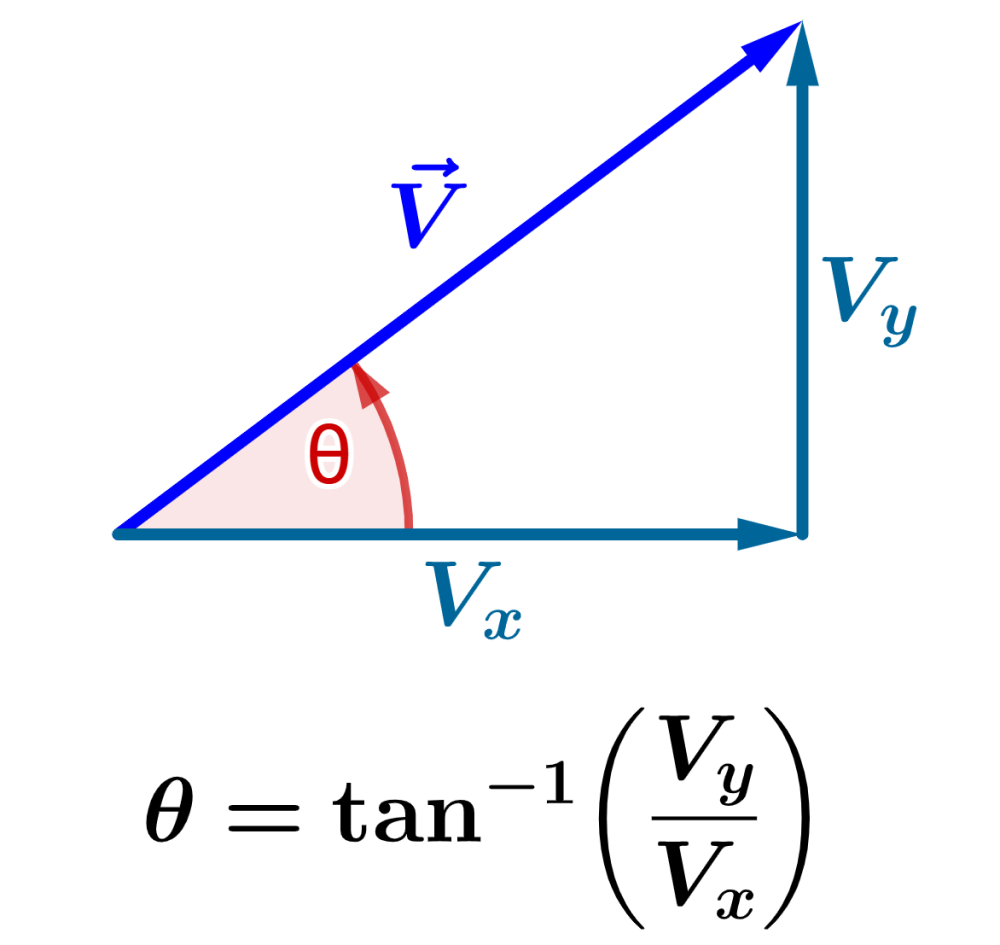The direction of a vector is the orientation of the vector in a coordinate system, usually described by the angle it forms with one of the axes. To find the direction of a 2D vector, we calculate the inverse tangent of the y-component of the vector over the x-component.
In this article, we will learn the formula that we can apply to find the direction of a vector. We will learn how to derive this formula and use it to solve some practice problems.
How to calculate the direction of a 2D vector?
In a 2D Cartesian coordinate system ($latex x, ~y$ plane), the direction of a vector can be specified by the angle it makes with the positive $latex x$ axis.
This angle is normally measured counterclockwise, with the range of possible angles being 0° to 360° (0 to 2π radians).
To calculate the angle of a vector using its components, we can use trigonometry, specifically, the tangent function.
Suppose we have the vector $latex \vec{V}$ with components $latex V_{x}$ and $latex V_{y}$ and angle $latex \theta$:
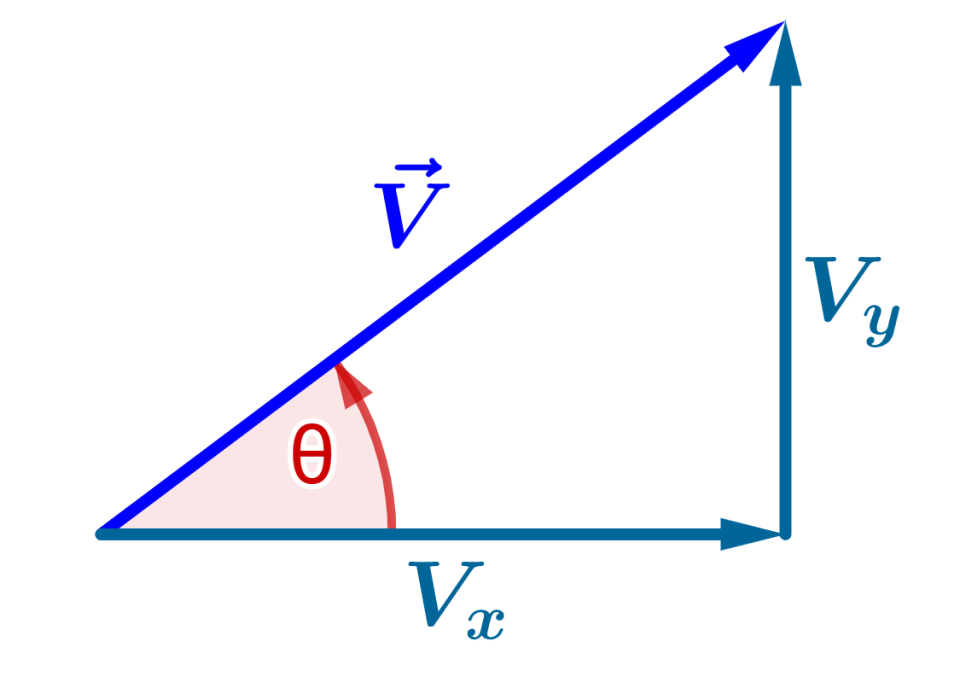
We can observe that we have a right triangle, where the vector $latex \vec{V}$ is the hypotenuse. The adjacent side (base) is equal to $latex V_{x}$, and the opposite side (height) is $latex V_{y}$.
According to the definition of the tangent function in a right triangle, we have:
$$\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}$$
In this case,
$$\tan(\theta) = \frac{V_{y}}{V_{x}}$$
To find θ, we have to take the inverse tangent (also called arctangent or atan) of both sides of the equation. Then,
$$\theta = \tan^{-1}\left(\frac{V_{y}}{ V_{x}}\right)$$
It is important to take into account the quadrant in which the vector is located since the inverse tangent function returns a result between $latex -\frac{\pi}{2}$ and $latex \frac{\pi}{2}$ (-90° to 90°).
Therefore, we can use the following table to obtain the correct angle:
| Quadrant | Value of $latex \tan^{-1}$ |
| I | Use the value of the calculator |
| II | Add 180° (π) to the calculator value |
| III | Add 180° (π) to the calculator value |
| IV | Add 360° (2π) to the calculator value |
Solved examples on the direction of a vector
EXAMPLE 1
Find the angle $latex \theta$ of the vector $latex \vec{A}$ with components $latex A_{x} = 3$ and $latex A_{y} = 4$.
Solution
We have the following components:
- $latex A_{x}=3$
- $latex A_{y}=4$
Then, we use the formula for the angle or direction of a vector:
$$\theta = \tan^{-1}\left(\frac{A_{y}}{ A_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{4}{3}\right)$$
Using a calculator, we obtain:
$latex \theta \approx 53.13^{\circ}$
Therefore, the angle of vector A with respect to the positive $latex x$-axis is approximately 53.13°.
EXAMPLE 2
What is the angle $latex \theta$ of the vector $latex \vec{B}$ that has components $latex B_{x} = -5$ and $latex B_{y} = 12$?
Solution
We can observe the following information:
- $latex B_{x}=-5$
- $latex B_{y}=12$
Applying the angle formula with these components, we have:
$$\theta = \tan^{-1}\left(\frac{V_{y}}{ V_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{12}{-5}\right)$$
Using a calculator, we obtain:
$latex \theta \approx -67.38^{\circ}$
However, since the vector is in the second quadrant (negative $latex x$, positive $latex y$), we must add 180° to the result:
$latex \theta = -67.38^{\circ} + 180^{\circ} $
$latex \theta = 112.62^{\circ}$
Therefore, the angle of vector B with respect to the positive $latex x$-axis is approximately 112.62°.
EXAMPLE 3
Find the angle $latex \theta$ of the vector $latex \vec{C}$ having components $latex C_{x} = -6$ and $latex C_{y} = -8$.
Solution
We can obtain the following information:
- $latex C_{x}=-6$
- $latex C_{y}=-8$
Substituting these values into the formula for the angle of a vector, we have:
$$\theta = \tan^{-1}\left(\frac{C_{y}}{ C_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-8}{-6}\right)$$
Using a calculator, we obtain:
$latex \theta \approx 53.13^{\circ}$
Since the vector is in the third quadrant (negative $latex x$, negative $latex y$), we must add 180° to the result:
$latex \theta = 53.13^{\circ} + 180^{\circ} $
$latex \theta = 233.13^{\circ}$
EXAMPLE 4
What is the angle $latex \theta$ of the vector $latex \vec{D}$ with components $latex D_{x} = 7$ and $latex D_{y} = -3$?
Solution
We can extract the following information:
- $latex D_{x}=7$
- $latex D_{y}=-3$
The angle of the vector is equal to:
$$\theta = \tan^{-1}\left(\frac{D_{y}}{ D_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-3}{7}\right)$$
Using a calculator, we obtain:
$latex \theta \approx -23.2^{\circ}$
Since the vector is in the fourth quadrant ($latex x$ positive, $latex y$ negative), we can add 360° to the result:
$latex \theta = -23.2^{\circ} + 360^{\circ}$
$latex \theta = 336.8^{\circ}$
EXAMPLE 5
If a vector has components $latex A_{x} = -10$ and $latex A_{y} = 0$, what is its angle $latex \theta$?
Solution
In this case, we have a $latex y$ component equal to zero, so using the inverse tangent function, we will obtain an angle equal to zero.
We can solve this problem by considering that the $latex x$ component is negative. Then, we know that the angle formed must be equal to 180°.
$latex \theta =180^{\circ}$
When we have problems similar to this one, it is useful to consider the position on the Cartesian plane axes.
EXAMPLE 6
Find the angle $latex \theta$ of the vector $latex \vec{G}$ with components $latex G_{x} = 8$ and $latex G_{y} = 15$.
Solution
We have the following components:
- $latex G_{x}=8$
- $latex G_{y}=15$
Then, we use the formula for the angle or direction of a vector:
$$\theta = \tan^{-1}\left(\frac{G_{y}}{ G_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{15}{8}\right)$$
Using a calculator, we obtain:
$latex \theta \approx 61.93^{\circ}$
EXAMPLE 7
What is the angle $latex \theta$ of the vector $latex \vec{H}$ with components $latex H_{x} = -12$ and $latex H_{y} = -5$?
Solution
We can observe the following:
- $latex H_{x}=-12$
- $latex H_{y}=-5$
Applying the formula for the angle of a 2D vector, we have:
$$\theta = \tan^{-1}\left(\frac{H_{y}}{ H_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-5}{-12}\right)$$
Using a calculator, we obtain:
$latex \theta \approx 22.62^{\circ}$
Since the vector is in the third quadrant (negative $latex x$, negative $latex y$), we must add 180° to the result:
$latex \theta = 22.62^{\circ} + 180^{\circ}$
$latex \theta = 202.62^{\circ}$
EXAMPLE 8
An airplane is flying on a northerly course at a speed of 150 km/h. There is a strong westerly wind pushing the airplane eastward with a speed of 40 km/h. What is the direction of the airplane relative to the ground?
Solution
Let’s represent the airplane speed with $latex \vec{A}$ to the wind speed with $latex \vec{V}$.
Since the plane is flying north, its velocity components are $latex A_{x}$ = 0$ km/h and $latex A_{y} = 150$ km/h. The wind is blowing from the west, so its velocity components are $latex V_{x} = 40$ km/h and $latex V_{y} = 0$ km/h.
To find the actual velocity and direction of the airplane with respect to the ground, $latex \vec{R}$, we have to add the components of the airplane velocity and the components of the wind velocity:
$latex R_{x} = A_{x} + V_{x} = 0 + 40 = 40$ km/h
$latex R_{y} = R_{y} + V_{y} = 150 + 0 = 150$ km/h
Now, we use the angle formula with these components:
$$\theta = \tan^{-1}\left(\frac{R_{y}}{ R_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{150}{40}\right)$$
$latex \theta \approx 75.62^{\circ}$
Since the angle is measured from the positive $latex x$ axis (east), the aircraft flies approximately 75.96° north of east.
2D Vector direction – Practice problems
Find the angle θ of a vector that has the components $latex V_{x}=0$ and $latex V_{y}=-14$.
Write the angle in degrees.
See also
Interested in learning more about vectors? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
