Uniform Rectilinear Motion, or URM, is a type of motion where an object moves in a straight line at a constant speed. In other words, the object doesn’t speed up or slow down during its journey. It’s like a car traveling down a highway at a steady pace without hitting the brakes or stepping on the gas.
In this article, we will explore a series of Uniform Rectilinear Motion exercises designed to challenge and enhance students’ understanding of this topic.
10 Solved Exercises on Uniform Linear Motion
If you need to review the equations of uniform rectilinear motion, you can visit this article.
EXERCISE 1
An airplane takes 210 minutes to fly directly from city A to city B, maintaining a constant speed of 830 km/h. What distance, in kilometers, separates the two cities?
Solution
Since the airplane flies directly in a straight line from A to B, and maintains its velocity constant, the equation of uniform rectilinear motion is applicable in this case:
$$ x(t)=x_0 + v\cdot t$$
The initial position is $latex x_0 =0$, the speed of the plane is $latex v=830\hspace{1 mm}\frac{km}{h}$ and the time is $latex t=210\hspace{1mm} minutes$. Before substituting the values in the formula, it is necessary to express the time in hours, since the distance that separates the cities in kilometers is requested. Therefore:
$$210\hspace {1 mm}minutes=210\times \frac{1\hspace{1mm} hours}{60\hspace{1 mm} minutes}=3.5\hspace{1 mm}hours$$
Then:
$$ x(t)=v\cdot t$$
$$ x(3.5)=830\hspace{1 mm}\frac{km}{h}\times 3.5\hspace{1 mm}h=2905\hspace{1mm}km$$
The distance between cities A and B is $latex 2905\hspace{1mm}km$.
EXERCISE 2
Geologists have determined that the North American and European continents are moving apart at an estimated rate of about 3 cm/year. If this rate remains constant, how many millions of years will it take for them to move 500 km farther apart than they are today?
Solution
We will assume, for simplicity, that the motion of the continents is uniform rectilinear. Now, we can use the equation:
$$ x(t)=x_0 + v\cdot t$$
And we want:
$$\Delta x = x-x_0$$
Whose value, according to the statement, is:
$$\Delta x = x-x_0=500\hspace{1mm}km$$
$$\Delta x = v\cdot t$$
Solving for the time $latex t$:
$$t=\frac{\Delta x}{v}$$
Before substituting, we need to verify that the units are homogeneous. Kilometers can be expressed in centimeters, or centimeters in kilometers, using scientific notation.
In any case, the time will be in years:
$$t=\frac{\Delta x}{v}=\frac{5\times 10^7\hspace{1mm}cm}{3\hspace{1mm}\dfrac{cm}{year}}=1.7\times 10^7\hspace{1mm}years$$
One million years is $latex 1\times 10^6\hspace{1mm}years$, so the continents will have separated 500 km after about 17 million years.
EXERCISE 3
An object moves with constant speed of 10 m/s in the negative direction of the x-axis. If it is initially at position x=4 m, what will be its position after t=5 seconds?
Solution
Starting from the equation:
$$ x(t)=x_0 + v\cdot t$$
The values $latex x_0= 4\hspace{1mm}m$, $latex v = -10\hspace{1mm}m/s$ and $latex t= 5\hspace{1mm} s$ are taken and these values are substituted to obtain the equation for the position.
The negative sign in the velocity is due to the fact that the object is moving in a negative direction, according to the statement:
$$ x(t)=4 -10\cdot t$$
After t=5 s, the object will be in:
$$ x(5)=4\hspace{1mm}m – \left(10\hspace{1mm}\frac{m}{s}\times5\hspace{1mm} s\right)=-46\hspace{1mm}m$$
Therefore, after t=5 s, the object will be in:
$$ x(5)=-46\hspace{1mm}m$$
EXERCISE 4
The Sun and the Earth are 150 million kilometers apart. Knowing that light moves at constant speed of magnitude $latex 3\cdot 10^8 m/s$, calculate the time it takes light to travel from the Sun to the Earth.
Solution
Starting from the equation for uniform rectilinear motion, solve for the time:
$$ x(t)=v\cdot t\Rightarrow t=\frac{x}{v}$$
Before substituting numerical values in the statement, we need to make sure that the units match, so we can use the speed of light as $latex c=300,000\hspace{1 mm}km/s$, so that time calculated is in seconds:
$$ t=\frac{x}{v}=\frac{150000000\hspace{1 mm}km}{300000\hspace{1mm}\dfrac{km}{s}}=500 \hspace{1mm}s=8.33\hspace{1 mm} minutos$$
The light we see from the Sun took approximately 8 minutes to reach the Earth.
EXERCISE 5
At the start, a particle is at position x=4 m, moving with constant speed along the x-axis, at a rate of v= 8 m/s. Determine:
a) The equation of the position as a function of time.
b) The time it takes to reach the position x = 12 m.
c) Its position after 5 seconds.
d) Its displacement after 5 seconds.
Solution
a) According to the information in the statement, the initial position of the particle is $latex x_0=4\hspace{1mm}m$, and since we know its speed, when substituting values in the equation of motion, it results:
$$x(t)=4+8t$$
b) To calculate the time, we substitute $latex x(t)=12\hspace{1mm}m$ and solve for the time:
$$t=\dfrac{12\hspace{1mm}m-4\hspace{1mm}m}{8\hspace{1mm}m/s}=1\hspace{1mm}s$$
c) After 5 seconds, the particle will be at the position $latex x(5)$, given by:
$$x(5)=4\hspace{1mm}m+\left(8\hspace{1mm}\frac{m}{s}\times 5\hspace{1mm}s\right)=44\hspace{1mm}m$$
d) The displacement in $latex t=5\hspace{1mm}s$ is:
$$\Delta x= x_{final} -x_{initial} =44\hspace{1mm}m- 4\hspace{1mm}m=40\hspace{1mm}m$$
EXERCISE 6
Two cars are moving in uniform rectilinear motion at t=0, with different speeds. Car 1 has a speed of 75 km/h, while car 2 has a speed of 90 km/h. How far will they be from each other after 120 minutes, if:
a) Both cars started from the same point and are moving in the same direction.
b) If they started from the same point and move in opposite directions.
Solution
a) The first step is to convert from minutes to hours:
$$120\hspace{1 mm}minutes=2\hspace{1 mm}hours$$
Since the starting point is the same, $latex x_0=0$ is taken for the two cars.
We will call car 1 the slowest and car 2 the fastest. In that case, car 2 overtakes car 1:
$$x_1=75\frac{km}{h}\times2\hspace{1 mm}hours=150\hspace{1 mm}km$$
$$x_2=90\frac{km}{h}\times2\hspace{1 mm}hours=180\hspace{1 mm}km$$
Therefore, after $latex t=2\hspace{1mm} hours$, the cars are separated by a distance of:
$$ (180 – 150) \hspace{1 mm}km=30 \hspace{1 mm}km$$
b) In this case, to distinguish the directions in which the cars move, it is enough to assign a negative speed to one of them. For example, you can make $latex v_2=-90\hspace{1mm}\frac{km}{h}$. This way:
$$x_1=75\frac{km}{h}\times2\hspace{1 mm}hours=150\hspace{1 mm}km$$
$$x_2=-90\frac{km}{h}\times2\hspace{1 mm}hours=-180\hspace{1 mm}km$$
After $latex t=2\hspace{1mm} hours$, the cars, which have been moving away from each other since the beginning, will be separated by a distance of:
$$ [150-(-180)] \hspace{1 mm}km=330 \hspace{1 mm}km$$
EXERCISE 7
In the following graph $latex x$ position versus $latex t$ time, the motion of a car is shown:
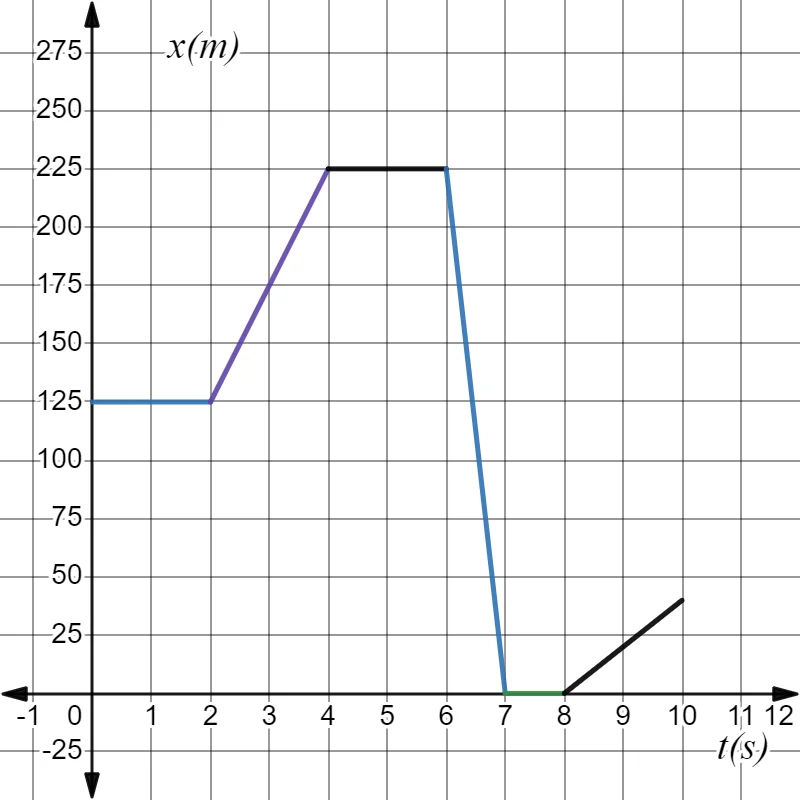
From it, calculate the following:
a) Initial position of the car.
b) Time intervals in which it is stopped.
c) In what time interval does the mobile have negative velocity?
d) And, in which ones does it have positive velocity?
e) The total distance traveled by the car.
f) The speed in each section of the movement.
g) The average speed of the mobile.
Solution
a) The car is initially 125 m from the origin:
$$x_0=125\hspace{1mm}m$$
b) The car is stopped at the following time intervals:
- From $latex t=0$ to $latex t = 2\hspace{1 mm} s$
- From $latex t=4$ to $latex t = 6\hspace{1 mm} s$
- From $latex t=7$ to $latex t = 2\hspace{1 mm} s$
c) The car has negative velocity in the interval:
- From $latex t=6$ to $latex t = 7\hspace{1 mm} s$
d) The car has positive velocity in the interval:
- From $latex t=2$ to $latex t = 4\hspace{1 mm} s$
- From $latex t=8$ to $latex t = 10\hspace{1 mm} s$
e) The total distance is calculated by adding the distances that the car travels in the corresponding time interval:
- From $latex t=0$ to $latex t = 2\hspace{1 mm} s$ it’s at rest, so, $latex \Delta x_1=0\hspace{1mm}m$
- From $latex t=2$ to $latex t = 4\hspace{1 mm} s$ moves $latex \Delta x_2=225-125\hspace{1mm}m=100\hspace{1 mm}m$
- From $latex t=4$ to $latex t = 6\hspace{1 mm} s$ it’s at rest, so, $latex \Delta x_3=0\hspace{1mm}m$
- From $latex t=6$ to $latex t = 7\hspace{1 mm} s$ the car returns to the origin, $latex \Delta x_4=225\hspace{1mm}m$
- From $latex t=7$ to $latex t = 8\hspace{1 mm} s$ it’s at rest, so, $latex \Delta x_5=0\hspace{1mm}m$
- From $latex t=8$ to $latex t = 10\hspace{1 mm} s$ moves $latex \Delta x_6=37.5\hspace{1mm}m$
$$Total ~Distance\hspace{1mm} = 100\hspace{1 mm}m+225\hspace{1mm}m+37.5\hspace{1mm}m=362.5\hspace{1mm}m$$
f) The movement consists of six different sections, in sections 1, 3 and 5 it is at rest, in sections 2 and 6 it has positive speed and in section 4 it has negative speed. The speed is equivalent to the slope of the straight line in each section:
- $latex v_1=0\hspace{1mm}m/s$
- $latex v_2=\dfrac{225m-125m}{4s-2s}=+50\hspace{1mm}m/s$
- $latex v_3=0\hspace{1mm}m/s$
- $latex v_4=\dfrac{225m-0m}{6s-7s}=-225\hspace{1mm}m/s$
- $latex v_5=0\hspace{1mm}m/s$
- $latex v_6=\dfrac{37.5m-0m}{10s-8s}=+18.75\hspace{1mm}m/s$
g) The average speed is the quotient between the total distance traveled and the time the movement lasts:
$$v_m=\dfrac{362.5\hspace{1mm}m}{10\hspace{1mm}s}=36.25\hspace{1mm}m/s$$
EXERCISE 8
Two objects are in uniform rectilinear motion, moving towards each other. At a certain instant, it is observed that they are separated by a distance of 150 m, being their respective opposite velocities 6 m/s and 9 m/s.
a) How long does it take for them to run into each other?
b) What distance separates them after 15 seconds from the initial instant?
Solution
a) Let the initial time be $latex t_0 =0$. At that moment, object 1 is assigned the position $latex x_1=0$ and object 2 is assigned the position $latex x_2 =150\hspace{1mm}m$. Their respective speeds are: $latex v_1=+6\hspace{1mm}m/s$ and $latex v_2=-9\hspace{1mm}m/s$, therefore:
$$x_1(t)=6t$$
$$x_2(t)=150-9t$$
In order to determine the time when they run into each other, the respective equations are equated:
$$6t=150-9t$$
$$15t=150$$
$$t=10\hspace{1mm}s$$
The objects intersect after $latex t = 10\hspace{1mm}s$.
b) After 15 seconds from the initial instant, 5 seconds have passed after they crossed each other. In that time, object 1 traveled the following distance.
$$x_1 = 6t=6 \hspace{1 mm}\frac{m}{s}\times 5\hspace{1mm} s=30 \hspace{1mm}m$$
And the object traveled this other distance:
$$x_2=6t=9 \hspace{1 mm}\frac{m}{s}\times 5\hspace{1mm} s=45\hspace{1mm}m$$
Remember that the distance is always positive, only that the objects move in opposite directions, therefore, the distance that separates them 15 seconds after they have intersected is:
$$30\hspace{1mm}m+45\hspace{1mm}m =75 \hspace{1mm}m$$
EXERCISE 9
Two cars travel in perpendicular directions, under uniform rectilinear motion. If the first vehicle has a constant speed of 12 m/s and the second has a constant speed of 18 m/s, at what moment after crossing each other at the intersection will they be 900 m apart?
Solution
Suppose the red car travels at 12 km/h and the green car travels at 18 km/h. Since they move perpendicularly, their straight trajectories form the sides of a right triangle, while the distance separating them is the hypotenuse.
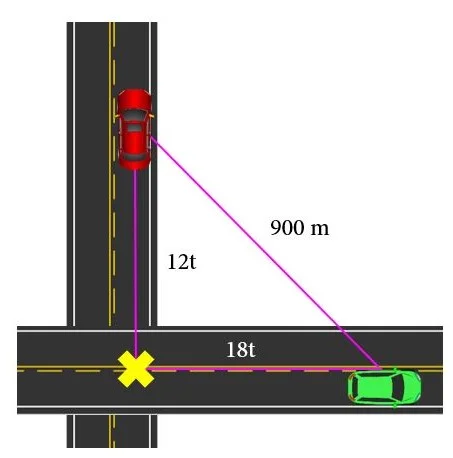
From the Pythagorean theorem:
$$ (18t)^2+(12t)^2 = 900^2 \rightarrow 324t^2+144t^2=810000$$
$$468t^2=810000$$
$$t=\sqrt{\dfrac{810000}{468}}\hspace{1mm}s=41.6\hspace{1mm} s$$
After 41.6 s after the crossing, the cars will be 900 m apart.
EXERCISE 10
A particle moves for 10 seconds on a straight line with a constant speed of 2 m/s, starting from the position x = -8 m, remains at rest for 4 seconds and then moves in the opposite direction for 11 more seconds, with a constant speed of 5 m/s.
a) Write the position function of the particle $latex x(t)$.
b) Construct the graph of the position as a function of time.
c) Where is the particle located at t =18 s?
d) At what position did the particle end up?
e) Construct the graph of velocity as a function of time.
f) From the velocity versus time graph, what distance did the particle travel during the first 20 seconds of its motion?
g) What was the total distance traveled?
h) What was its average speed?
Solution
a) The particle position function is a piecewise function with three sections.
Part 1
Initial position: $latex x_0=-8\hspace{1mm}m$
Duration: starts at $latex t=0$ and ends at $latex t=10\hspace{1mm}s$
Velocity: $latex + 2m/s$
Equation: $latex x(t)=-8+2t$
Final position: $latex x(10)=-8+2\times 10\hspace{1mm} m= 12 \hspace{1mm} m$.
Part 2
Initial position: $latex x(10)=12\hspace{1mm}m$
Duration: starts at $latex t=10\hspace{1mm}s$ and ends at $latex t=16\hspace{1mm}s$
Speed: null
Equation: $latex x(t)= 12\hspace{1mm}m$ (The particle remained at rest)
Final position: $latex x(16)=12\hspace{1mm}m$.
Part 3
Initial position: $latex x(16)=12\hspace{1mm}m$
Duration: starts at $latex t=16\hspace{1mm}s$ and ends at $latex t=25\hspace{1mm}s$
Velocity: $latex v=-5\hspace{1mm}m/s$
Equation: $latex x(t)=12-5(t-16)$ (The time is counted from t=0 and this section began 16 seconds after the movement began, so we must subtract 16 from the variable).
Final position: $latex x(25)=12-5\times (25-16)\hspace{1mm}=-33\hspace{1mm}m$
Putting the three expressions together:
$$x(t) = \left\{\begin{array}{rl} -8+2t & \text{if } 0 \leq t\leq10\\ 12 & \text{if } 10 \leq t\leq16\\ 12-5(t-16) & \text{if } 16\leq t\leq25\end{array} \right. $$
b) Graph of position as a function of time:
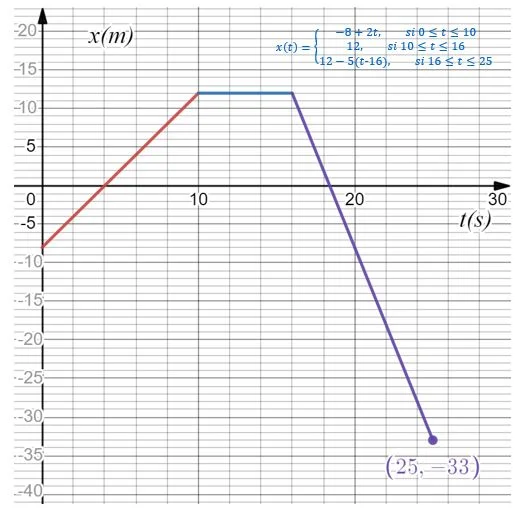
c) At $latex t=18\hspace{1mm}s$ the particle is in $latex x=2\hspace{1mm}m$.
d) At the end of the movement, the particle was in the position $latex x=-33\hspace{1mm}m$.
e) Graph of velocity as a function of time:
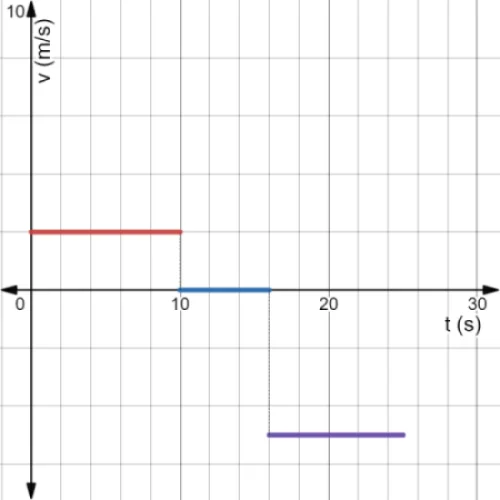
f) The distance traveled during the first 20 seconds is numerically equivalent to the area between the graph and the horizontal axis.
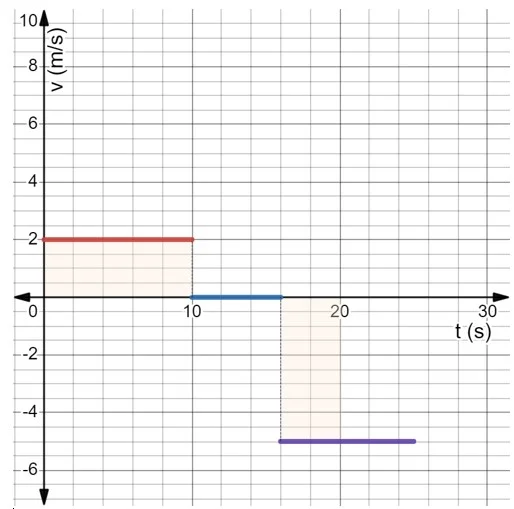
As they are rectangles, the area is calculated by multiplying base by height:
$$d_{20}= |10\hspace{1mm}\times2\hspace{1mm}m/s|+|{4\hspace{1mm}\times(-5\hspace{1mm}m/s)}|=40\hspace{1mm}m$$
Note that the area is always a positive quantity.
g) The total distance traveled by the object is numerically equivalent to the area highlighted in color in the figure.
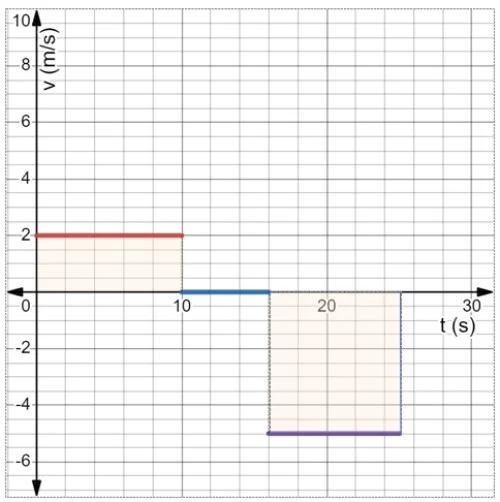
You can use the result of the previous item and add the missing area, which is the area of the rectangle whose base goes from 20s to 25s:
$$d_{25}=40\hspace{1mm}m +|{5\hspace{1mm}s\hspace{1mm}\times(-5\hspace{1mm}m/s)}|=65\hspace{1mm}m$$.
h) The average speed of the trip is calculated by dividing the total distance traveled by the time taken:
$$v_m=\dfrac{65\hspace{1mm}m}{10\hspace{1mm}s}=6.5\hspace{1mm}m/s$$
Uniform rectilinear motion – Practice problems


Write the answer in the input box.
See also
Interested in learning more about motion in physics? You can take a look at these pages:




