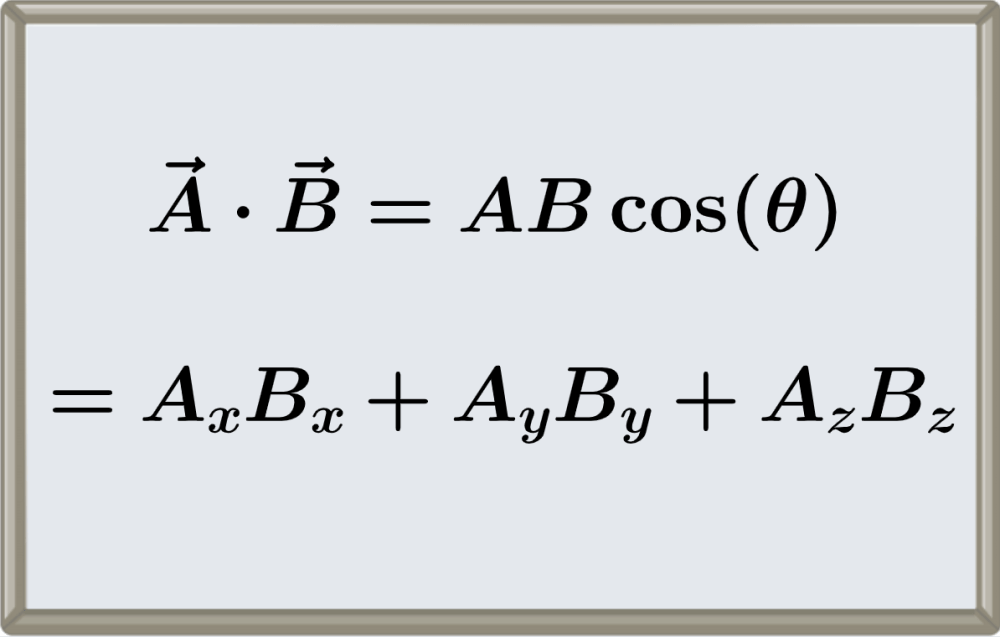Dot Product of Vectors – Examples and Practice

We have the following information:

• $latex |A|=5$
• $latex |B|=3$
• $latex \theta=45^{\circ}$

To find the dot product using magnitudes and the angle, we can use the following formula:

$latex \vec{A} \cdot \vec{B} = |A| ~|B| \cos(\theta)$

$latex = 5 \times 3 \cos(45^{\circ}) $

$$= 15 \left(\frac{\sqrt{2}}{2}\right) $$

$$\approx 10.61$$

We can observe the following:

• $latex |C|=4$
• $latex |D|=6$
• $latex \theta=120^{\circ}$

Use the same formula as in the previous exercise to find the dot product:

$latex \vec{C} \cdot \vec{D} = |C| ~|D| \cos(\theta)$

$latex = 4 \times 6 \cos(120^{\circ}) $

$$= 24 \left(-\frac{1}{2}\right) $$

$$= -12$$

We can observe the following:

• $latex |E|=7$
• $latex |F|=2$
• $latex \theta=90^{\circ}$

Since the angle between vectors E and F is 90°, cos(90°) = 0, so the dot product will be zero:

$latex \vec{E} \cdot \vec{F} = |E| ~|F| \cos(\theta)$

$latex = 7 \times 2 \cos(90^{\circ}) $

$$= 14 \left(0\right) $$

$$= 0$$

The scalar product (dot product) of two vectors A and B can be found with the following formula:

$latex \vec{A} \cdot \vec{B} = A_{x} \times B_{x} + A_{y} \times B_{y} + A_z \times B_{z}$

where $latex A_{x},~ A_{y},~ A_{z}$ are the components of vector $latex \vec{A}$, and $latex B_{x},~ B_{y},~ B_{z}$ are the components of vector $latex \vec{B}$.

Then, the dot product of $latex \vec{A}$ and $latex \vec{B}$ is:

$latex \vec{A} \cdot \vec{B} = (2 \times -1) + (3 \times 4) + (1 \times 2)$

$latex = -2 + 12 + 2 = 12$

We apply the same formula as in the previous example. Then, we have:

$latex \vec{A} \cdot \vec{B} = A_{x} \times B_{x} + A_{y} \times B_{y} + A_z \times B_{z}$

$latex \vec{A} \cdot \vec{B} = (5 \times -3) + (4 \times 0) + (2 \times 3)$

$latex = -15 + 0 + 6$

$latex = -9$

We apply the dot product formula of two vectors using the given components:

$latex \vec{C} \cdot \vec{D} = C_{x} \times D_{x} + C_{y} \times D_{y} + C_z \times D_{z}$

$latex C \cdot D = (4 \times 1) + (-5 \times 2) + (6 \times 3)$

$latex = 4 – 10 + 18 $

$latex = 12$

To find the scalar product of two vectors $latex \vec{E}$ and $latex \vec{F}$ using their components, we can use the following formula:

$latex \vec{E} \cdot \vec{F} = E_{x} \times F_{x} + E_{y} \times F_{y} + E_z \times F_{z}$

$latex \vec{E} \cdot \vec{F} = (-3 \times 5) + (7 \times 2) + (1 \times 4)$

$latex = -15 + 14 + 4 $

$latex = 3$

We can find the scalar product of the vectors as follows:

$latex \vec{G} \cdot \vec{H} = G_{x} \times H_{x} + G_{y} \times H_{y} + G_z \times H_{z}$

$latex \vec{G} \cdot \vec{H} = (3 \times 1) + (-2 \times 2) + (4 \times -2)$

$latex = 3 – 4 – 8$

$latex = -9$

We apply the scalar product formula of two vectors using the components:

$latex \vec{I} \cdot \vec{J} = I_{x} \times J_{x} + I_{y} \times J_{y} + I_z \times J_{z}$

$latex \vec{I} \cdot \vec{J} = (7 \times -2) + (1 \times 6) + (-3 \times 5)$

$latex = -14 + 6 – 15$

$latex = -23$

To find the angle θ between two vectors C and D, we can use the following formula:

$$\cos(\theta) = \frac{\vec{C} \cdot \vec{D}}{ |C|~|D|}$$

where $latex \vec{C} \cdot \vec{D}$ is the dot product of $latex \vec{C}$ and $latex \vec{D}$, and |C| and |D| are the magnitudes of the vectors.

First, we find the dot product:

$latex \vec{C} \cdot \vec{D} = (1 \times 0) + (1 \times -1) + (0 \times 1) = -1$

Now, we find the magnitudes:

$latex |C| = \sqrt{1^2 + 1^2 + 0^2} = \sqrt{2}$

$latex |D| = \sqrt{0^2 + (-1)^2 + 1^2} = \sqrt{2}$

Then, we calculate cos(θ):

$$\cos(\theta) = \frac{-1}{\sqrt{2} \times \sqrt{2}}$$

$$ = -\frac{1}{2}$$

Finally, we find the angle θ:

$latex \theta = \text{arccos}(-\frac{1}{2}) \approx 120^{\circ}$