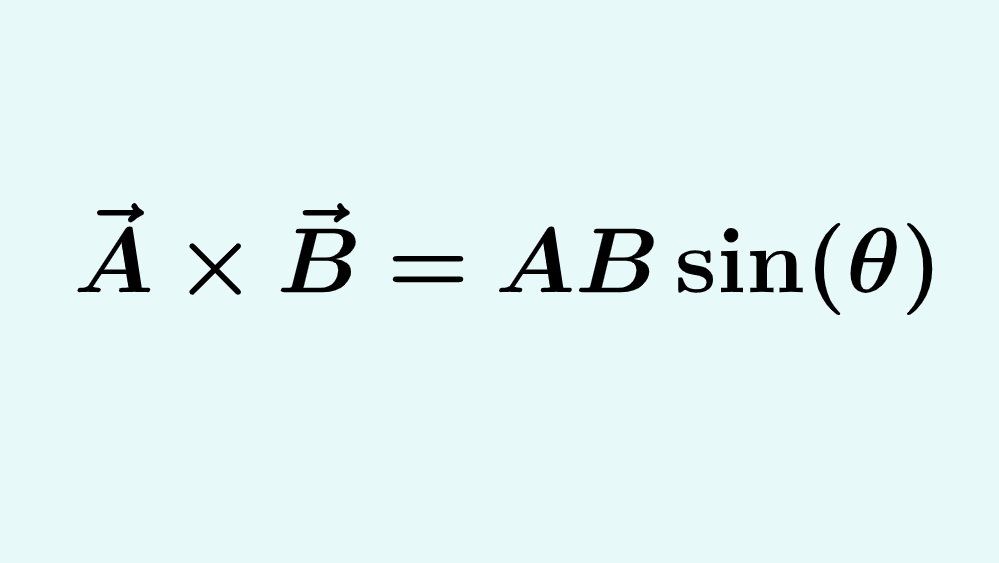The vector product, or cross product of two vectors, can be calculated using two main methods. We can use the magnitudes of the vectors and the angle between their directions. Alternatively, we can use the components of both vectors.
In this article, we will look at several exercises in which we will apply these two methods. Then, we will see some practice problems.
10 Solved examples on cross product of vectors
EXAMPLE 1
We have a vector $latex \vec{A}$ with a magnitude of 8 units in the direction of the $latex +x$ axis. The vector $latex \vec{B}$ has a magnitude of 6 units and is in the $latex x-y$ plane forming an angle of 30° with the $latex +x$ axis.
Find the cross product $latex \vec{C}=\vec{A}\times \vec{B}$.
Solution
We have the following information:
- Magnitude of $latex \vec{A}$: $latex ~A=8$
- Magnitude of $latex \vec{B}$: $latex ~B=6$
- Angle between vectors: $latex ~\theta=30^{\circ}$
Then, we can use the following formula to find the magnitude of the vector $latex \vec{C}$:
$latex C=AB\sin(\theta)$
$latex =(8)(6)\sin(30^{\circ})$
$latex =24$
To find the direction of vector $latex \vec{C}$, we use the following diagram and the right-hand rule:
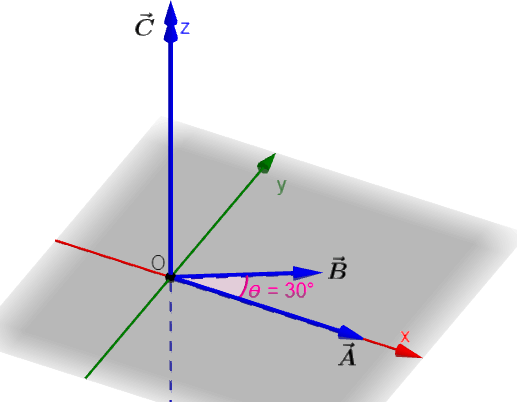
By the right-hand rule, the direction of $latex \vec{A}\times \vec{B}$ is along $latex +z$ or in the direction $latex \hat{k}$. Then,
$latex \vec{C}=\vec{A}\times \vec{B}=24\hat{k}$
EXAMPLE 2
Find the cross product $latex \vec{A} \times \vec{B}$ of the following vectors:
$latex \vec{A} = 2 \hat{i} -3 \hat{j} +4 \hat{k}$
$latex \vec{B} = 1 \hat{i} +5 \hat{j} -2 \hat{k}$
Solution
In this case, we know the components of both vectors. Then, we can find the components of the cross product using the following formula:
$latex C_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex C_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex C_{z} =A_{x} B_{y} – A_{y} B_{x}$
where $latex \vec{C}=\vec{A} \times \vec{B}$. Then:
$latex \vec{A} \times \vec{B} = ((-3)(-2) – (4)(5))\hat{i} +( (4)(1)-(2)(-2))\hat{j} + ((2) (5) – (-3) (1))\hat{k}$
$latex \vec{A} \times \vec{B}=-14\hat{i} + 8\hat{j} + 13\hat{k}$
EXAMPLE 3
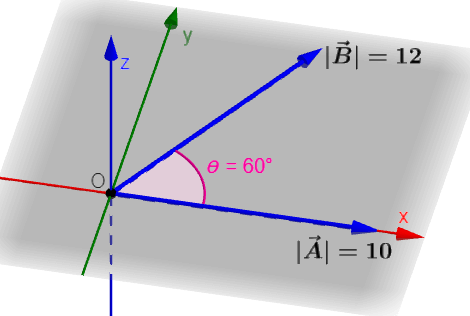
Find the cross product $latex \vec{C}=\vec{A}\times \vec{B}$ of the following vectors:
Solution
We can observe the following:
- Magnitude of $latex \vec{A}$: $latex ~A=10$
- Magnitude of $latex \vec{B}$: $latex ~B=12$
- Angle between vectors: $latex ~\theta=60^{\circ}$
Similar to example 1, we can use the following formula to find the magnitude of vector $latex \vec{C}$:
$latex C=AB\sin(\theta)$
$latex =(10)(12)\sin(60^{\circ})$
$latex =103.92$
Using the given diagram and the right-hand rule, we can determine that the direction of $latex \vec{A}\times \vec{B}$ is $latex \hat{k}$. Then,
$latex \vec{C}=\vec{A}\times \vec{B}=103.92\hat{k}$
EXAMPLE 4
Find the cross product $latex \vec{C} \times \vec{D}$ with the following vectors:
$latex \vec{C} = 3 \hat{i} +0 \hat{j} -7 \hat{k}$
$latex \vec{D} =-4 \hat{i}+ 6 \hat{j} 2 \hat{k}$
Solution
Let’s use the following formulas to find the components of the cross product:
$latex R_{x}=C_{y} D_{z} – C_{z} D_{y}$
$latex R_{y}=C_{z} D_{x}-C_{x} D_{z}$
$latex R_{z} =C_{x} D_{y} – C_{y} D_{x}$
Therefore, we have:
$latex \vec{C} \times \vec{D} = ((0)(2) – (-7)(6)) \hat{i} +((-7)(-4)-(3)(2) )\hat{j} + ((3)(6) – (0)(-4))\hat{k}$
$latex \vec{A} \times \vec{B}=42 \hat{i} +22 \hat{j} +18\hat{k}$
EXAMPLE 5
Find the cross product $latex \vec{A}\times \vec{B}$:
$latex \vec{A} = 5 \hat{i} -2 \hat{j}+ 3\hat{k}$
$latex \vec{B} =1 \hat{i} +4 \hat{j} -1\hat{k}$
Solution
We use the following formulas to find the components of the cross product:
$latex R_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex R_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex R_{z} =A_{x} B_{y} – A_{y} B_{x}$
Then, we have:
$latex \vec{A} \times \vec{B} = ((-2)(-1) – (3)(4)) \hat{i} +((3)(1)-(5)(-1))\hat{j} + ((5)(4) – (-2)(1))\hat{k}$
$latex \vec{A} \times \vec{B}=-10 \hat{i} +8 \hat{j} 22\hat{k}$
EXAMPLE 6
Find the cross product of the following two vectors using their magnitudes and the angle between them:
- Magnitude of vector K: $latex ~|\vec{K}| = 3$
- Magnitude of vector L: $latex ~|\vec{L}| = 4$
- Angle between $latex \vec{K}~$ and $latex ~\vec{L}$: $latex ~\theta= 60^\circ$
Solution
Using the given information, we can apply the cross product formula to find the magnitude of $latex \vec{R}$:
$latex R=KL\sin(\theta)$
$latex =(3)(4)\sin(60^{\circ})$
$latex =12\left(\dfrac{\sqrt{3}}{2}\right)$
$latex = 6\sqrt{3}$
Note that this is only the magnitude; to find the direction of the cross product, we would need the directions of the two given vectors.
EXAMPLE 7
Find the cross product $latex \vec{M}\times \vec{N}$ of the following two vectors:
- Magnitude of vector $latex \vec{M}$: $latex ~|\vec{M}| = 5$
- Magnitude of vector $latex \vec{N}$: $latex ~|\vec{N}| = 7$
- Angle between $latex \vec{M}~$ and $latex ~\vec{M}$: $latex ~\theta= 45^\circ$
Solution
With the given information, we apply the formula for the magnitude of the vector product as follows:
$latex R=MN\sin(\theta)$
$latex =(5)(7)\sin(45^{\circ})$
$latex= 35\left(\dfrac{\sqrt{2}}{2}\right)$
$latex = \dfrac{35\sqrt{2}}{2}$
Similar to the previous example, we need more information about the vectors to determine the direction of the vector product.
EXAMPLE 8
What is the magnitude of vector $latex \vec{R}$ if $latex \vec{R}=\vec{A}\times \vec{B}$?
- Magnitude of vector $latex \vec{A}$: $latex ~|\vec{A}| = 8$
- Magnitude of vector $latex \vec{B}$: $latex ~|\vec{B}| = 6$
- Angle between $latex \vec{A}~$ and $latex ~\vec{B}$: $latex ~\theta= 120^\circ$
Solution
We use the data given in the formula for the magnitude of the cross product:
$latex R=AB\sin(\theta)$
$latex =(8)(6)\sin(120^{\circ})$
$latex= 48\left(\dfrac{\sqrt{3}}{2}\right)$
$latex = 24\sqrt{3}$
To determine the direction of the vector product, we need the directions of the given vectors.
EXAMPLE 9
Find the cross product $latex \vec{A}\times \vec{B}$ using the following vectors:
$latex \vec{A} = 6 \hat{i} -3 \hat{j} +1 \hat{k}$
$latex \vec{B} = 2 \hat{i} +4 \hat{j} -5 \hat{k}$
Solution
Since we know the components of the vectors, we can use the following formulas to find the components of the vector resulting from the cross product:
$latex R_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex R_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex R_{z} =A_{x} B_{y} – A_{y} B_{x}$
Using the given values, we have:
$latex \vec{A} \times \vec{B} = ((-3)(-5) – (1)(4)) \hat{i} +((1)(2)-(6)(-5))\hat{j} + ((6)(4) – (-3)(2))\hat{k}$
$latex \vec{A} \times \vec{B}=11 \hat{i} +32\hat{j} +30\hat{k}$
EXAMPLE 10
We have the vectors $latex \vec{M}=2\hat{i} − 3\hat{j} + \hat{k}~$ and $latex ~\vec{B}= \hat{i} + 2\hat{j} − 3\hat{k}$. Show that $latex \vec{A}\times \vec{B}$ is perpendicular to $latex \vec{A}$ and to $latex \vec{B}$.
Solution
Let’s start by finding the cross product $latex \vec{A}\times \vec{B}$:
$latex \vec{A}\times \vec{B}=((−3)(−3) − (2)(1))\hat{i} + ((1)(1) − (−3)(2))\hat{j} ++((2)(2) − (1)(−3))\hat{k}$
$latex =7\hat{i} +7\hat{j} + 7\hat{k}$
To prove that $latex \vec{A}\times \vec{B}$ is perpendicular to $latex \vec{A}$, we must have $latex (\vec{A}\times \vec{B})\cdot \vec{A}=0$:
$$(\vec{A}\times \vec{B})\cdot \vec{A}=\begin{pmatrix} 7 \\ 7 \\ 7 \end{pmatrix}\cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$$
$latex = 14 − 21 + 7 = 0$
To show that $latex \vec{A}\times \vec{B}$ is perpendicular to $latex \vec{B}$, we must have $latex (\vec{A}\times \vec{B})\cdot \vec{B}=0$:
$$(\vec{A}\times \vec{B})\cdot \vec{B}=\begin{pmatrix} 7 \\ 7 \\ 7 \end{pmatrix}\cdot \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix}$$
$latex = 7+14-21 = 0$
Cross product of vectors – Practice problems
See also
Interested in learning more about vectors? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
