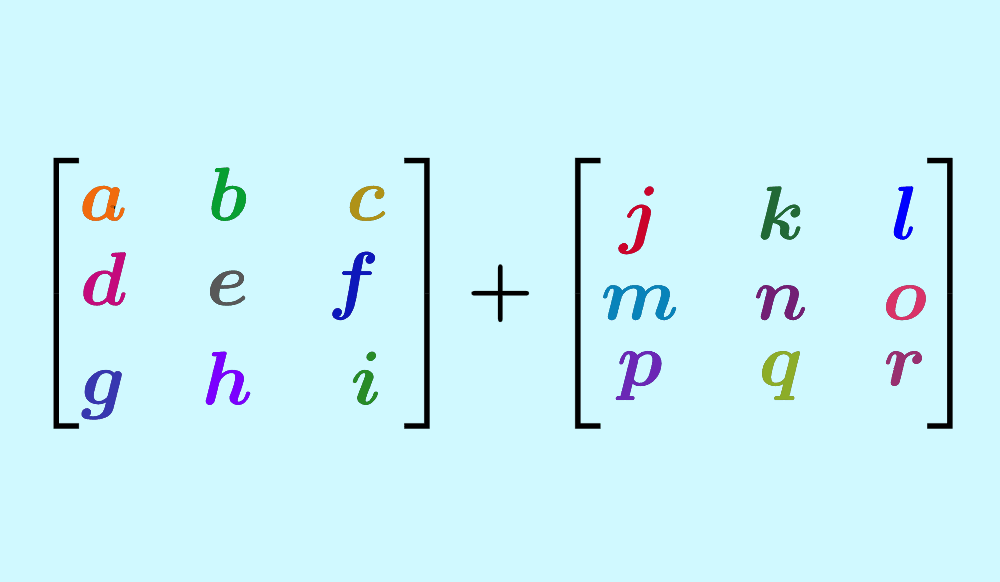Matrices are commonly used in mathematics and other fields to represent data or solve equations. To add and subtract matrices, simply add and subtract the corresponding elements in each position.
In this article, we will learn the steps necessary to add and subtract 3×3 matrices, provide several examples with solutions, and offer practice problems to help you develop your skills.
How to add and subtract 3×3 matrices?
To add and subtract 3×3 matrices we have to add or subtract each corresponding element of two or more matrices of the same size.
We can add or subtract 3×3 matrices by following the steps below:
Step 1: Write the two matrices you want to add side by side with a plus (+) or subtraction (-) symbol between them.
Step 2: Add or subtract each corresponding element of the two arrays.
For example, add the first element of the first array to the first element of the second array, and so on. Write the result to a new array of the same size.
Step 3: Repeat step 2 for each corresponding element until you have added or subtracted all the elements.
For example, suppose we have the following 3×3 matrices:
$$A = \begin{bmatrix} 1& 2 & 3 \\ 7& 8&9 \\ 5& 4&6\end{bmatrix}$$
$$B = \begin{bmatrix} 4& 5 & 6 \\ 2& 3&1 \\ 0& 1&2\end{bmatrix}$$
We add the matrices to obtain A+B:
$$A+B = \begin{bmatrix} 1+4& 2+5 & 3+6 \\ 7+2& 8+3&9+1 \\ 5+0& 4+1&6+2\end{bmatrix}$$
$$A+B = \begin{bmatrix} 5& 7&9\\ 9& 11 & 10 \\ 5& 5 &8\end{bmatrix}$$
We subtract the matrices to obtain A-B
$$A+B = \begin{bmatrix} 1-4& 2-5 & 3-6 \\ 7-2& 8-3&9-1 \\ 5-0& 4-1&6-2\end{bmatrix}$$
$$A+B = \begin{bmatrix} -3& -3&-3\\ 5& 5 & 8 \\ 5& 3 &4\end{bmatrix}$$
Note: Keep in mind that you can only add or subtract matrices of the same size, so in this case, both matrices must be 3×3 matrices.
Solved exercises on addition and subtraction of 3×3 matrices
EXAMPLE 1
What is the addition of the following matrices?
$$ A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$ B= \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} $$
Solution
We can solve this exercise by adding the corresponding elements of both matrices in each position:
$$ A+B= \begin{bmatrix} 1+0 & 2+1 & 3+2 \\ 4+3 & 5+4 & 6+5 \\ 7+6 & 8+7 & 9+8 \end{bmatrix}$$
$$A+B = \begin{bmatrix} 1 & 3 & 5 \\ 7 & 9 & 11 \\ 13 & 15 & 17 \end{bmatrix} $$
EXAMPLE 2
Find the subtraction A-B of the following matrices.
$$ A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$ B= \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} $$
Solution
This example asks us to subtract matrix B from matrix A. Then, we subtract the corresponding elements:
$$ A-B= \begin{bmatrix} 1-0 & 2-1 & 3-2 \\ 4-3 & 5-4 & 6-5 \\ 7-6 & 8-7 & 9-8 \end{bmatrix}$$
$$A-B = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} $$
EXAMPLE 3
Determine the result of the subtraction B-A.
$$ A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$ B= \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} $$
Solution
To solve this exercise, we must consider that the subtraction B-A is not equal to the subtraction A-B. In this case, we subtract matrix A from matrix B:
$$ B-A= \begin{bmatrix} 0-1 & 1-2 & 2-3 \\ 3-4 & 4-5 & 5-6 \\ 6-7 & 7-8 & 8-9 \end{bmatrix}$$
$$B-A = \begin{bmatrix} -1 & -1 & -1 \\ -1 & -1 & -1 \\ -1 & -1 & -1 \end{bmatrix} $$
EXAMPLE 4
What is the result of adding and subtracting (A-B) the following matrices?
$$A = \begin{bmatrix} 6 & 3 & 2 \\ -3 & 5 & 3 \\ -5 & 2 & -9 \end{bmatrix} $$
$$B = \begin{bmatrix} -3 & 7 & 8 \\ 11 & -8 & 5 \\ -5 & 8 & 12 \end{bmatrix} $$
Solution
When we add the matrices, we have:
$$A+B = \begin{bmatrix} 6-3 & 3+7 & 2+8 \\ -3+11 & 5-8 & 3+5 \\ -5-5 & 2+8 & -9+12 \end{bmatrix} $$
$$A+B = \begin{bmatrix} 3 & 10 & 10 \\ 8 & -3 & 2 \\ -10 & 10 & 3 \end{bmatrix} $$
When we subtract the matrices, we have:
$$A-B = \begin{bmatrix} 6+3 & 3-7 & 2-8 \\ -3-11 & 5+8 & 3-5 \\ -5+5 & 2-8 & -9-12 \end{bmatrix} $$
$$A-B = \begin{bmatrix} 9 & -4 & -6 \\ -14 & 13 & -2 \\ 0 & -6 & -21 \end{bmatrix} $$
EXAMPLE 5
Determine the addition and difference B-A of the following matrices.
$$A = \begin{bmatrix} 12 & -13 & 9 \\ -8 & 15 & 13 \\ -6 & -14 & 8 \end{bmatrix} $$
$$A = \begin{bmatrix} 6 & -8 & 12 \\ 11 & 13 & -7 \\ 5 & 12 & -9 \end{bmatrix} $$
Solution
By adding the given matrices A and B, we have:
$$A+B = \begin{bmatrix} 12+6 & -13-8 & 9+12 \\ -8+11 & 15+13 & 13-7 \\ -6+5 & -14+12 & 8-9 \end{bmatrix} $$
$$A+B = \begin{bmatrix} 18 & -21 & 21 \\ 3 & 28 & 6 \\ -1 & -2 & 1 \end{bmatrix} $$
The result of subtraction B-A is
$$B-A = \begin{bmatrix} 6-12 & -8+13 & 12-9 \\ 11+8 & 13-15 & -7-13 \\ 5+6 & 12+14 & -9-8 \end{bmatrix} $$
$$A+B = \begin{bmatrix} -6& 5 & 3 \\ 19 & -2 & -20 \\ 11 & 26 & -17 \end{bmatrix} $$
EXAMPLE 6
If we have the following matrices, what are the values of $latex a$ and $latex b$.
$$A = \begin{bmatrix} 7 & 11 & -12 \\ 9 & 23 & 11 \\ -8 & -6 & a \end{bmatrix} $$
$$B = \begin{bmatrix} 4 & -8 & 7 \\ 14 & b & -7 \\ 5 & 2 & -9 \end{bmatrix} $$
$$A+B = \begin{bmatrix} 11 & 3 & -5 \\ 23 & 11 & 4 \\ 3 & -4 & -2 \end{bmatrix} $$
Solution
In this exercise, we know the sum of the matrices and we have to find the values of $latex a$ and $latex b$.
For this, we can form equations with the addition in each position of the required element:
$latex a+(-9)=-2$
$latex 23+b=11$
Solving the equations, we have:
$latex a=7$
$latex b=-12$
Addition and subtraction of 3×3 matrices – Practice problems
Write the answer in the input box.
See also
Interested in learning more about matrices? You can take a look at these pages:
–
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
