The perimeter of geometric figures is one of the most important measurements of two-dimensional figures. The perimeter measures the total length of the outline of the figure. This means that the perimeter is calculated by adding the lengths of all the sides of the figure. The perimeter can be useful when we want to measure the outline of objects. For example, if we want to build a wire fence, we need to know the perimeter of the region that we are going to fence to know the meters of wire that we will use. Perimeter is a measure that applies to both regular and irregular shapes.
Here, we will learn about the formulas for the perimeter of the most common 2D figures and we will apply them to solve some problems.
GEOMETRY
Relevant for…
Learning about the formulas for the perimeter of geometric figures.
GEOMETRY
Relevant for…
Learning about the formulas for the perimeter of geometric figures.
Definition of perimeter
The perimeter of a geometric figure is defined as the distance around the limits of the figure. To find the perimeter, we need to add the lengths of all the sides of the figure.
Therefore, the formulas for calculating the perimeter of different figures simply depend on the number of sides of the figure. Many times, it is possible to simplify formulas if two or more sides have the same length.
Two geometric figures with different shapes can have the same perimeter depending on the length of their sides or the shape of their contour. For example, a circle and a square can have the same perimeter depending on the sides of the square.
Formulas for the perimeter of geometric figures
The perimeter formulas depend on the number of sides of the figure. Also, when two or more sides have the same length, it is possible to simplify the formula.
Perimeter of a rectangle
A rectangle is characterized by having internal angles of 90°. In a rectangle, its opposite sides are parallel and have the same length.
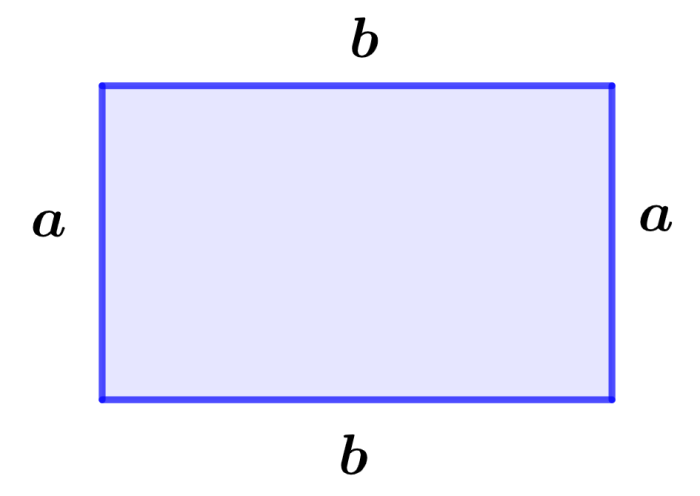
Perimeter of rectangle = 2(a+b)
where a is the length of the width of the rectangle and b is the length of the base.
Perimeter of a square
A square is technically a type of rectangle with the difference that its four sides have the same length.
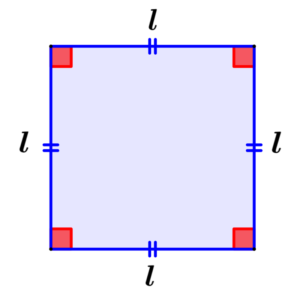
Perimeter of square = 4l
where l represents the length of one of the sides of the square.
Perimeter of a triangle
A triangle is characterized by having three sides. There are three types of triangles depending on the lengths of their sides. A triangle is equilateral if the triangle has all sides of equal length. A triangle is isosceles when it has two equal sides. A triangle is scalene when it has three unequal sides.
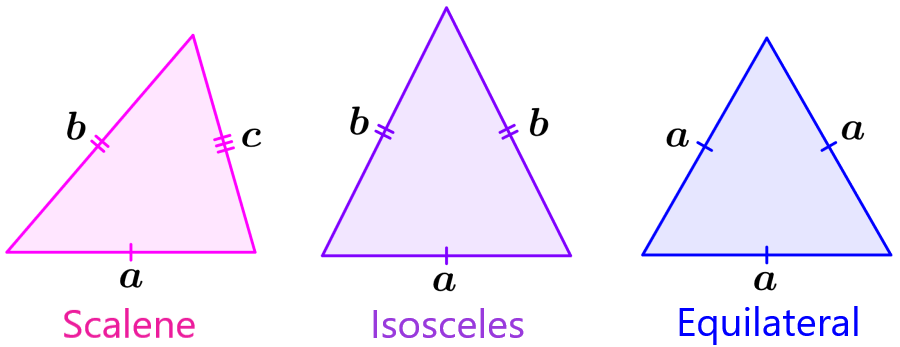
Perimeter of a scalene triangle = a+b+c
Perimeter of an isosceles triangle = a+2b
Perimeter of an equilateral triangle = 3a
where, a, b, c are the lengths of the sides of the triangle.
Perimeter of a circle
The perimeter of a circle is known as the circumference. The perimeter of a circle is calculated using the length of the radius.
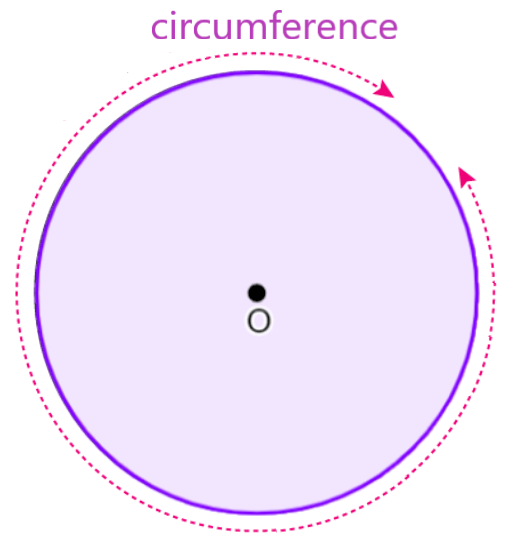
Perimeter of circle = 2πr
where r represents the radius of the circle and π is a mathematical constant that has a value of 3.1415…
Perimeter of regular polygons
A regular polygon is a geometric figure that has all its sides the same length. The perimeter of regular polygons depends on the number of sides of the polygon.
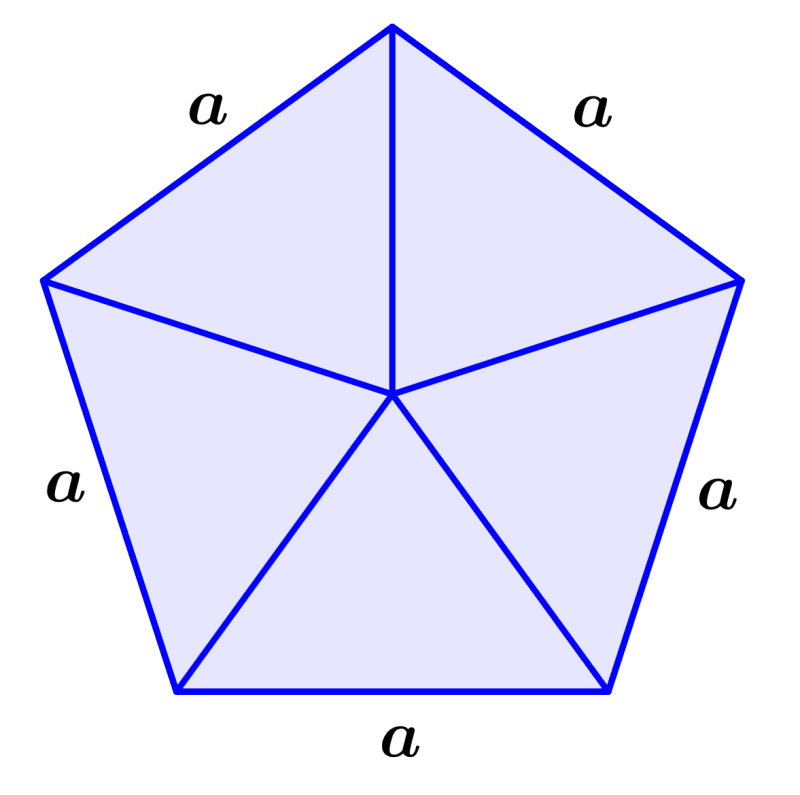
Perimeter of regular polygon = na
where a is the length of one of the sides and n is the number of sides. For example, the formula for the perimeter of a pentagon is 5a since it has five sides.
Table of formulas for the perimeter of geometric figures
| Figure | Perimeter |
| Circle | P = 2πr |
| Scalene triangle | P = a+b+c |
| Isosceles triangle | P = a+2b |
| Equilateral triangle | P = 3a |
| Square | P = 4l |
| Rectangle | P = 2(a+b) |
| Parallelogram | P = 2(a+b) |
| Regular polygon | P = na |
where, r is the radius, a, b, c, l, represent the different lengths of the geometric figures.
Perimeter of geometric figures – Examples with answers
The formulas for the perimeter of various geometric figures are used to solve the following examples. Each example has its respective solution, where you can see the process used.
EXAMPLE 1
A square has sides of length 15 m. What is its perimeter?
Solution
We use the given length in the formula for the perimeter of a square. A square has four equal sides, so we have:
$latex p=4l$
$latex p=4(15)$
$latex p=60$
Therefore, the perimeter of the square is 60 m.
EXAMPLE 2
A circle has a radius of 8 m. What is its perimeter?
Solution
We use the circumference formula to solve this question:
$latex P=2\pi r$
$latex P=2\pi (8)$
$latex P=50.3$
Therefore, the perimeter of the circle is 50.3 m.
EXAMPLE 3
An isosceles triangle has a base 5 m long and two lateral sides 6 m long. What is its perimeter?
Solution
An isosceles triangle has two equal sides, so we use its perimeter formula and we have:
$latex p=a+2b$
$latex p=5+2(6)$
$latex p=5+12$
$latex p=17$
Therefore, the perimeter of the triangle is 17 m.
EXAMPLE 4
What is the perimeter of a rectangle that has sides of length 11 m and 12 m?
Solution
A rectangle has opposite sides that are the same length. Therefore, the perimeter formula is:
$latex p=2(a+b)$
$latex p=2(11+12)$
$latex p=2(23)$
$latex p=46$
The perimeter of the rectangle is 46 m.
EXAMPLE 5
What is the perimeter of a hexagon that has sides of length 6 m?
Solution
A hexagon is a regular polygon with six sides, so the formula for its perimeter is:
$latex P=6a$
$latex P=6(6)$
$latex P=36$
The perimeter of the hexagon is 36 m.
Perimeter of geometric figures – Practice problems
Solve the following practice problems applying the formulas for the perimeter of different geometric figures.
See also
Interested in learning more about geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
