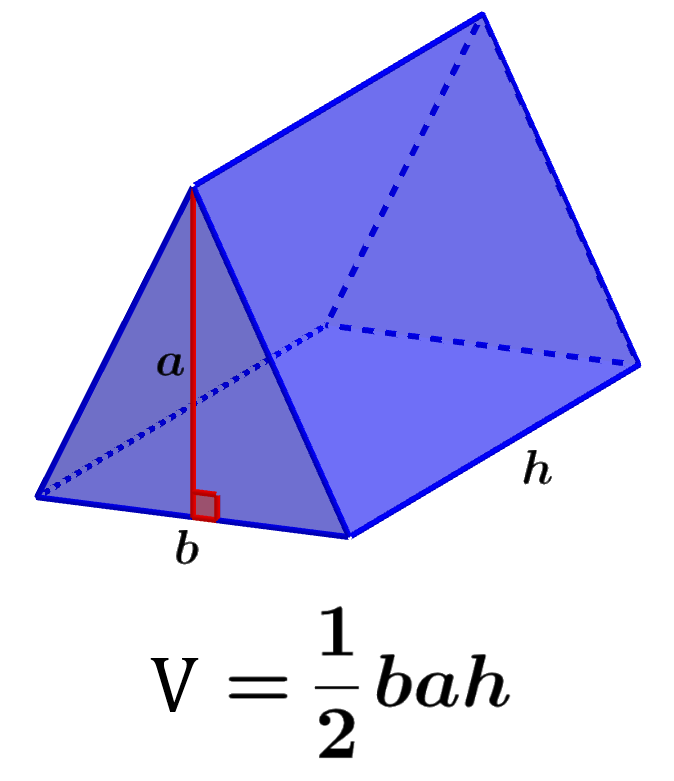
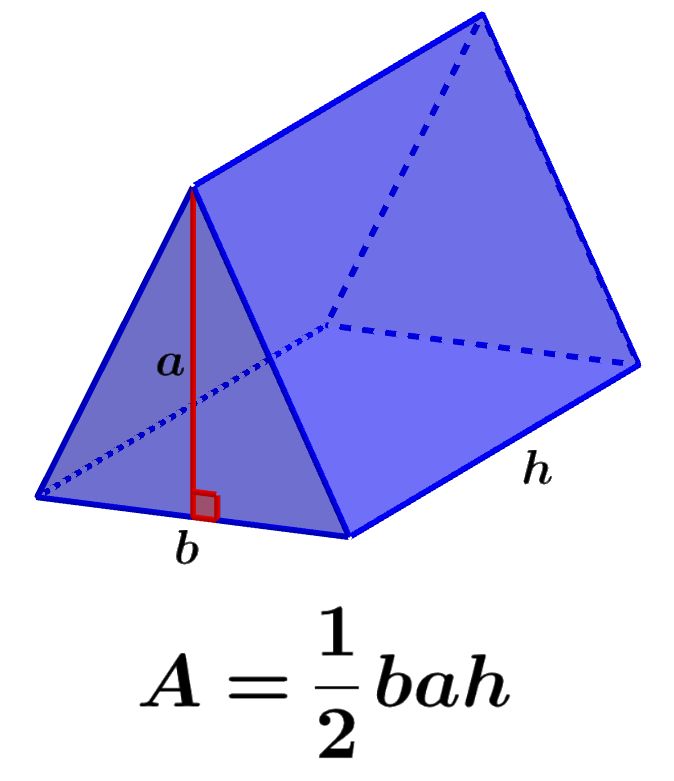
The volume of a triangular prism is the total space occupied by the prism in three-dimensional space. We can calculate the volume of the prism by multiplying the area of the base by the height of the prism. We know that triangular prisms have triangular bases, and we also know that the area of any triangle is calculated by multiplying one-half the length of the base by the length of the height.
Here, we will learn about the formula that we can use to calculate the volume of a rectangular prism. Also, we will use this formula to solve some practice problems.
Formula to find the volume of a triangular prism
The volume of a rectangular prism can be found by multiplying the area of the base times the length of the height of the prism. The base of these prisms is a triangle, so we have to find the area of the triangle.
Recall that the area of any triangle is calculated by multiplying the length of the base by the length of the height by one-half. Therefore, we can use the following formula to calculate the volume of a rectangular prism:
| $latex V=\frac{1}{2}b\times a\times h$ |
where,
- b is the length of the triangle’s base
- a is the length of the height of the triangle
- h is the length of the height of the prism
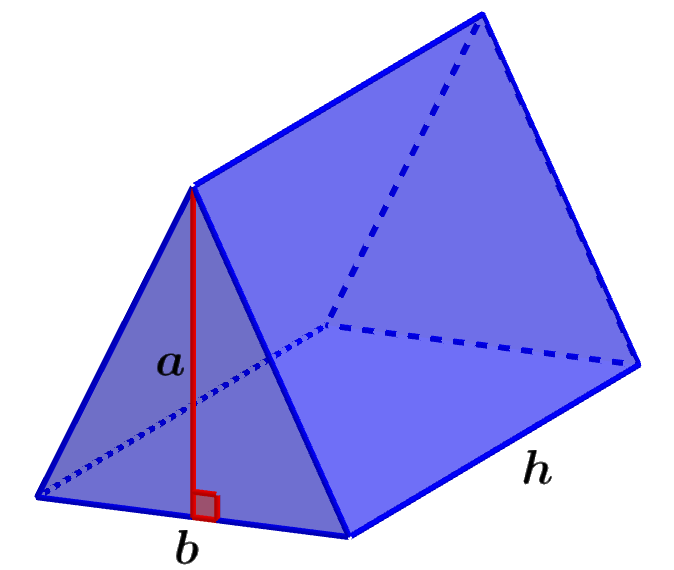
Volume of a triangular prism – Examples with answers
The formula for the volume of triangular prisms is used to solve the following examples. Each example has its respective solution, where the process and reasoning used are detailed.
EXAMPLE 1
A prism has a height of 5 m and its triangular base has a height of 3 m and a base of 4 m. What is its volume?
Solution
We have the following lengths:
- Prism height, $latex h=5$
- Triangle height, $latex a=3$
- Triangle base, $latex b=4$
Using these values in the volume formula, we have:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(4)(3)(5)$
$latex V=30$
The volume is 30 m³.
EXAMPLE 2
What is the volume of a prism that has a height of 6 m and its triangular base has a height of 5 m and a base of 6 m?
Solution
We have the following values:
- Prism height, $latex h=6$
- Triangle height, $latex a=5$
- Triangle base, $latex b=6$
Using the volume formula, we have:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(6)(5)(6)$
$latex V=90$
The volume is 90 m³.
EXAMPLE 3
A prism has a height of 8 m and its triangular base has a height of 6 m and a base of 7 m. What is its volume?
Solution
We have the following lengths:
- Prism height, $latex h=8$
- Triangle height, $latex a=6$
- Triangle base, $latex b=7$
We substitute these values in the volume formula:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(7)(6)(8)$
$latex V=168$
The volume is 168 m³.
EXAMPLE 4
A prism has a height of 11 m and its triangular base has a height of 5 m and a base of 4 m. What is its volume?
Solution
From the question, we get the values:
- Prism height, $latex h=11$
- Triangle height, $latex a=5$
- Triangle base, $latex b=4$
Using these values in the volume formula, we have:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(4)(5)(11)$
$latex V=110$
The volume is 110 m³.
EXAMPLE 5
What is the volume of a prism that has a height of 9 m and its triangular base has a height of 6 m and a base of 8 m?
Solution
We have the following values:
- Prism height, $latex h=9$
- Triangle height, $latex a=6$
- Triangle base, $latex b=8$
Substituting these values in the formula, we have:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(8)(6)(9)$
$latex V=216$
The volume is 216 m³.
Volume of a triangular prism – Practice problems
Practice using the formula for the volume of triangular prisms to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about triangular prisms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
