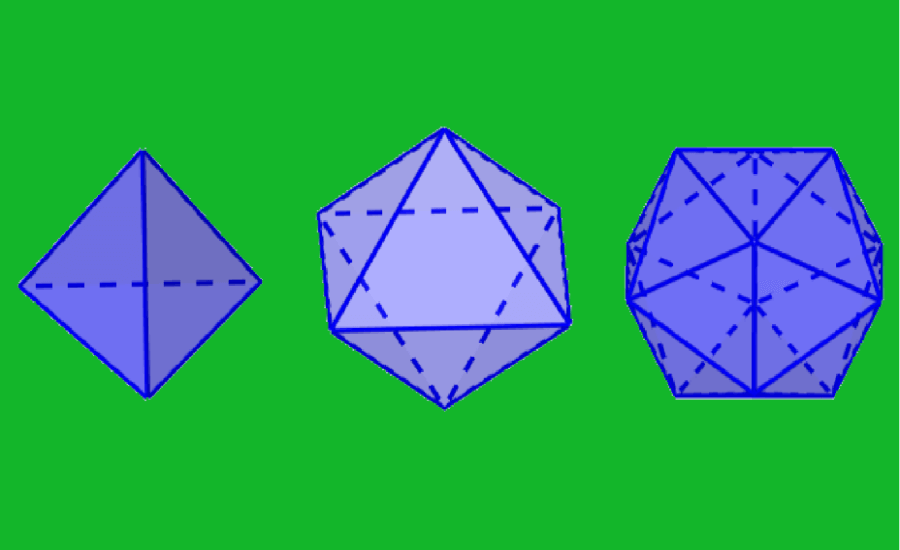
Platonic solids are three-dimensional figures, in which all their faces are congruent regular polygons. In total, there are five Platonic solids: tetrahedron, cube, octahedron, dodecahedron, and icosahedron. These figures are associated with the five elements of nature: fire, earth, air, water, and the universe.
Here, we will learn more details about the five Platonic solids. We will learn about their diagrams and some of their most important properties.
What are Platonic solids?
Platonic solids are regular, convex polyhedra that have congruent faces. This means that a Platonic solid is made up of faces that regular polygons with the same shape and the same size.
Additionally, we can define the Platonic solids as three-dimensional figures, in which all their faces are the same regular polygon and in which the same number of faces meet at each vertex.
In total, there are five geometric figures that meet these conditions, so we have five Platonic solids:
- Tetrahedron
- Cube
- Octahedron
- Dodecahedron
- Icosahedron
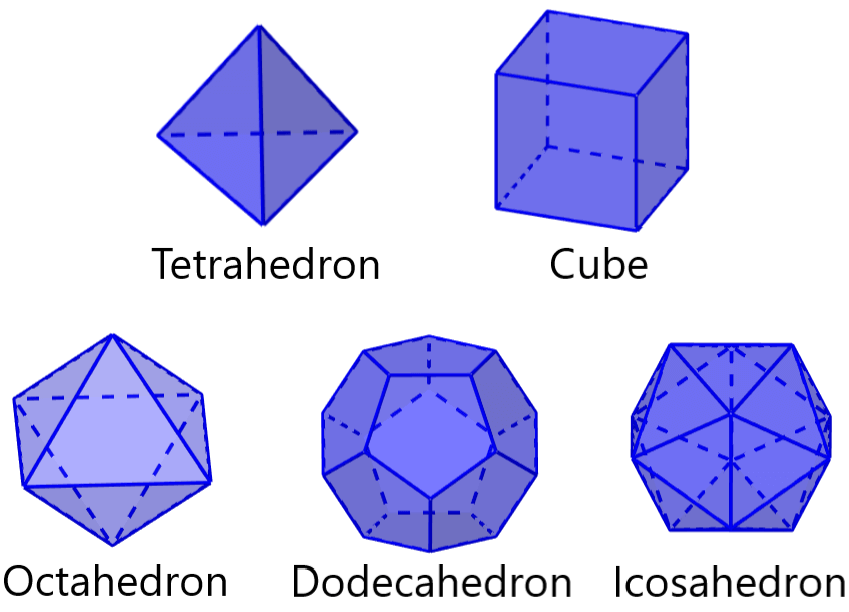
Plato was the one who studied these geometric figures and for this reason, these figures were named Platonic solids. Furthermore, Plato associated each figure with the five elements of nature:
- The tetrahedron with fire
- The cube with the earth
- The octahedron with the air
- The icosahedron with water
- The dodecahedron with the universe
Platonic solids properties
The following are some of the most important properties of Platonic solids:
- Platonic solids are convex polyhedra.
- All faces of the Platonic solids are regular and congruent.
- The same number of faces meet at each vertex.
- Platonic solids comply with Euler’s formula: F+V-E=2, where F is the number of faces, V is the number of vertices, and E is the number of edges.
- The sum of the angles at each vertex is less than 360°.
- All Platonic solids have parallel faces, except for the tetrahedron.
The 5 Platonic solids
The 5 Platonic solids are: tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
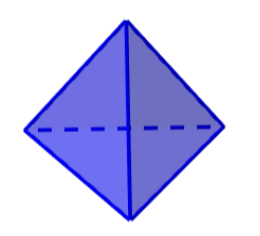
1. Tetrahedron
The tetrahedron is a Platonic solid, which has triangular faces. This figure is also known as a triangular pyramid. The tetrahedron consists of 4 triangular faces, 6 edges, and 4 vertices.
The four vertices of the tetrahedron are at similar distances from each other. Unlike other platonic solids, tetrahedra do not have parallel faces. However, they have 6 planes of symmetry.
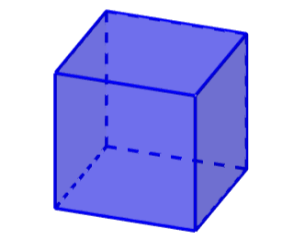
2. Cube
The cube is a Platonic solid, which has square faces. The cube is also known as a regular hexahedron since it has six identical square faces. A cube consists of 6 faces, 12 edges, and 8 vertices.
The opposite faces of a cube are parallel to each other. Each of the faces of the cube meets 4 other faces, one on each of its edges. Also, the angle between two faces is a right angle, that is, 90°.
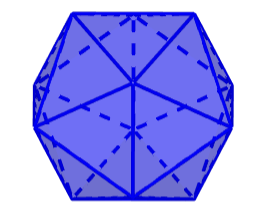
3. Octahedron
The octahedron is a Platonic solid, which has all its faces with a triangular shape. An octahedron has 8 triangular faces, 12 edges, and 6 vertices. These figures have the shape of a double square pyramid.
Each of the faces of the octahedron meets three other faces. Also, four faces meet at each vertex.
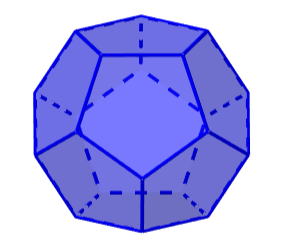
4. Dodecahedron
The dodecahedron is a Platonic solid, which has all its faces with a pentagonal shape. A dodecahedron consists of 12 faces, 30 edges, and 20 vertices. Three pentagonal faces meet at each vertex.
An interesting property of dodecahedrons is that they have 160 diagonals. In addition, these figures can be seen commonly in real life, especially in dodecahedron-shaped dice.
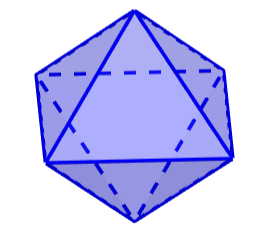
5. Icosahedron
The icosahedron is a Platonic solid, which has all its faces with a triangular shape. Icosahedrons have 20 faces, 30 edges, and 12 vertices.
Icosahedrons are the Platonic solids with the largest number of faces. Furthermore, these figures have the largest volume relative to their surface area.
Why are there only 5 Platonic solids?
For a three-dimensional figure to be a Platonic solid, it must be composed of congruent regular polygons. In turn, for this to be possible, the figure must meet the following conditions:
- At least 3 faces must meet at each vertex of the Platonic solid.
- Interior angles that meet at a vertex must be less than 360°.
The reason for the first condition is that if only two faces meet at each vertex, it is not possible to form a closed three-dimensional figure.
The reason for the second condition is that if the angles formed at a vertex are equal to 360°, the figures would be flat.
Considering this, it turns out that only the 5 figures known as Platonic solids meet these conditions, as we can see in the following table:
| Platonic solid | Each vertex | Angles at vertices |
| Tetrahedron | 3 triangles | Each angle = 90° 90×3=270° |
| Cube | 3 squares | Each angle = 60° 60×3=180° |
| Octahedron | 4 triangles | Each angle = 60° 60×4=240° |
| Dodecahedron | 3 pentagons | Each angle = 108° 108×3=324° |
| Icosahedron | 5 triangles | Each angle = 60° 60×5=300° |
The only figures that can form the Platonic solids are triangles, squares, and pentagons. There are three possible ways we can form a three-dimensional vertex, with equilateral triangles, squares, and pentagons.
Therefore, there are five ways to arrange regular polygons around a vertex to form a net, which can be folded to form a concave three-dimensional figure.
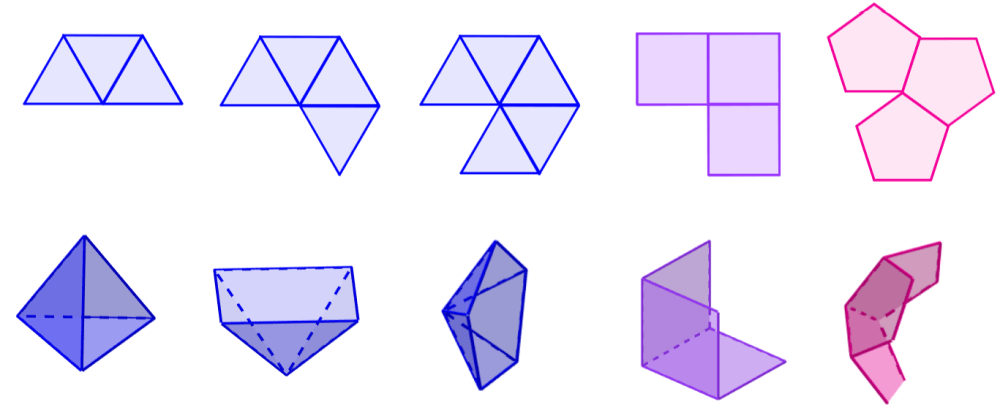
The triangles form the tetrahedrons, octahedrons, and icosahedrons.
The squares form the cubes.
The pentagons form the dodecahedrons.
Examples of Platonic solids
The following examples are solved using basic knowledge of Platonic solids.
EXAMPLE 1
Which of the following is not a Platonic solid?
- Tetrahedron
- Cube
- Hexagon
- Dodecahedron
Solution: The hexagon is not a Platonic solid, since it is a two-dimensional figure. The tetrahedron, the cube, and the dodecahedron are indeed Platonic solids since they meet all the conditions.
EXAMPLE 2
What is the name of the following Platonic solid?

Solution: We can see that the Platonic solid has 12 pentagonal faces, so we know that it is called a dodecahedron.
EXAMPLE 3
A Platonic solid has 20 faces and 12 vertices. How many edges does it have?
Solution: The Platonic solids comply with Euler’s formula. Therefore, by using the formula with the given data, we have:
F+V-E=2
E=F+V-2
E=20+12-2
E=30
So the Platonic solid has 30 edges.
See also
Interested in learning more about Platonic solids and geometric figures? Look at these pages: