The most important elements of the Platonic solids are the faces, the vertices and the edges. In addition, we also have additional secondary elements such as lines of symmetry and cross-sections.
In this article, we will take a look at the five Platonic solids and we will learn their main and secondary elements in detail.
Faces of the Platonic solids
The faces of the Platonic solids are the flat surfaces formed at the boundaries of the Platonic solids. Platonic solids have the main characteristic that all their faces are congruent, that is, they have the same shape and size.
Also, the faces of the five platonic solids are regular. Depending on the Platonic solid, we have different numbers of faces and different shapes. For instance,
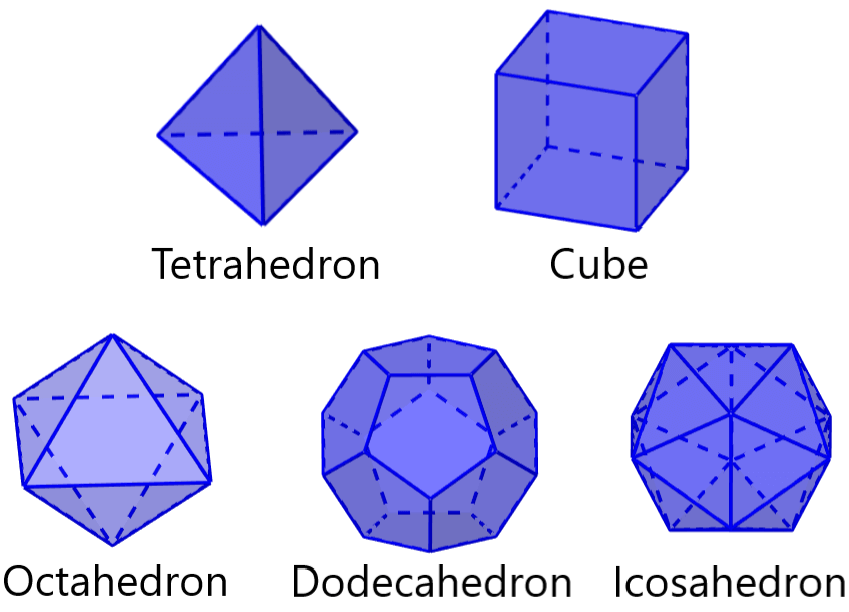
- A tetrahedron has 4 triangular faces.
- A cube has 6 square faces.
- An octahedron has 8 triangular faces.
- A dodecahedron has 12 pentagonal faces.
- An icosahedron has 20 triangular faces.
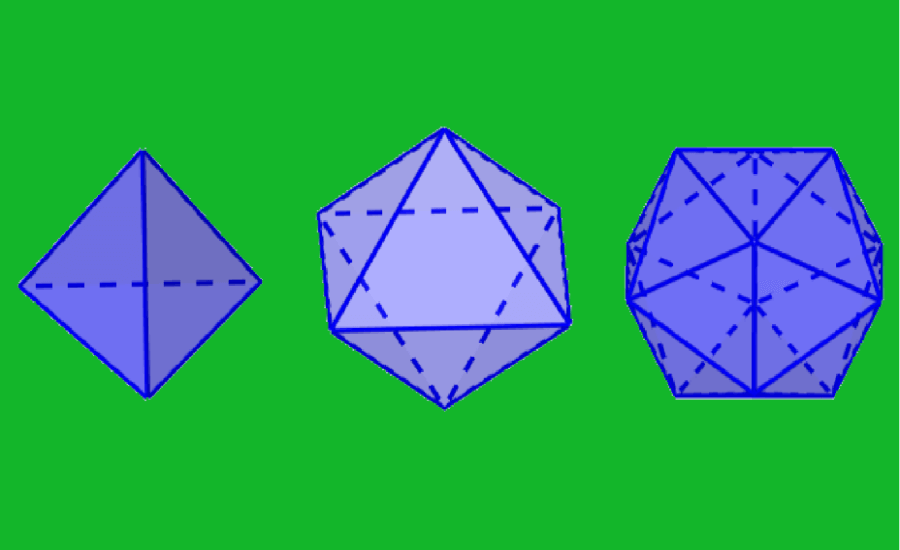
In the case of tetrahedrons, octahedrons, and icosahedrons, the faces are triangular, so each face contains three edges. Also, each face is surrounded by three other faces.
In the case of cubes, each face contains four edges and is surrounded by four other faces. And in the case of dodecahedrons, each face contains five edges and is surrounded by five other faces.
The surface area of the Platonic solids is found by adding the areas of all their faces. That means that if we know the area of one of the faces, we simply have to multiply by the total number of faces.
Vertices of the Platonic solids
The vertices of the Platonic solids are the points where the edges meet. In general, vertices are defined as the points where two or more line segments meet. Therefore, we have:
- A tetrahedron has 4 vertices.
- A cube has 8 vertices.
- An octahedron has 6 vertices.
- A dodecahedron has 20 vertices.
- An icosahedron has 12 vertices.
The number of edges that meet at each vertex depends not only on the shape of the faces but also on the type of Platonic solid. For example, tetrahedrons, octahedrons, and icosahedrons have triangular faces, but a different number of edges intersect at each vertex in all three figures.
- 3 edges of a tetrahedron intersect at each vertex.
- 3 edges of a cube intersect at each vertex.
- 4 edges of an octahedron intersect at each vertex.
- 3 edges of a dodecahedron intersect at each vertex.
- 5 edges of an icosahedron intersect at each vertex.
Edges of the Platonic solids
The edges of the Platonic solids are the line segments that surround each of their faces. In general, we can define edges as the line segments formed by joining two vertices.
Alternatively, we can think of edges as the line segments where two faces of the Platonic solids meet. Each Platonic solid has a different number of edges. Therefore, we have:
- A tetrahedron has 6 edges.
- A cube has 12 edges.
- An octahedron has 12 edges.
- A dodecahedron has 30 edges.
- An icosahedron has 30 edges.
Axis of symmetry
The axis of symmetry is a vertical line that divides the figure into two equal parts. In the case of the Platonic solids, the axis of symmetry is a line through the geometric mean.
If we rotate the Platonic solid with respect to its axis of symmetry, we obtain an equivalent figure from different angles, as shown in the following figure:
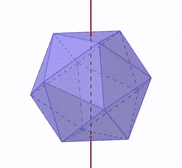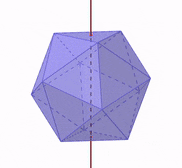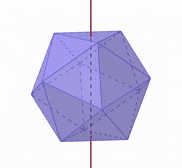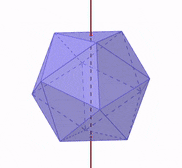
Cross-sections
Cross-sections are the two-dimensional figures formed when a 3D figure is cut by a plane. In the case of the Platonic solids, we can obtain different cross-sections depending on how we cut the figure.
For example, if we cut a cube with a plane that is parallel to the bases, we can obtain a square cross-section as shown in the figure.
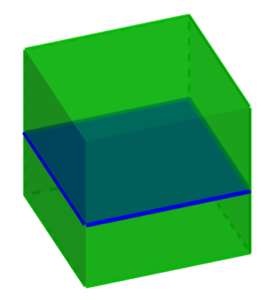
In the case of a tetrahedron, we can form a triangular cross-section if we cut the solid with a plane parallel to its base.
In the case of an octahedron, we will form a square cross-section by cutting the solid with a plane that is perpendicular to its axis of symmetry.
Dodecahedrons and icosahedrons have more complex cross-sections since they are made up of a larger number of faces. Therefore, the cross-section will vary depending not only on the angle but also on the height where we cut the figures.
See also
Interested in learning more about Platonic solids and geometric figures? Look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
