The distance between two points on the coordinate plane can be found by applying the distance formula and substituting the coordinates of the two given points. In turn, the distance formula is derived using the Pythagorean theorem on the Cartesian plane, where the distance represents the hypotenuse of a right triangle.
Here, we will review the distance formula and use it to solve some practice problems.
GEOMETRY
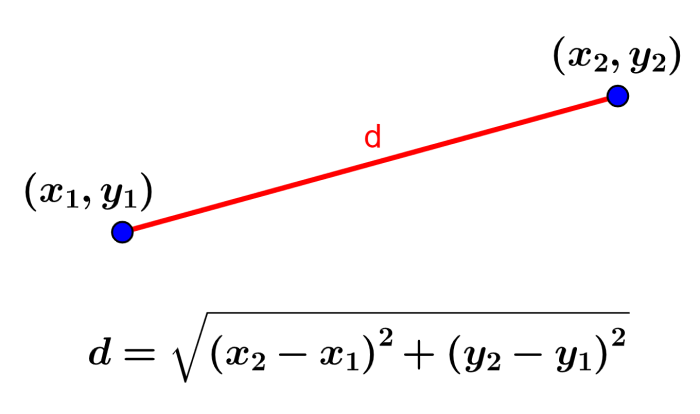
Relevant for…
Learning to calculate the distance between two points with examples.
GEOMETRY
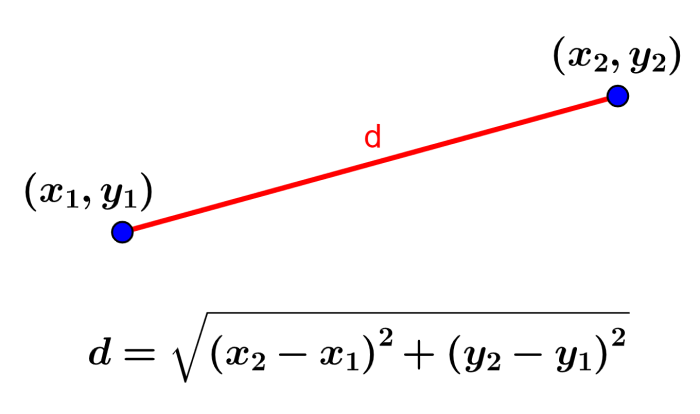
Relevant for…
Learning to calculate the distance between two points with examples.
Review of the formula for the distance between two points
The formula for the distance between two points is obtained when we use the Pythagorean theorem on the Cartesian plane, where the hypotenuse of a right triangle represents the distance between the points.
Also, having the points $latex A = (x_{1}, y_{1})$ and $latex B = (x_{2}, y_{2})$, the vertical distance is equal to $latex |y_{2}-y_{1}|$ and the horizontal distance is equal to $latex |x_{2}-x_{1}|$. Therefore, when we apply the Pythagorean theorem and simplify, we have:
| Formula for the distance $latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$ |
Additionally, we can also expand the distance formula to three-dimensional space as follows:
| Formula for distance in 3D $latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(z_{2}-z_{1})}^2}}$ |
Distance between two points on the coordinate plane – Examples with answers
The distance formulas in 2D and 3D are used to solve the following examples. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
Determine the distance between the points (3, 2) and (6, 6) on the coordinate plane.
Solution
We write the given coordinates as follows:
- $latex (x_{1}, y_{1})=(3, 2)$
- $latex (x_{2}, y_{2})=(6, 6)$
Applying the distance formula with the given coordinates, we have:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(6-3)}^2}+{{(6-2)}^2}}$
$latex =\sqrt{{{(3)}^2}+{{(4)}^2}}$
$latex =\sqrt{9+16}$
$latex =\sqrt{25}$
$latex =5$
The distance between the two points is 5.
EXAMPLE 2
What is the distance between the points (-1, -3) and (5, 7)?
Solution
We have the following values:
- $latex (x_{1}, y_{1})=(-1, -3)$
- $latex (x_{2}, y_{2})=(5, 7)$
In this case, we have negative coordinates. However, the distance formula applies regardless of the signs of the coordinates:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(5-(-1))}^2}+{{(7-(-3))}^2}}$
$latex =\sqrt{{{(6)}^2}+{{(10)}^2}}$
$latex =\sqrt{36+100}$
$latex =\sqrt{136}$
$latex =11.66$
The distance between the points is equal to 11.66.
EXAMPLE 3
If we have the points (-4, -6) and (-1, 5), what is their distance?
Solution
We can write as follows:
- $latex (x_{1}, y_{1})=(-4, -6)$
- $latex (x_{2}, y_{2})=(-1, 5)$
Applying the distance formula, we have:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(-1-(-4))}^2}+{{(5-(-6))}^2}}$
$latex =\sqrt{{{(3)}^2}+{{(11)}^2}}$
$latex =\sqrt{9+121}$
$latex =\sqrt{130}$
$latex =11.4$
The distance between the points is equal to 11.4.
EXAMPLE 4
We have the points (1, 2, 3) and (3, 4, 5) located in three-dimensional space. What is its distance?
Solution
We write the coordinates as follows:
- $latex (x_{1}, y_{1}, z_{1})=(1, 2, 3)$
- $latex (x_{2}, y_{2}, z_{2})=(3, 4, 5)$
In this case, the given points are in three-dimensional space. We can find its distance by using the distance formula in 3D:
$$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(y_{2}-y_{1})}^2}}$$
$latex =\sqrt{{{(3-1)}^2}+{{(4-2)}^2}+{{(5-3)}^2}}$
$latex =\sqrt{{{(2)}^2}+{{(2)}^2}+{{(2)}^2}}$
$latex =\sqrt{4+4+4}$
$latex =\sqrt{12}$
$latex =3.47$
The distance is equal to 3.47.
EXAMPLE 5
If we have the points (-3, 4, -2) and (2, 6, 3), what is their distance?
Solution
We can write as follows:
- $latex (x_{1}, y_{1}, z_{1})=(-3, 4, -2)$
- $latex (x_{2}, y_{2}, z_{2})=(2, 6, 3)$
Similar to the previous exercise, we have to use the distance formula in 3D with the given coordinates. Therefore, we have:
$$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(y_{2}-y_{1})}^2}}$$
$$=\sqrt{{{(2-(-3))}^2}+{{(6-4)}^2}+{{(3-(-2))}^2}}$$
$latex =\sqrt{{{(5)}^2}+{{(2)}^2}+{{(5)}^2}}$
$latex =\sqrt{25+2+25}$
$latex =\sqrt{52}$
$latex =7.21$
The distance is equal to 7.21.
Distance between two points – Practice problems
Use the distance formulas in both 2D and 3D to solve the following problems. In case you need help with this, you can look at the solved examples above.
See also
Interested in learning more about distance, midpoint, and slope on the plane? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
