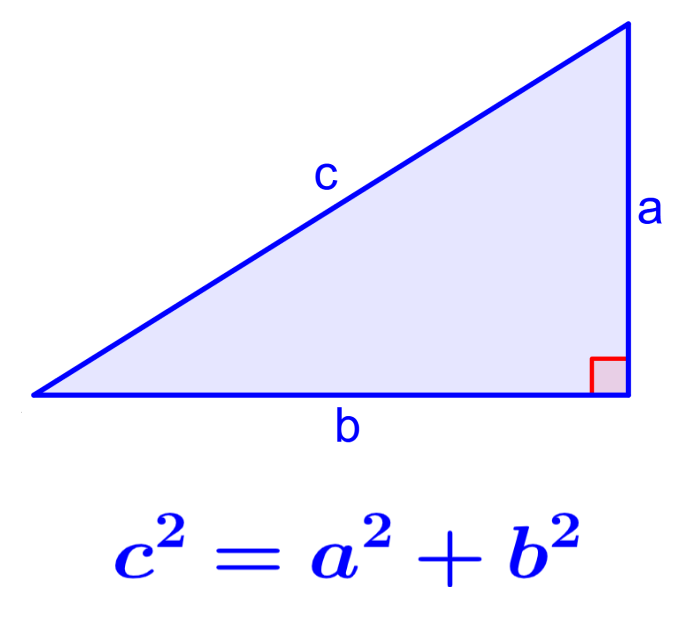
The Pythagorean theorem is an equation or formula that allows us to relate the three sides of a right triangle. In geometry, the Pythagorean theorem is mainly used to determine the lengths of the sides of a right triangle. Additionally, this theorem is used to derive other important formulas such as Pythagorean identities.
Here, we will briefly review the Pythagorean theorem. We will look at its formula and we will apply it to solve some exercises.
Pythagorean theorem formula
The Pythagorean theorem is a way of relating the lengths of the three sides in a right triangle. The Pythagorean theorem says that the square of the hypotenuse is equal to the sum of the squares of the legs.
Recall that the hypotenuse is the side of the triangle opposite the right angle (90°) and the legs are the other two sides of the triangle. We are going to use the following triangle to illustrate this:
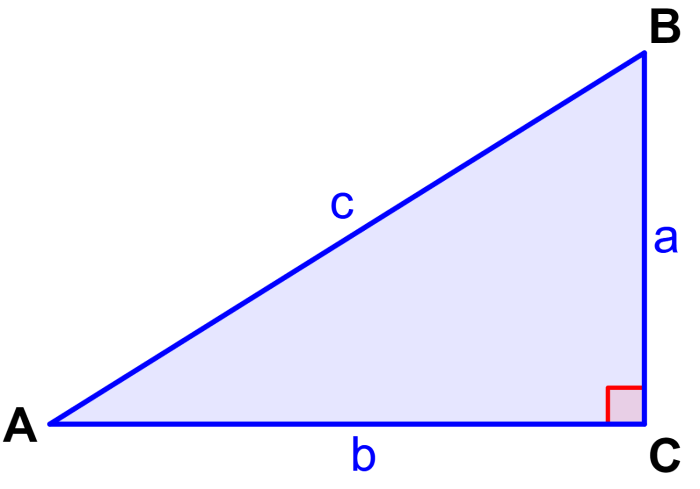
In this triangle, the formula of the Pythagorean theorem is:
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
where a and b are the lengths of the legs of the triangle and c is the length of the hypotenuse.
We can use the Pythagorean theorem when we want to solve any of the following situations:
- We know the lengths of the two legs and we want to find the length of the hypotenuse.
- We know the length of the hypotenuse and the length of one leg and we want to find the length of the other leg.
Exercises with answers of Pythagorean theorem
The following exercises show how to apply the Pythagorean Theorem to solve problems. Try to solve the exercises yourself before looking at the solution.
EXERCISE 1
Find the length of X in the triangle below.
Solution
The length of X corresponds to the hypotenuse of the triangle. In addition, we have the following lengths:
- a=6
- b=8
We use the Pythagorean theorem with these values and we have:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{6}^2}+{{8}^2}$
$latex {{c}^2}=36+64$
$latex {{c}^2}=100$
$latex c=\sqrt{100}$
$latex c=10$
The length X is 10.
EXERCISE 2
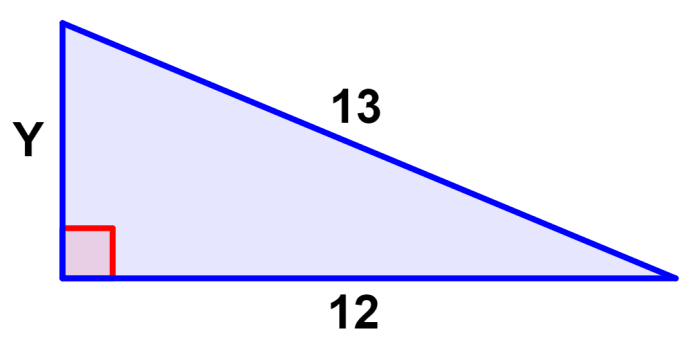
What is the length of Y in the triangle below?
Solution
In this case, we have to find the length of one of the legs and we have the following lengths:
- a=12
- c=13
We use these lengths in the Pythagorean theorem and we have:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{13}^2}={{12}^2}+{{b}^2}$
$latex 169=144+{{b}^2}$
$latex {{b}^2}=169-144$
$latex {{b}^2}=25$
$latex b=5$
The length of b is 5.
EXERCISE 3
What is the hypotenuse of a right triangle that has legs of length 12 and 16?
Solution
We have the lengths of the legs:
- a=12
- b=16
We apply the Pythagorean theorem with these lengths to find the length of the hypotenuse:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{12}^2}+{{16}^2}$
$latex {{c}^2}=144+256$
$latex {{c}^2}=400$
$latex c=20$
The hypotenuse measures 20.
EXERCISE 4
A right triangle has a hypotenuse of 11 and a leg of 7? Determine the length of the other leg.
Solution
We have the following lengths:
- a=7
- c=11
We find the length of the other leg using the Pythagorean theorem:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{11}^2}={{7}^2}+{{b}^2}$
$latex 121=49+{{b}^2}$
$latex {{b}^2}=121-49$
$latex {{b}^2}=72$
$latex b=8.5$
The length of the other leg is 8.5.
EXERCISE 5
Two cyclists go out for a ride at the same time, one going south and the other going west. After half an hour, the cyclist who went south has traveled 7 kilometers and the cyclist who went west has traveled 8.5 kilometers. At that time, what is the shortest distance between the two?
Solution
We are going to use a diagram to facilitate the resolution of this problem.
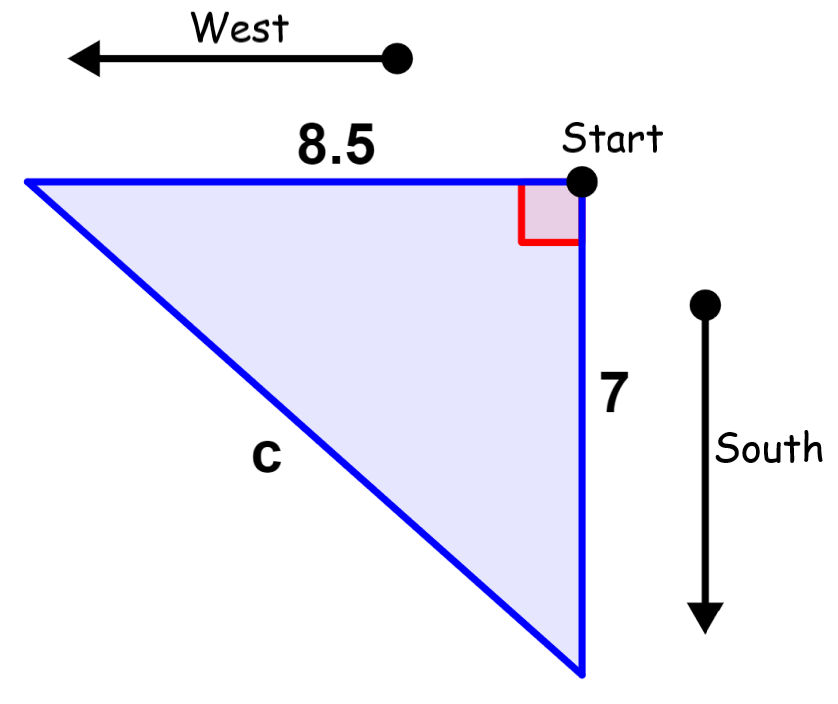
The south and west directions form a right angle, and the shortest distance between two points is a straight line. This means that the distance we want to find is equal to the hypotenuse of the triangle formed. Therefore, we use the Pythagorean theorem:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{7}^2}+{{8.5}^2}$
$latex {{c}^2}=49+72.25$
$latex {{c}^2}=121.25$
$latex c=11.01$
The shortest distance between the two is 11.01 kilometers.
Pythagorean theorem – Exercises to solve
Solve the following practice exercises applying the Pythagorean theorem. Select your obtained answer and check it to verify that you got the correct answer.
See also
Interested in learning more about the Pythagorean theorem? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
