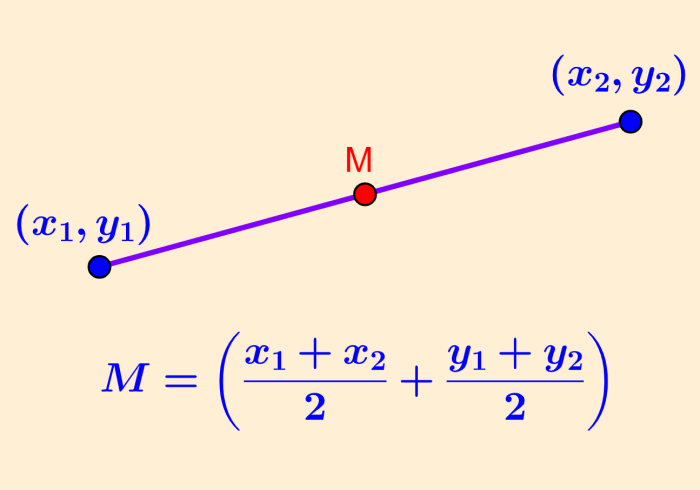
The midpoint of a line segment is a point that has coordinates that are located exactly in the middle of the two endpoints of the line segment. These coordinates can be found by adding the x-coordinates of the two points and dividing by 2. Similarly, we add the y-coordinates of the two points and divide by 2.
Here, we will look at the formula that we can use to determine the coordinates of the midpoint. Then, we will use that formula to solve some practice problems.
How to determine the coordinates of the midpoint of a line segment?
To determine the coordinates of the midpoint of a line segment, we have to use the midpoint formula. This formula is derived considering that the x-coordinates of the midpoint will be equal to the sum of the x-coordinates of the points divided by 2 and the y-coordinates of the midpoint will be equal to the sum of the y-coordinates of the points divided by 2.
Therefore, if we have points A and B with the coordinates $latex A = (x_{1}, y_{1})$ and $latex B = (x_{2}, y_{2} )$, the midpoint formula is:
| Formula for the midpoint $latex M=\left( \frac{x_{1}+x_{2}}{2}+\frac{y_{1}+y_{2}}{2}\right)$ |
The midpoint will be expressed as the coordinates $latex M = (x_{3}, y_{3})$.
Examples with answers of midpoint of a line segment
The midpoint formula is used to determine the coordinates of the midpoint between the given points. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
Determine the coordinates of the midpoint between the points (1, 4) and (5, 8).
Solution
We have the following two points:
- $latex (x_{1}, y_{1})=(1, 4)$
- $latex (x_{2}, y_{2})=(5, 8)$
Applying the midpoint formula with the given points, we have:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{1+5}{2},\frac{4+8}{2}\right)$
$latex =\left(\frac{6}{2},\frac{12}{2}\right)$
$latex =(3,6)$
The coordinates of the midpoint are $ latex M = (3,6) $.
EXAMPLE 2
What are the coordinates of the midpoint between the points (3, 5) and (11, 13)?
Solution
We have the following coordinates:
- $latex (x_{1}, y_{1})=(3, 5)$
- $latex (x_{2}, y_{2})=(11, 13)$
We use these coordinates in the midpoint formula and we have:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{3+11}{2},\frac{5+13}{2}\right)$
$latex =\left(\frac{14}{2},\frac{18}{2}\right)$
$latex =\left(7,9\right)$
The coordinates of the midpoint are $latex M=(7, 9)$.
EXAMPLE 3
If we have the points (-3, -5) and (5, 8), what is their midpoint?
Solution
We can write as follows:
- $latex (x_{1}, y_{1})=(-3, -5)$
- $latex (x_{2}, y_{2})=(5, 8)$
This exercise has a point with negative coordinates, however, similar to the previous exercises, we simply apply the midpoint formula:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{-3+5}{2},\frac{-5+8}{2}\right)$
$latex =\left(\frac{2}{2},\frac{3}{2}\right)$
$latex =\left(1,\frac{3}{2}\right)$
The midpoint has the coordinates $latex M=\left(1,\frac{3}{2}\right)$.
EXAMPLE 4
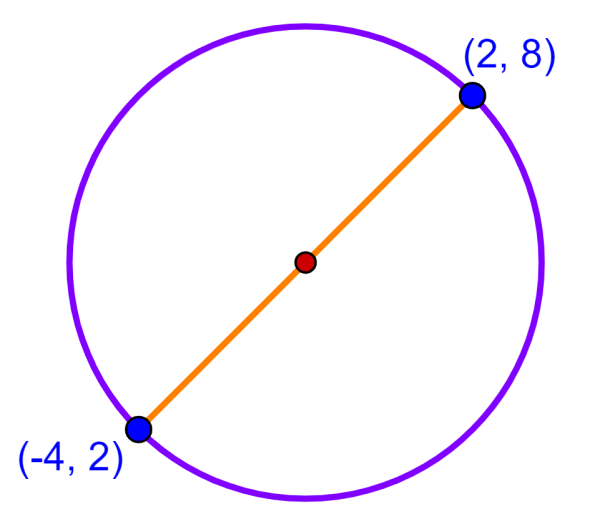
A circle has a diameter that is bounded by the points (-4, 2) and (2, 8). Determine the coordinates of the center of the circle.
Solution
Remember that the center is exactly half the diameter of the circle. Therefore, we can find the coordinates of the center by finding the coordinates of the midpoint of the following two points:
- $latex (x_{1}, y_{1})=(-4,2)$
- $latex (x_{2}, y_{2})=(2,8)$
Using the midpoint formula with these coordinates, we have:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{-4+2}{2},\frac{2+8}{2}\right)$
$latex =\left(\frac{-2}{2},\frac{12}{2}\right)$
$latex =(-1,7)$
The coordinates of the center of the circle are $latex (-1, 7)$.
EXAMPLE 5
We have the two points (m, 2) and (9, 12). Determine the value of m if the midpoint is (2, 7).
Solution
We have the following coordinates:
- $latex (x_{1}, y_{1})=(m, 2)$
- $latex (x_{2}, y_{2})=(9, 12)$
- $latex (x_{3}, y_{3})=(2, 7)$
Using the midpoint formula with the given coordinates, we have:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{m+9}{2},\frac{2+12}{2}\right)$
The value of m is part of the x coordinates of the midpoint, so we only have to consider the x component. Therefore, we form an equation and solve for p. We use the x coordinate of the midpoint which is 2:
$latex 2=\left(\frac{m+9}{2}\right)$
$latex 4=m+9$
$latex m=-5$
The value of m is -5.
Midpoint of a line segment – Practice problems
Apply what you have learned about the midpoint to solve the following problems. In case you need help with this, you can look at the solved examples above.
See also
Interested in learning more about the midpoint, slope, and distance on the plane? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
