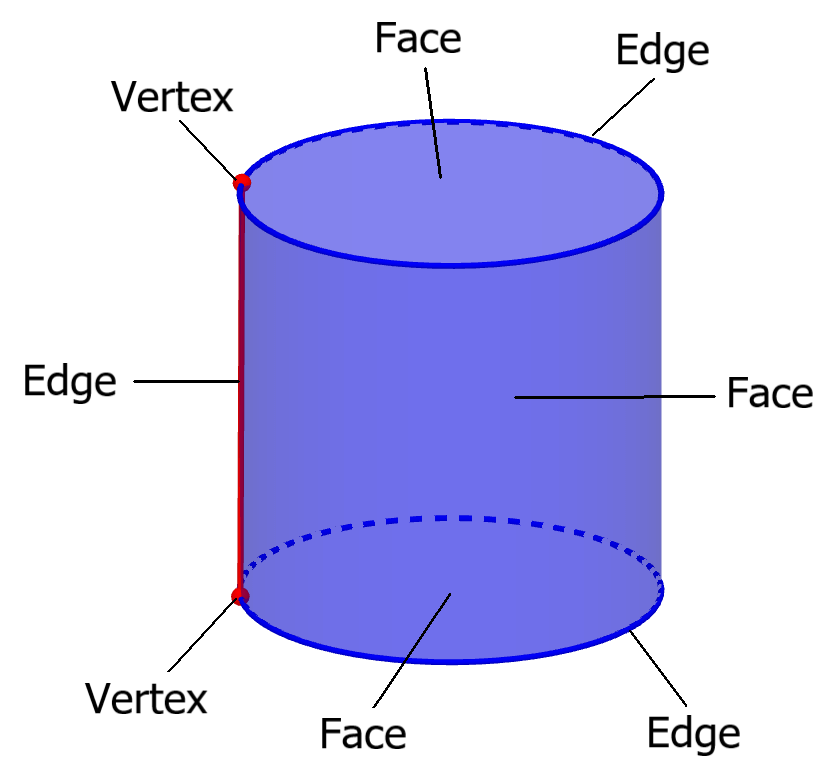
The cylinder is not a polyhedron, so the faces, the vertices and the edges of the cylinders are considered in a slightly different way than polyhedra like the cube, the prism and others. However, we can give it a structure similar to the structure of polyhedra, specifically we give it a CW complex structure. In summary, a CW complex is similar to a polyhedron, with the exception that the faces and edges can have curvature. Using this, we can determine that a cylinder has 3 faces, 3 edges, and 2 vertices.
Here, we will learn more about the faces, vertices, and edges of cubes using diagrams.
Faces found in a cylinder
Unlike the faces of polyhedra, not all cylinder faces are planar surfaces. Cylinders are made up of three faces, two circular faces that form the bases of the cylinder and one face formed by the rest of the surface of the cylinder. If we extended the cylinder, the third face would have the shape of a rectangle as shown in the diagram:
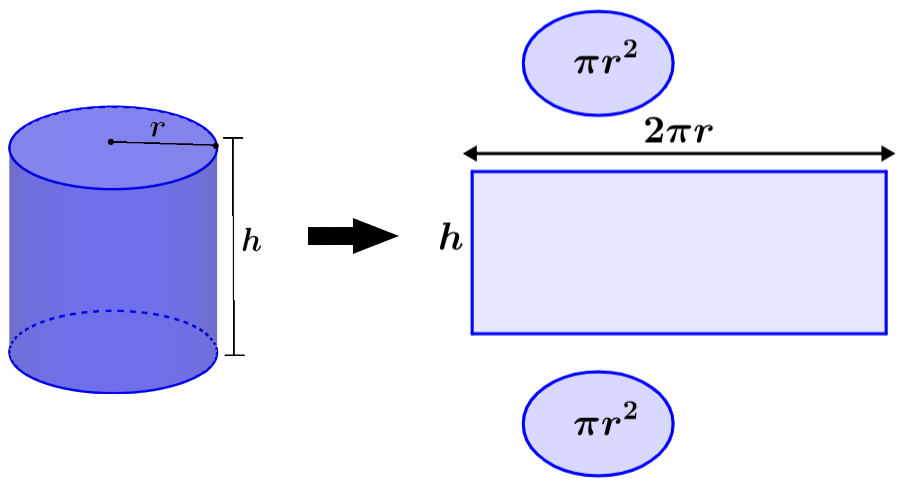
If we add the areas of the three faces, we will obtain the surface area of the cylinder. We know that each circular face must have an area of πr², so the two bases have an area of 2πr². The third face is formed by stretching the surface that joins the bases.
By stretching this surface, we form a rectangle that has a length equal to the circumference of the circular bases and a height equal to the height of the cylinder. Therefore, the area of this surface is 2πrh. The total surface area is equal to 2πr² + 2πrh.
Vertices found in a cylinder
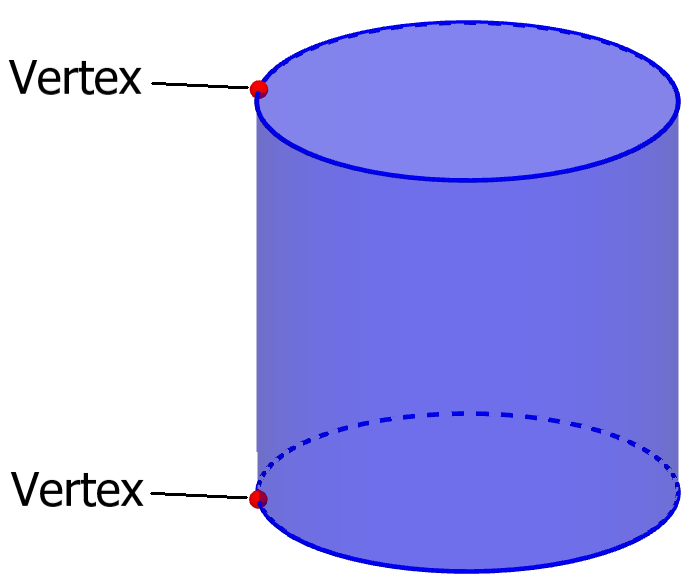
In the case of polyhedra, vertices are the points where two line segments meet. For cylinders, we are considering the CW complex structure, as mentioned in the introduction. This allows us to take into account faces that have curved surfaces and edges that also have curvature.
Therefore, we can conclude that we have two vertices in a cylinder, one in each circle. We can interpret this as the point we mark when we begin to trace a circle and where we finish a complete turn.
In addition, we can also consider those points, as the places where the curved surface of the cylinder is joined.
Edges found in a cylinder
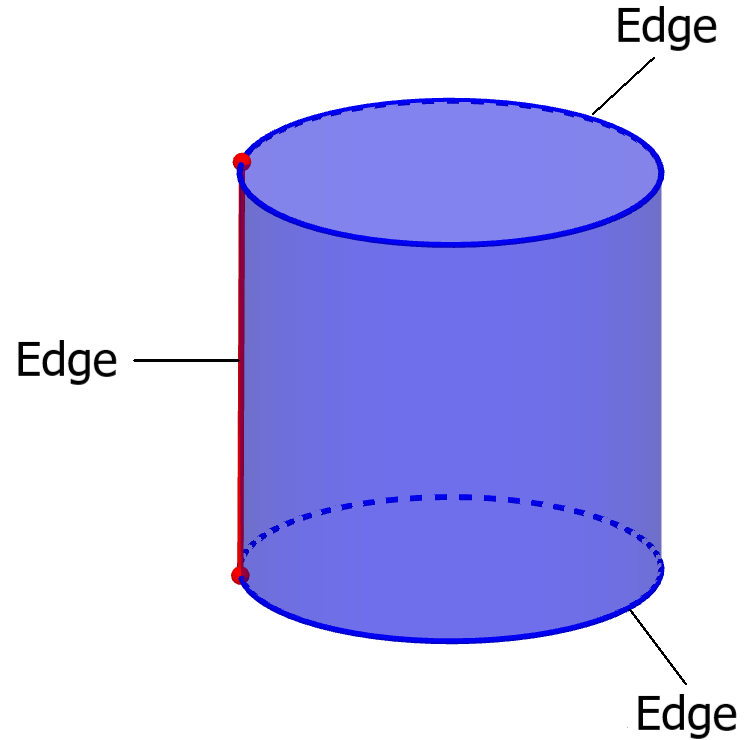
The edges are considered as line segments at the limits of polyhedra that join two vertices. However, in cylinders, we have two edges that have curvature, which are the circumferences of the circles at the bases.
In addition, we have a third edge that joins the two vertices of the circles and that is located along the lateral face. Therefore, we have a total of 3 edges.
We have seen that a cylinder has 3 faces, 2 vertices, and 3 edges. This complies with the Euler characteristic, which is a definite number that allows us to describe the shape or structure of polyhedra or topological spaces.
Therefore, the Euler characteristic of a cylinder is 2-3 + 3 = 2, which agrees with the Euler characteristic of 2 of a sphere. This is correct since a cylinder is homotopically equivalent to a sphere.
See also
Interested in learning more about cylinders? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
