Thales’ theorem tells us that a triangle inscribed in a circle, where the hypotenuse corresponds to the diameter of the circle, is always a right triangle. This theorem can be proved using the sum of interior angles.
Here, we will look at a summary of Thales’ theorem. Then, we will learn to apply this theorem to solve some practice problems.
Summary of Thales’ theorem
Thales’ theorem is considered as a special case of the inscribed angles theorem. This theorem tells us that, if we have a triangle inscribed in a circle as shown in the following diagram, the angle formed at vertex B is always a right angle.
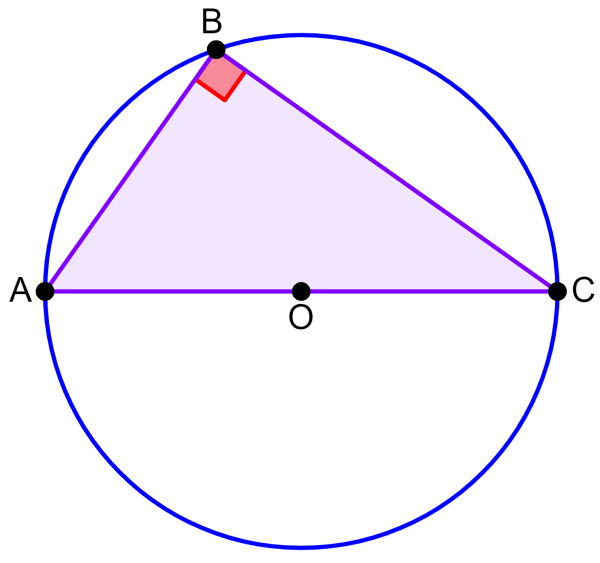
Therefore, if three points A, B, and C are located on the circumference of a circle, where line AC is the diameter of the circle, then the angle ∠ABC is a right angle (90°).
This theorem can be proved by drawing a bisector from the center to vertex B and then using the angles of the isosceles triangles formed and the fact that the sum of interior angles of any triangle is equal to 180°. You can look at the full proof in this article.
Thales’ theorem – Examples with answers
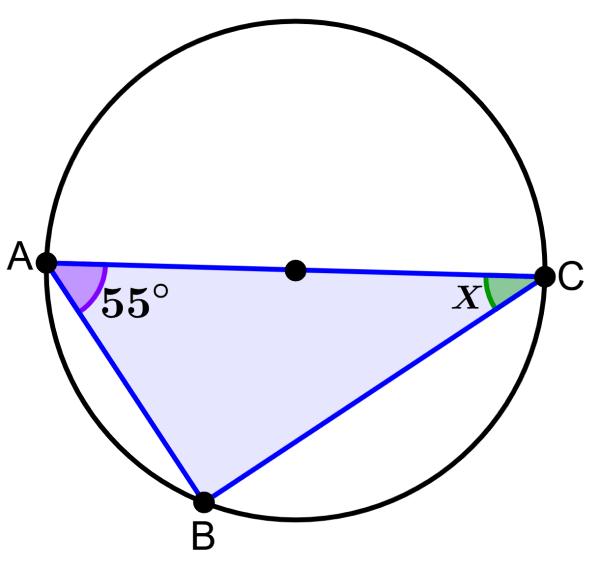
EXAMPLE 1
Segment AC is the diameter of the circle. What is the measure of angle Z?
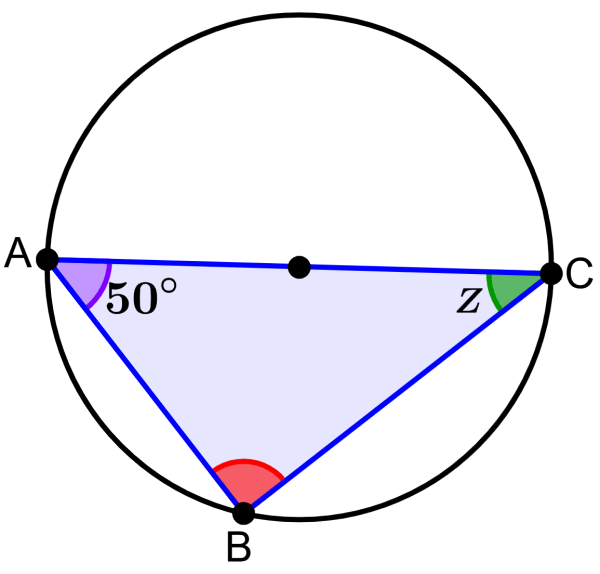
Solution
The segment AC is the diameter of the circle, so we can use Thales’ theorem. Therefore, we know that the angle at vertex B is a 90° angle. Since the sum of interior angles in any triangle is equal to 180°, we have:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
The measure of angle Z is 40°.
EXAMPLE 2
Determine the measure of angle Z in the diagram below if segment AC is the diameter of the circle.
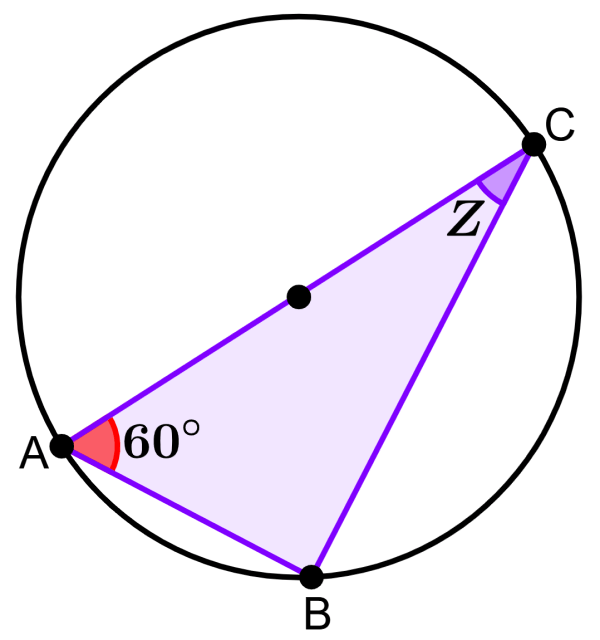
Solution
The segment AC is the diameter of the circle, so we can use Thales’ theorem. Therefore, we know that the angle at vertex B is a 90° angle. Since the sum of interior angles in any triangle is equal to 180°, we have:
90°+60°+Z=180°
150°+Z=180°
Z=180°-150°
Z=30°
The measure of angle Z is 30°.
EXAMPLE 3
If M is the center of the circle, determine the measure of angle Z.
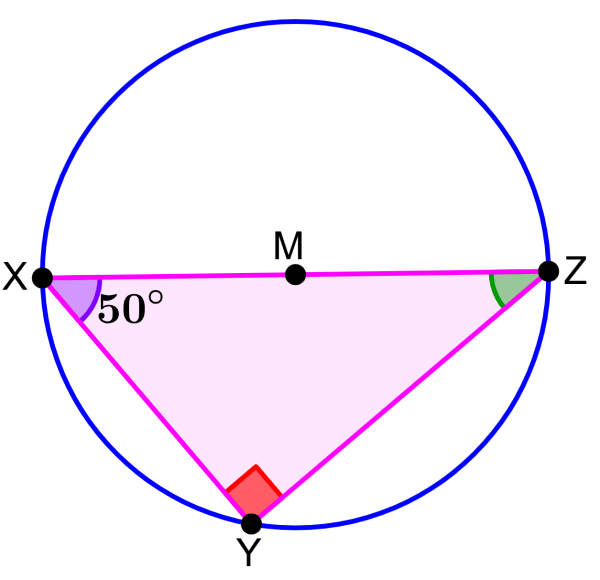
Solution
Since point M is the center of the circle, we know that segment XZ is the diameter of the circle. Therefore, we can use Thales’ theorem.
By the theorem, we know that the angle at vertex Y is a right angle, that is, a 90° angle. We can use the sum of interior angles of a triangle to get the measure of Z:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
The measure of angle Z is 40°.
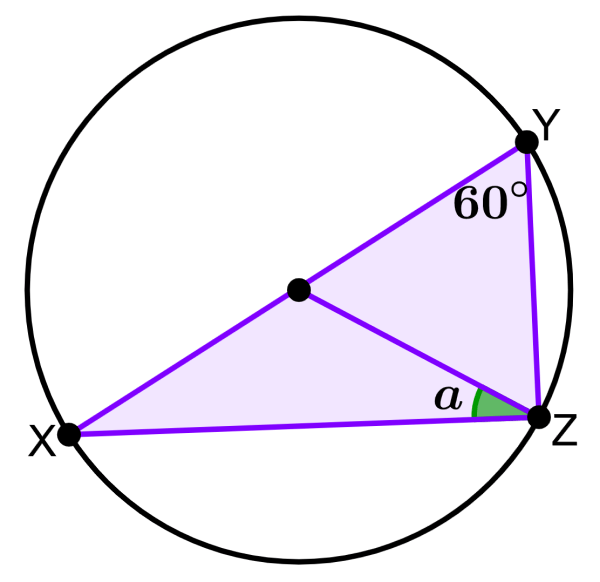
EXAMPLE 4
If O represents the center of the circle, what is the measure of angle a?
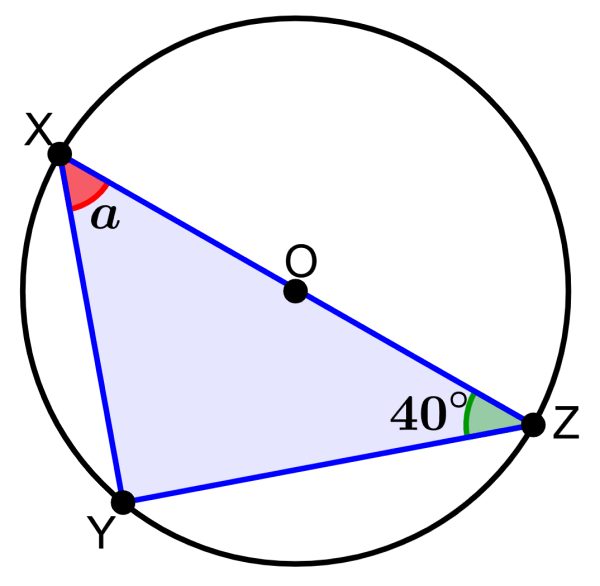
Solution
If point O is the center of the circle, we know that segment XZ represents the diameter of the circle. Therefore, we can apply Thales’ theorem. Using the theorem, we know that angle Y is right, that is, 90°.
Now, we use the sum of interior angles of a triangle to find the measure of angle a:
90°+40°+a=180°
130°+a=180°
a=180°-130°
a=50°
The measure of angle a is 50°.
EXAMPLE 5
Segment AC is the diameter of the circle. What is the length of the diameter?
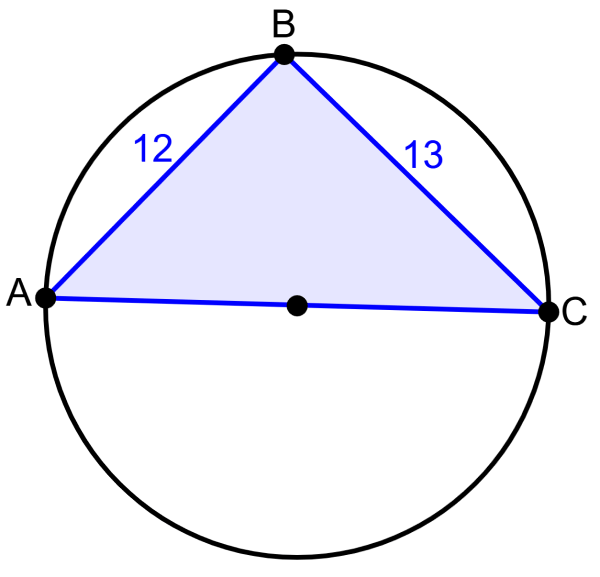
Solution
Using Thales’ theorem, we can determine that triangle ABC is a right triangle. This means that angle B is a right angle. Therefore, we can use the Pythagorean theorem to find the length of the diameter:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{12}^2}+{{13}^2}$
$latex {{c}^2}=144+169$
$latex {{c}^2}=313$
$latex c=17.7$
The length of segment AC is 17.7 units.
EXAMPLE 6
If segment XY is the diameter of the circle, what is its length?
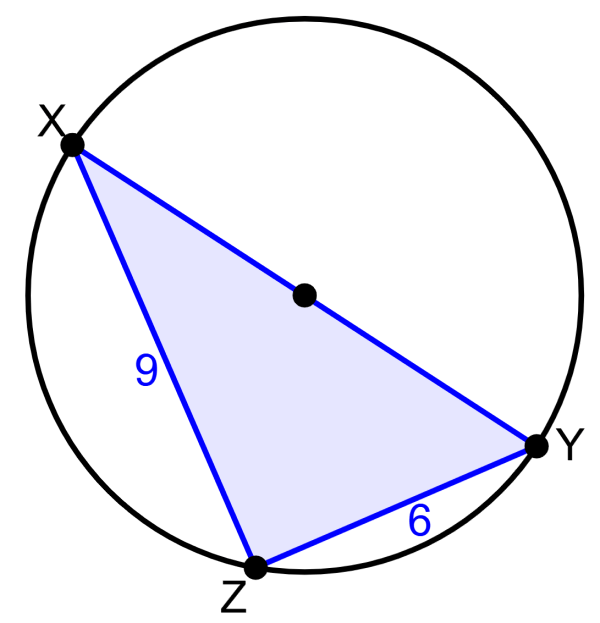
Solution
Applying Thales’ theorem, we find that triangle XYZ is a right triangle. That is, angle Z is a right angle. Therefore, we find the length of XY by applying the Pythagorean theorem, where, XY is the hypotenuse of a right triangle:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{6}^2}+{{9}^2}$
$latex {{c}^2}=36+81$
$latex {{c}^2}=117$
$latex c=10.82$
The length of the XY segment is 10.82 units.
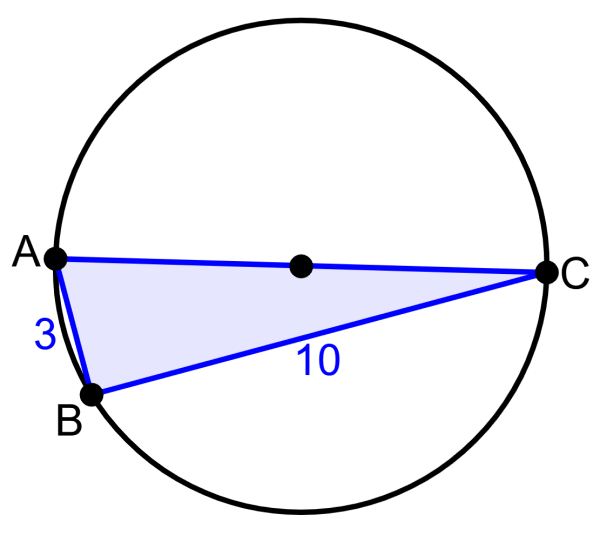
EXAMPLE 7
Determine the length of segment AB in the diagram below.
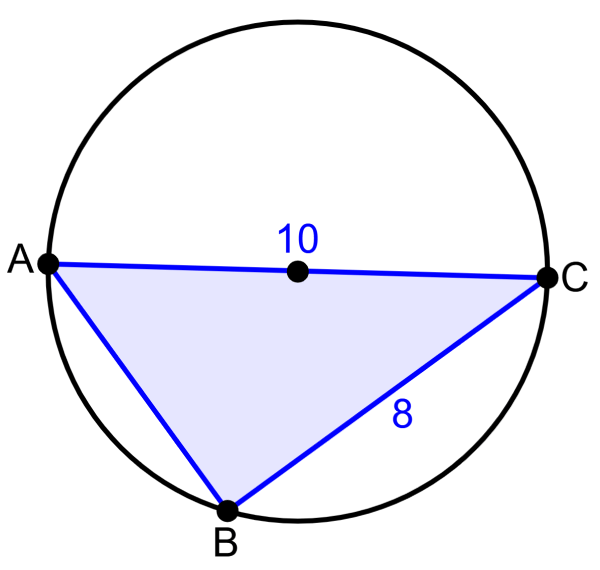
Solution
Segment AC is the diameter of the circle. Then, applying Thales’ theorem, we can determine that triangle ABC is a right triangle. Therefore, we use the Pythagorean theorem to find the length of segment AB:
$latex {{a}^2}+{{b}^2}={{c}^2}$
$latex {{a}^2}+{{8}^2}={{10}^2}$
$latex {{a}^2}+64=100$
$latex {{a}^2}=100-64$
$latex {{a}^2}=36$
$latex a=6$
The length of segment AB is 6 units.
EXAMPLE 8
What is the length of AC if AB is the diameter of the circle?
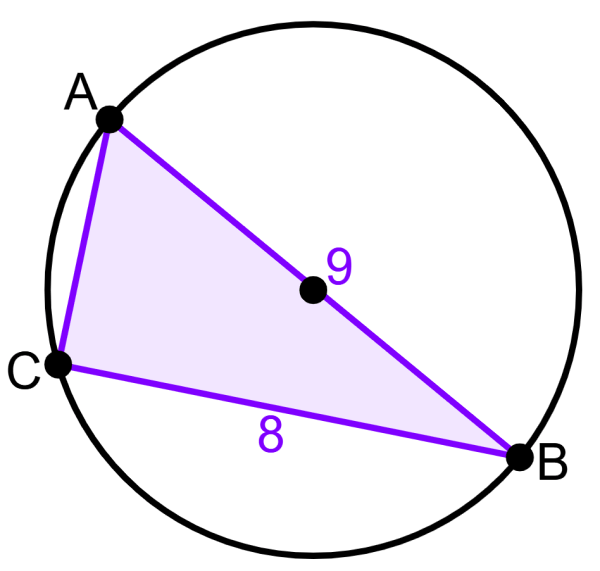
Solution
Since AB is the diameter of the circle, we know that Thales’ theorem applies. This means that the triangle is a right triangle and we can use the Pythagorean theorem to find the length of the segment AC:
$latex {{a}^2}+{{b}^2}={{c}^2}$
$latex {{a}^2}+{{8}^2}={{9}^2}$
$latex {{a}^2}+64=81$
$latex {{a}^2}=81-64$
$latex {{a}^2}=17$
$latex a=4.12$
The length of segment AC is 4.12 units.
EXAMPLE 9
If C is the center of the circle, what is the measure of angle ∠ABC?
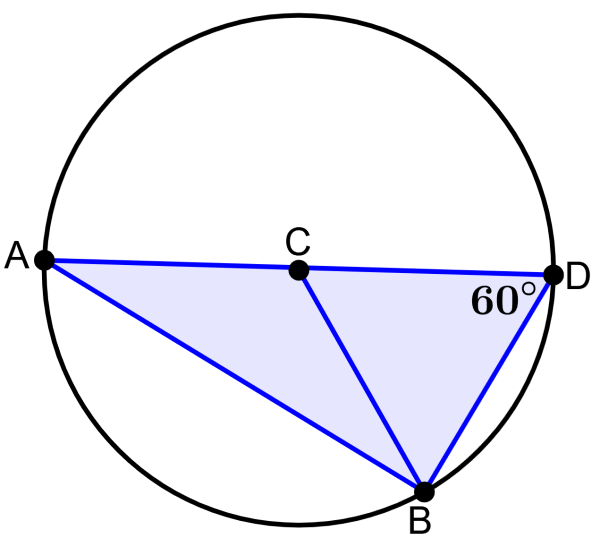
Solution
Since point C is the center of the circle, we know that segment AD is the diameter. Therefore, we can apply Thales’ theorem.
Two of the sides of the triangles ABC and BCD are equal since they correspond to the radii of the circle. Therefore, two angles are also equal and the triangles must be isosceles triangles. So, we have:
∠CBD = ∠CDB = 60°
Applying Thales’ theorem, we have:
∠ABD = 90°
So, we have:
∠ABC = 90°-60° = 30°
Therefore, the measure of angle ∠ABC is 30°.
Thales’ theorem – Practice problems
See also
Interested in learning more about Thale’s theorem? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
