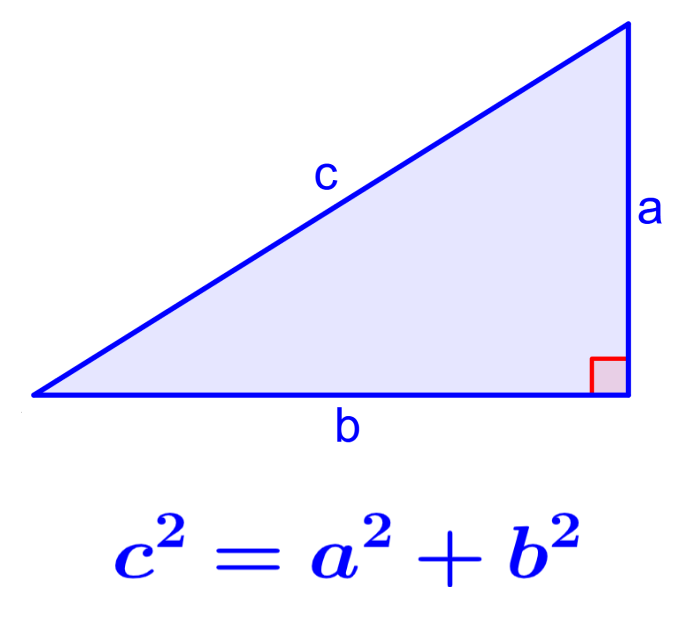
The Pythagorean theorem is one of the most commonly known formulas in mathematics. This theorem defines the relationship between the sides of a right triangle. The Pythagorean theorem is used to find the lengths of some unknown side in a right triangle. Furthermore, through the Pythagorean theorem, other important mathematical formulas are derived, such as Pythagorean identities.
Here, we will look at a summary of the Pythagorean theorem along with some practice examples.
Summary of the Pythagorean theorem
The Pythagorean theorem is a formula that relates the sides of a right triangle. The Pythagorean theorem states that “In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.” We can illustrate this idea using the following triangle:
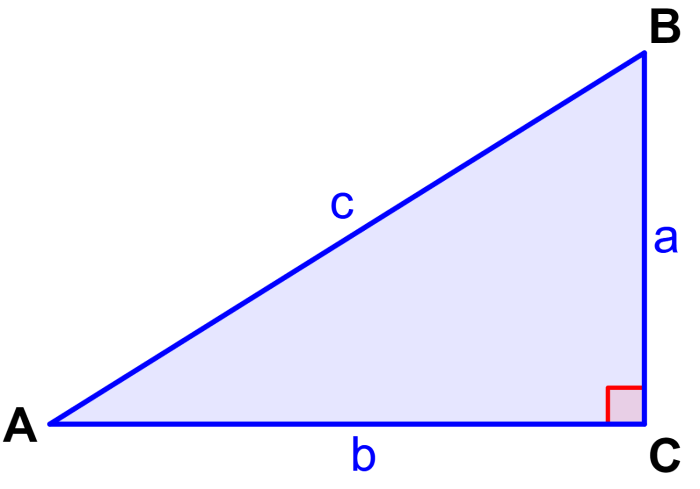
In this triangle, the Pythagorean theorem is equal to
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
where, a, b represent the legs of the triangle and c represents the hypotenuse.
The Pythagorean theorem can be applied in the following situations:
- We want to find the length of the hypotenuse and we have the lengths of the two legs.
- We want to find the length of one leg and we know the length of the hypotenuse and the length of the other leg.
Pythagorean theorem – Examples with answers
The following examples show how to apply the Pythagorean Theorem to solve problems. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Determine the length of X using the Pythagorean theorem.
Solution
The length we want to find corresponds to the hypotenuse of the triangle. Therefore, we have the two lengths of the legs:
- a=3
- b=4
We apply the Pythagorean theorem using the two given lengths and we have:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{3}^2}+{{4}^2}$
$latex {{c}^2}=9+16$
$latex {{c}^2}=25$
$latex c=\sqrt{25}$
$latex c=5$
The length of X is 5.
EXAMPLE 2
Use the Pythagorean theorem to find the missing length.
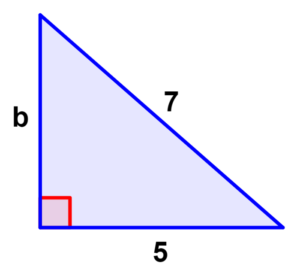
Solution
We have the length of the hypotenuse and one of the legs and we want to find the length of the other leg. Therefore, we extract the following:
- a=5
- c=7
Using the Pythagorean theorem with these values, we have:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{7}^2}={{5}^2}+{{b}^2}$
$latex 49=25+{{b}^2}$
$latex {{b}^2}=49-25$
$latex {{b}^2}=24$
$latex b=4.9$
The length of b is 4.9.
EXAMPLE 3
A right triangle has legs of lengths 9 and 13. What is the length of its hypotenuse?
Solution
From the question, we have the following lengths:
- a=9
- b=13
Therefore, we are going to use these values in the Pythagorean theorem to find the length of the hypotenuse:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{9}^2}+{{13}^2}$
$latex {{c}^2}=81+169$
$latex {{c}^2}=250$
$latex c=15.8$
The hypotenuse measures 15.8.
EXAMPLE 4
What is the length of the other leg of a right triangle that has a hypotenuse of 18 and a leg of 12?
Solution
We have the following values:
- a=12
- c=18
Therefore, we use the Pythagorean theorem together with these values to find the value of b:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{18}^2}={{12}^2}+{{b}^2}$
$latex 324=144+{{b}^2}$
$latex {{b}^2}=324-144$
$latex {{b}^2}=180$
$latex b=13.4$
The length of the other leg is 13.4.
EXAMPLE 5
Carlos wants to clean the window of his building, which is located 4 m high. He has a ladder that is 4.5 m. How far from the building should he place the ladder?
Solution
The length of the ladder is fixed and when placing it inclined in the building, we form a right triangle, where the ladder is the hypotenuse, the building is the height and the base is the distance from the building to the ladder. Therefore, we have the following values:
- a=4
- c=4.5
We have to use the Pythagorean theorem to find the value of b:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{4.5}^2}={{4}^2}+{{b}^2}$
$latex 20.25=16+{{b}^2}$
$latex {{b}^2}=20.25-16$
$latex {{b}^2}=4.25$
$latex b=2.06$
The distance from the building to where the ladder should be placed is 2.06 m.
Pythagorean theorem – Practice problems
Apply the Pythagorean theorem to solve the following problems. Select an answer and check it to see if you got the correct answer.
See also
Interested in learning more about the Pythagorean theorem? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
