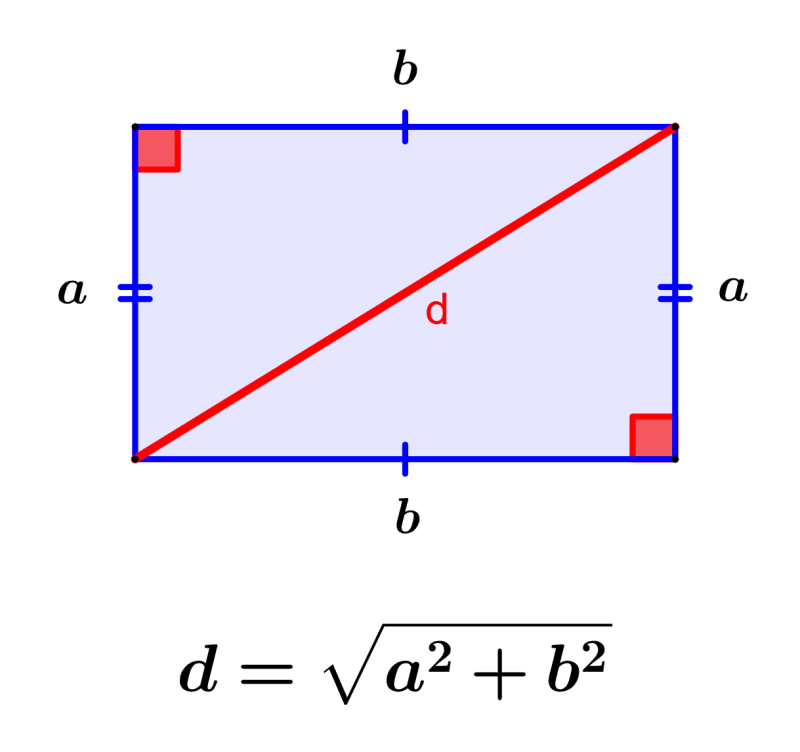
The diagonal is the line that runs from one corner of the rectangle to the opposite corner and passes through the center of the rectangle. Diagonals are lines that join two non-adjacent vertices of a polygon, that is, diagonals join two vertices of the figure excluding the sides of the polygon. Diagonals are calculated using the diagonal formula.
Here, we will learn about the formula for the diagonal of a rectangle and we will look at several examples that use this formula.
How to find the diagonal of a rectangle?
We can find the length of the diagonal of a rectangle using the following formula:
$latex d = \sqrt{{{a}^2}+{{b}^2}}$
where,
- a is the length of the height of the rectangle
- b is the length of the base of the rectangle
- d is the length of the diagonal
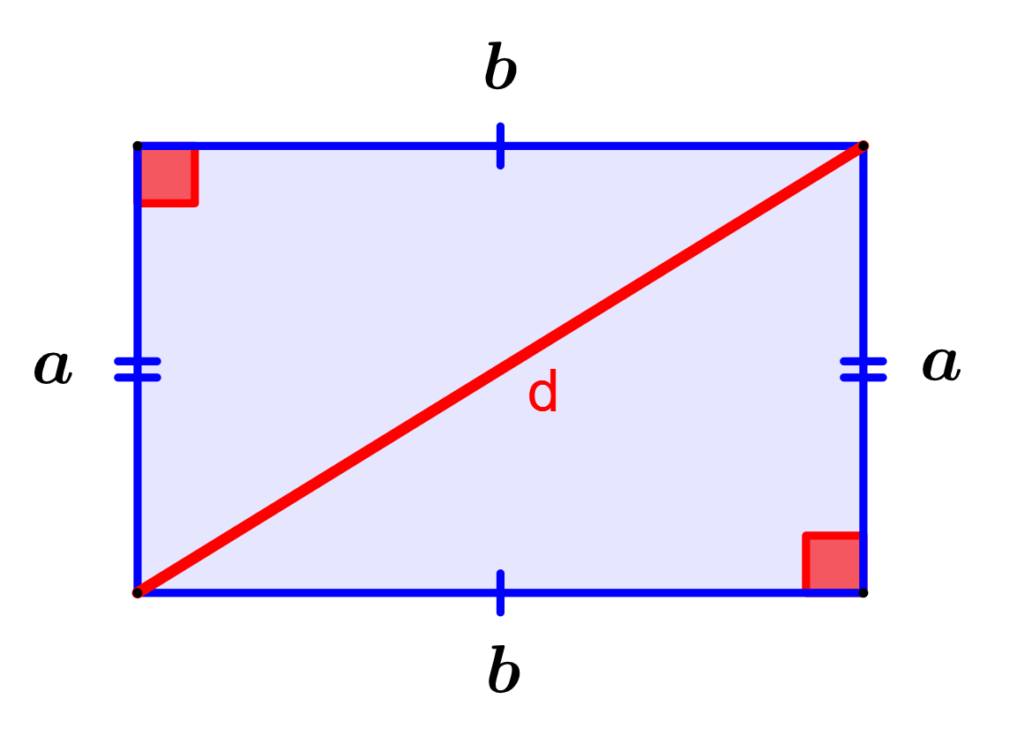
This formula is derived from the Pythagorean theorem. We can see that a diagonal of the rectangle divides it into two equal right triangles. The diagonal of the rectangle is the hypotenuse of these triangles.
Using the Pythagorean theorem, we can find the length of the diagonal (the hypotenuse) if we know the lengths of the base and the height of the rectangle.
Diagonals of rectangles have the following properties:
• The two diagonals are congruent (they have the same length).
• Each diagonal bisects the other. This means that the point where the diagonals intersect divides each diagonal into two equal parts.
• Each diagonal divides the rectangle into two congruent right triangles. This means that each triangle has half the area of the rectangle.
Diagonal of a rectangle – Examples with answers
The following examples are solved using the diagonal formula indicated above. Each example has its respective solution, but you should try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
What is the length of the diagonal of a rectangle with sides that have a length of 3 m and 4 m?
Solution
We have the information:
- Base = 3 m
- Height = 4 m
The formula for the diagonal of a rectangle is $latex d= \sqrt{{{a}^2}+{{b}^2}}$. Therefore, using the given information, we have:
$latex d=\sqrt{{{a}^2}+{{b}^2}}$
$latex d=\sqrt{{{3}^2}+{{4}^2}}$
$latex d=\sqrt{9+16}$
$latex d=\sqrt{25}$
$latex d=5$
The diagonal of the rectangle is 5 m.
EXAMPLE 2
A rectangle has a base that is 12 cm and a height that is 5 cm. What is the length of the diagonal of the rectangle?
Solution
We have the following information:
- Base = 12 cm
- Height = 5 cm
We can calculate the diagonal with the formula $latex d= \sqrt{{{a}^2}+{{b}^2}}$. Therefore, we substitute the given values:
$latex d=\sqrt{{{a}^2}+{{b}^2}}$
$latex d=\sqrt{{{12}^2}+{{5}^2}}$
$latex d=\sqrt{144+25}$
$latex d=\sqrt{169}$
$latex d=13$
The diagonal of the rectangle has a length of 13 cm.
EXAMPLE 3
A rectangle has a base of 7 m and a height of 9 m. What is the length of the diagonal of the rectangle?
Solution
We have the values:
- Base = 7 m
- Height = 9 m
The formula for the diagonal of a rectangle is $latex d=\sqrt{{{a}^2}+{{b}^2}}$. Therefore, substituting the given values, we have:
$latex d=\sqrt{{{a}^2}+{{b}^2}}$
$latex d=\sqrt{{{7}^2}+{{9}^2}}$
$latex d=\sqrt{49+81}$
$latex d=\sqrt{130}$
$latex d=11.4$
The diagonal of the rectangle has a length of 11.4 m.
EXAMPLE 4
A rectangle has a base of 15 m and a height of 10 m. What is the length of its diagonal?
Solution
We have the values:
- Base = 15 m
- Height = 10 m
The formula for the diagonal of a rectangle is $latex d= \sqrt{{{a}^2}+{{b}^2}}$. Therefore, using the given information, we have:
$latex d=\sqrt{{{a}^2}+{{b}^2}}$
$latex d=\sqrt{{{15}^2}+{{10}^2}}$
$latex d=\sqrt{225+100}$
$latex d=\sqrt{325}$
$latex d=18.03$
The diagonal of the rectangle is 18.03 m.
EXAMPLE 5
What is the diagonal of a rectangle that has a base of 12 and a height of 20?
Solution
We have the data:
- Base = 12 m
- Height = 20 m
We can use the formula $latex d=\sqrt{{{a}^2}+{{b}^2}}$ with the given values to obtain:
$latex d=\sqrt{{{a}^2}+{{b}^2}}$
$latex d=\sqrt{{{12}^2}+{{20}^2}}$
$latex d=\sqrt{144+400}$
$latex d=\sqrt{544}$
$latex d=23.3$
The diagonal of the rectangle is 23.3 m.
Diagonal of a rectangle – Practice problems
Put into practice what you have learned about the diagonal of a rectangle to solve the following problems. If you need help with these exercises, you can look at the solved examples above.
See also
Interested in learning more about rectangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
