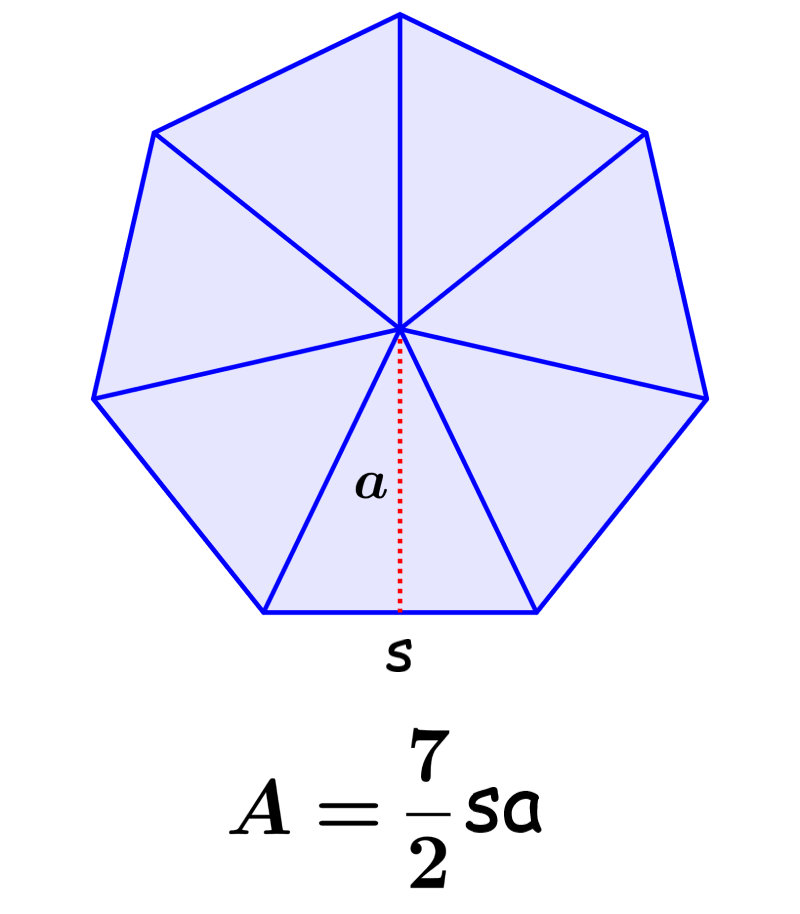
The area of a heptagon is the region enclosed by the seven sides of the heptagon. On the other hand, the perimeter is the sum of all its sides. The area of a heptagon can be calculated using the length of the apothem and the length of the sides, or simply using the length of the sides.
Here, we will look at the main formulas used to calculate the area and the perimeter of a heptagon. Also, we will apply these two formulas to find the solution to some exercises.
How to find the perimeter of a heptagon?
The perimeter of any figure is calculated by adding the lengths of all the sides. In the case of a heptagon, we have to add the lengths of the seven sides, so we have the following formula:
$latex p=a+b+c+d+e+f+g$
where, $latex a, ~b, ~c, ~d, ~e, ~f, ~g$ are the lengths of the sides of the heptagon.
If we have a regular heptagon, we know that the seven lengths are equal, so the formula becomes:
| $latex p=7a$ |
where a is the length of one of the sides of the heptagon.
How to find the area of a heptagon?
To calculate the area of a heptagon, we can use two main formulas, depending on the type of information we have available.
It is possible to use a formula to calculate the area of regular heptagons using the apothem and one of the sides, or simply using the length of one of the sides.
Finding the area of a heptagon using the apothem and sides
Recall that the apothem is the length of the center of the heptagon that is perpendicular to one of its sides. If we divide a heptagon into seven triangles, we have the following figure:
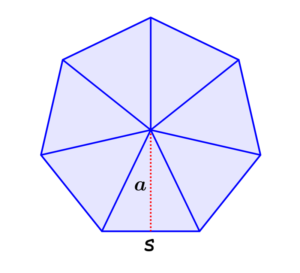
We see that the apothem is equal to the height of one of the small triangles. Also, we know that the area of any triangle is equal to one-half of the base times the height of the triangle.
In this case, the area of each triangle is $latex A=\frac{1}{2}sa$, where, a is the apothem and s is the length of one of the sides. Since we have seven triangles, the area of the heptagon is:
| $latex A=\frac{7}{2}sa$ |
Finding the area of a heptagon using only the length of the sides
If we only know the length of one side of the heptagon, we can use the following formula to calculate the area:
| $latex A=\frac{7}{4}{{s}^2}\cot(\frac{180^{\circ} }{7})$ |
This formula can be simplified by calculating the value of the cotangent and multiplying by the value of the fraction:
| $latex A=3.634{{s}^2}$ |
Area and perimeter of a heptagon – Examples with answers
EXAMPLE 1
What is the perimeter of a heptagon that has sides of length 6 m?
Solution
We can use the perimeter formula with $latex a=6$. Therefore, we have:
$latex p=7a$
$latex p=7(6)$
$latex p=42$
The perimeter of the heptagon is 42 m.
EXAMPLE 2
A heptagon has an apothem of length 4.15 m and sides of length 4 m. What is its area?
Solution
We have the following lengths:
- Apothem, $latex a=4.15$ m
- Sides, $latex s=4$ m
Using the first formula with these values, we have:
$latex A=\frac{7}{2}sa$
$latex A=\frac{7}{2}(4)(4.15)$
$latex A=58.1$
The area of the heptagon is 58.1 m².
EXAMPLE 3
A heptagon has sides of length 11 m. What is its perimeter?
Solution
We have to use the perimeter formula with $latex a=11$. Therefore, we have:
$latex p=7a$
$latex p=7(11)$
$latex p=77$
The perimeter of the heptagon is 77 m.
EXAMPLE 4
What is the area of a heptagon that has an apothem of length 6.23 m and sides of length 6 m?
Solution
We have the following values:
- Apothem, $latex a=6.23$ m
- Sides, $latex l=6$ m
We can use the first formula with these values:
$latex A=\frac{7}{2}sa$
$latex A=\frac{7}{2}(6)(6.23)$
$latex A=130.8$
The area of the heptagon is 130.8 m².
EXAMPLE 5
What is the perimeter of a heptagon that has sides of length 23 m?
Solution
We use the length $latex a=23$ in the perimeter formula. Therefore, we have:
$latex p=7a$
$latex p=7(23)$
$latex p=161$
The perimeter of the heptagon is 161 m.
EXAMPLE 6
A heptagon has an apothem of length 7.27 m and sides of length 7 m. What is its area?
Solution
We have the following values:
Apothem, $latex a=7.27$ m
Sides, $latex s =7$ m
Substituting these values in the first formula, we have:
$latex A=\frac{7}{2}la$
$latex A=\frac{7}{2}(7)(7.27)$
$latex A=178.1$
The area of the heptagon is 178.1 m².
EXAMPLE 7
A heptagon has a perimeter of 49 m. What is the length of its sides?
Solution
In this case, we start with the perimeter and want to find the length of one of the sides. We use the perimeter formula with $latex p=49$ and solve for a:
$latex p=7a$
$latex 49=7a$
$latex a=7$
The length of one of the sides is 7 m.
EXAMPLE 8
A heptagon has sides of length 11 m. What is its area?
Solution
In this case, we only have the length of one of the sides of the heptagon, so we have to use the second formula. To make it easier, we can use the simplified version:
$latex A=3.636{{s}^2}$
$latex A=3.636{{(11)}^2}$
$latex A=3.636(121)$
$latex A=440$
The area of the heptagon is 440 m².
EXAMPLE 9
What is the length of the sides of a heptagon that has a perimeter of 147 m?
Solution
Similar to the previous problem, we use the perimeter formula with $latex p=147$ and solve for a:
$latex p=7a$
$latex 147=7a$
$latex a=21$
The length of the sides of the heptagon is 21 m.
EXAMPLE 10
What is the area of a heptagon that has sides of length 21 m?
Solution
Again, we are going to use the second formula and use the value $latex s=21$:
$latex A=3.636{{s}^2}$
$latex A=3.636{{(21)}^2}$
$latex A=3.636(441)$
$latex A=1603.5$
The area of the heptagon is 1603.5 m².
Area and perimeter of a heptagon – Practice problems
What is the area of a heptagon that has sides of length 16 m?
Write the answer using a single decimal.
See also
Interested in learning more about heptagons? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
