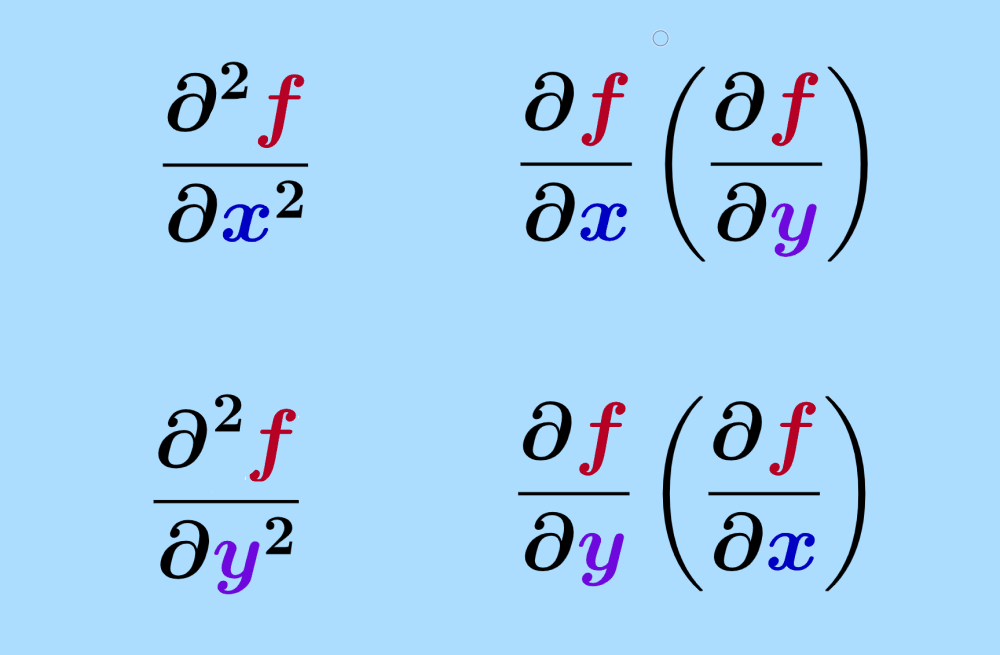Second-order partial derivatives describe the rate at which the partial derivative itself changes with respect to its variables. This information is fundamental to understanding complex systems, from the flow of heat across a surface to the behavior of economic markets.
In this article, we will explore the concept of second-order partial derivatives. We will learn how they are calculated and we will see some practice exercises.
How to calculate second-order partial derivatives?
Second-order partial derivatives are found by calculating the partial derivative of a function twice with respect to the given variables.
For example, if we have the function $latex z=f(x, y)$, then:
$latex \dfrac{\partial^2{f}}{\partial{x^2}}=\dfrac{\partial }{\partial{x}}\left(\dfrac{\partial f}{\partial x}\right)~$ and $latex \dfrac{\partial^2{f} }{\partial x^2}=\dfrac{\partial }{\partial{x}}\left(\dfrac{\partial f}{\partial x}\right)~$
These derivatives can also be written as $latex f_{xx}$ and $latex f_{yy}$, which is subscript notation.
Second-order partial derivatives do not necessarily have to be always with respect to the same variable. We can also calculate mixed partial derivatives:
$latex \dfrac{\partial^2{f}}{\partial x\partial y}=\dfrac{\partial }{\partial{x}}\left(\dfrac{\partial f}{\partial y}\right)~$ and $latex \dfrac{\partial^2{f}}{\partial y \partial x}=\dfrac{\partial }{\partial{y}}\left(\dfrac{\partial f}{\partial x}\right)~$
These derivatives are denoted as $latex f_{xy}$ and $latex f_{yx}$ respectively.
Note: As we will see in the exercises below, it turns out that $latex f_{xy}=f_{yx}$ is always true.
If you need to review first-order partial derivatives, you can visit this article.
Solved exercises of second-order partial derivatives
EXAMPLE 1
Find the derivative $latex \dfrac{\partial^2{f} }{\partial x^2}$ for the following function:
$$f(x, y) = 3x^2 + 4xy + y^2$$
Solution
To calculate this derivative, we have to differentiate the given function twice with respect to $latex x$, while the variable $latex y$ is kept constant.
Then, the first order partial derivative with respect to $latex x$ is:
$$\dfrac{\partial{d}f}{\partial x}=6x+4y$$
By differentiating the term $latex 3x^2$ with respect to $latex x$, we have $latex 6x$. By differentiating the term $latex 4xy$ with respect to $latex x$, we have $latex 4y$.
The derivative of $latex y^2$ with respect to $latex x$ is zero, since the variable $latex y$ is kept constant.
Now, we differentiate $latex \dfrac{\partial f}{\partial x}$ with respect to $latex x$:
$$\dfrac{\partial^2{f}}{\partial x^2}=6$$
EXAMPLE 2
What is the derivative $latex \dfrac{\partial^2{f}}{\partial y^2}$ for the following function?
$$f(x, y) = 3x^2 + 4xy + y^2$$
Solution
In this case, we will differentiate the given function twice with respect to $latex y$, while the variable $latex x$ is kept constant.
Then, differentiating the function with respect to $latex y$, we have:
$$\dfrac{\partial f}{\partial y}=4x+2y$$
The term $latex 3x^2$ is constant, so its derivative is zero.
Now, we can calculate the $latex \dfrac{\partial f}{\partial y}$ with respect to $latex y$:
$$\dfrac{\partial^2{f} }{\partial y^2}=2$$
EXAMPLE 3
Find the derivatives $latex f_{xy}$ and $latex f_{yx}$ of the following function:
$$f(x, y) = 3x^2 + 4xy + y^2$$
Solution
To solve this exercise, we have to calculate the partial derivatives of the function both with respect to $latex x$ and with respect to $latex y$:
$latex f_{x}=6x+4y$
$latex f_{y}=4x+2y$
Now, we find the second-order derivative of $latex f_{x}$ and $latex f_{y}$ with respect to the other variable:
$latex f_{xy}=4$
$latex f_{yx}=4$
We see that the derivative obtained is the same. The equality $latex f_{xy}=f_{yx}$ is always true.
EXAMPLE 4
Find the second-order partial derivatives of
$latex f(x, y) = x^3y + x^2y^2$
Solution
To begin, we find the first-order partial derivatives:
$$f_{x} = 3x^2y + 2xy^2$$
$$f_{y} = x^3 + 2xy$$
Then, we differentiate each of these first-order partial derivatives with respect to the same variable and the other variable:
$latex f_{xx} = 6xy + 6x^2$
$latex f_{xy} = 3x^2 + 4xy$
$latex f_{yx} = 3x^2 + 4xy$
$latex f_{yy} = 2x$
EXAMPLE 5
Find the four second-order partial derivatives of
$latex f(x, y)=x^2+xy^3-y^2$
Solution
To find the four second-order partial derivatives, we have to start by calculating the two first-order partial derivatives:
$latex f_{x}=2x+y^3$
$latex f_{y}=3xy^2-2y$
Now, we can differentiate each of these expressions with respect to $latex x$ and $latex y$:
$latex f_{xx}=2$
$latex f_{xy}=3y^2$
$latex f_{yx}=3y^2$
$latex f_{yy}=6xy-2$
EXAMPLE 6
Find the second-order partial derivatives of the following function:
$latex f(x, y) = x^3y^2 – 2x^2y + 5xy^3$
Solution
First, we find the first-order partial derivatives with respect to $latex x$ and with respect to $latex y$:
$latex f_{x} = 3x^2y^2 – 4xy + 5y^3$
$latex f_{y} = 2x^3y – 2x^2 + 15xy^2$
Then, we differentiate each of these first-order partial derivatives with respect to both variables:
$latex f_{xx} = 6xy^2 – 4$
$latex f_{xy} = 6x^2y-4x + 15y^2$
$latex f_{yx} = 6x^2y-4x+15y^2$
$latex f_{yy} = 2x^3 + 30xy$
EXAMPLE 7
We have the function $latex f(x, y)= ax^2+by^2$, where $latex a$ and $latex b$ are constants.
Find the relationship between $latex a$ and $latex b$ such that $latex f_{xx}+f_{yy}=0$.
Solution
To solve this problem, we start by finding the first-order partial derivatives:
$latex f_{x}=2ax$
$latex f_{y}=2by$
Now, we can calculate the partial derivatives $latex f_{xx}$ and $latex f_{yy}$:
$latex f_{xx}=2a$
$latex f_{yy}=2b$
This means that we have:
$latex f_{xx}+f_{yy}=2a+2b$
We want this to be equal to 0, so we have $latex b=-a$. Therefore, the original function can be written as:
$latex f(x,y)=a(x^2-y^2)$
EXAMPLE 8
Find the four second-order partial derivatives of the following function:
$latex f(x, y) = \sin(x)\cos(y)$
Solution
The first-order partial derivatives are:
$latex f_{x} = \cos(x)\cos(y)$
$latex f_{y} = -\sin(x)\sin(y)$
Then, we derive each of these first-order partial derivatives with respect to both variables:
$latex f_{xx} = -\sin(x)\cos(y)$
$latex f_{xy} = -\cos(x)\sin(y)$
$latex f_{yx} = -\cos(x)\sin(y)$
$latex f_{yy} = -\sin(x)\cos(y)$
Second-degree partial derivatives – Practice problems
Write the answer in the input box.
See also
Interested in learning more about partial derivatives? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
